Dynamic response of auxetic structures

1. Introduction

Auxetic materials are materials that have a negative Poisson’s ratio (they contract or expand in any spatial direction when exposed to a stress), they almost not be found in nature and their behavior emerges from their macro-structure. On a microscopic point of view, they are made from a bulk material of positive Poisson’s ratio.

They have been studied since the late 1980s [1] for their good properties in shock absorption, fracture toughness, indentation resistance and energy dissipation. The auxetic properties often emerge from acute angles in a lattice structure (re-entrant hexagon for example) or spiral geometry.

The geometry presented in this paper is the hexagonal re-entrant structure, one of the most commonly studied [2-7] as it can be defined with very few parameters unlike other more complex structures. This geometry was first invented in 2D but with the development of additive manufacturing was extended to 3D. Samples studied in the literature were usually produced using SLM [8, 9] or other powder bed fusion methods, this produced good quality samples, but at high cost. The advantage of powder bed fusion methods is that the powder supports the structure as it is printed.

The current literature focuses on prediction of the structure’s stiffness, the energy absorption [10], fracture toughness [11] and quasi-static properties [8]. To the author’s knowledge, no study has been proposed that investigates their dynamic response.

This paper will therefore propose modifications on the lattice design to make it easily 3D printable with SLA printers (photo-sensible polymer resin that hardens with UV light). Enabling 3D printing with SLA printers may accelerate research on those structures as samples can be obtained for a very low cost (300 $ printers / 60 $ per liter of resin) and manufactured in any laboratory without specific investment. Their static properties have been investigated and compared to analytical models to assess the generalizability of results. The first requirement to enable SLA based printing methods is that the lattice is self-supporting during manufacture.

We will present a dynamic study of this auxetic structure, studying the influence of two parameters on the lattice frequency response function (FRF): the strut diameter and the mass attached to the sample. Dynamic results are a novelty for auxetic structures so we will initially attempt to use known analytical models to explain the structure’s behavior.

2. Novel structure

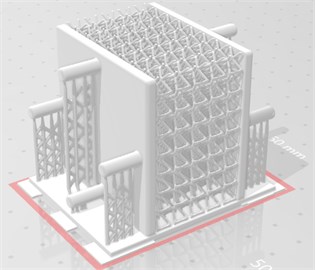
This design varies from the usual design used in previous studies as it has been developed to be 3D printed on an SLA printer. The vertical beams have been modified and are now not flat as shown in Fig. 1.

Thus, they will not be printed in one layer, reducing the overhanging section, a recurrent problem for SLA printers (a non-self-supportive printing technique unlike SLS or SLM). The standard strut design was rectangular on most hexagonal re-entrant structures [12], this novel structure has cylindrical beams which reduces the number of parameters required to fully describe the structure. The vertical beam modification is done via the addition of another beam between the cell corner and a 16th of the angled beam.

As a side effect of the horizontal edge’s modification, the beams junctions are now stronger (the horizontal struts are thicker at their ends). The stress concentrations located at the beam junctions pointed out by Carneiro et al. [13] by an FEA analysis of a 2D hexagonal re-entrant structure can be reduced [4]. This may be an interesting feature to enhance the lattice stiffness and fatigue strength without adding much material and complexity. It does also enable the production of the hexagonal re-entrant structure by SLA printers which is a major improvement as it drastically reduces the cost of production and may help further research on this topic.

Fig. 1Novel lattice design for SLA printing: a) full sample with support, b) single cell

a)

b)

3. Methodology – experimental procedure

Several experimental procedures have been used, two different methods have been developed to measure the frequency response function (FRF) and make sure they were consistent, other tests have been conducted in a tensile/compression bench to evaluate the mechanical properties of the bulk material and the lattice stiffness.

4. Results

4.1. Static tests

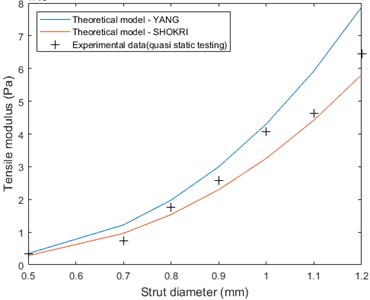
We compared the experimental results to two theoretical models developed by Yang et al. [14] and Shokri et al. [15] that predict the equivalent tensile modulus of an hexagonal re-entrant lattice. The first assumes only two modes of deformation are significant: it uses a Timoshenko beam model to describe the angled beam deformation and a classic compression model for the vertical beam. The second author uses Castigliano’s theorem to calculate the tensile properties, the change in strain energy caused by a force divided by the force itself is equal to the displacement. Note that both methods need to be adapted for cylindrical beams (different cross section area, moment of inertia and Timoshenko beam factor). Although the two approaches are radically different, they give almost similar results as seen in Fig. 2. The novel hexagonal re-entrant structure is comparable to previously studied designs: its mechanical properties can be predicted from the analytical models developed for previous designs.

Fig. 2Compressive tests results comparison to two analytical models

4.2. Dynamic experience – strut diameter influence

From the range of samples produced (7 samples from 0.5 mm strut diameter to 1.2 mm), we observed the FRF and compared them, the results are shown Fig. 3. The frequency response of an auxetic sample has a clear resonance frequency that can be observed in both the amplitude and phase spectrum. The peak width varies linearly with the peak frequency and their width at –3 dB is on average 32 % of the peak frequency.

Fig. 3Strut diameter influence on the FRF

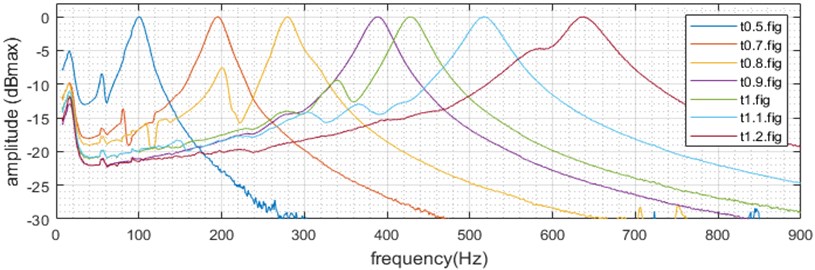
We can see that each sample has a distinct peak corresponding to a resonance phenomenon in the structure, the stiffer the structure, the higher the resonance frequency. We can plot the resonance frequency VS strut diameter as shown in Fig. 4 to see quantitively how the strut diameter affects the dynamic behavior of the structure. We can see a clear linear trend between the resonance frequency and the strut diameter.

Fig. 4Strut diameter influence on the resonance frequency

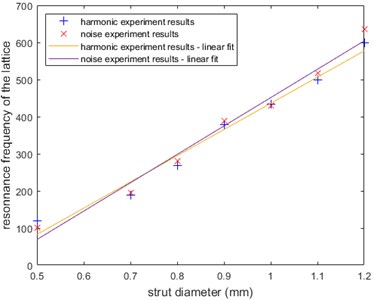
We can first try to explain that trend using a usual linear spring-mass model. As the resonance frequency is $f_{res}=\sqrt{k/m}$ if $k\sim t^2$, we find $f_{res}\sim t$. The second equation can be easily justified as the strut cross sectional area is proportional to $t^2$. This suggests the structure works more in beam compression than in bending (moment of inertia of a beam is proportional to$t^4$). This consideration is however incorrect as Yang et.al analytical model suggests the beam compression is only responsible for 5 to 25 % of the lattice deformation (5 % for $d=$0.5 mm, 25 % for $d=$1.2 mm).

Furthermore, if we calculate $F=\sqrt{k/m}$ with $k$ being the measured static stiffness, we find the right trend but there is a factor ~2 between the calculated resonance frequency and the dynamic experimental results.

4.3. Mass variation

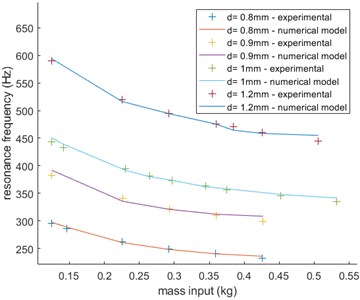
As we saw previously, the linear spring mass model cannot explain the diameter-resonance frequency relationship. We varied the stiffness and observed a discrepancy in the results, in this part, we varied the mass and observed the variation in resonance frequency. Results are presented in Fig. 5 along with the predictions of a non-linear model which we will discuss in the next section. The experiments were conducted for various masses between 124 g (fixation weight) and about 500 g (maximum allowed weight for the shaker).

Fig. 5Mass variation results and non-linear spring model predictions

5. Discussion

The results obtained in section 3.3 cannot be explained by a linear mass-spring model: the variation in resonance frequency does not correspond to any possible prediction of this model if the stiffness is kept constant (for the same sample). If we calculate a “virtual stiffness” for each experiment using $k=f^{2}m$ there is a clear linear relation between this fictional parameter and the mass (with 0 intercept). There is however a model that explains those unusual results almost perfectly as seen in Fig. 5, it is based on a non-linear spring with governing equation $F=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(\mathrm{\Delta }\right)k\text{'}{\mathrm{\Delta }}^4$. The $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(\right)$ function here is used to force $F\left(\mathrm{\Delta }\right)$ to be odd, this equation is therefore not defined the same way for positive and negative deflections. This is one of the reasons why it is simply not possible to solve the governing differential equation of the mass-spring system, the only way to find the resonance frequency is by solving it numerically. We used the ode45() function on MATLAB to simulate the behavior of this non-linear system with 0-initial deflection and acceleration and 1-initial velocity. It is worth noticing that such a system has an unusual behavior and its resonance frequency varies with the initial velocity, the calculated stiffness k’ has therefore no physical sense here as it has been arbitrarily set by choosing an initial velocity of 1 (setting one will force the other parameter during the optimization process to fit the results). To our knowledge there is no theoretical justification that the lattice material behaves like a non-linear material, especially for very small amplitude vibrations. As we saw, this model has however a great predictive power, this unusual dynamic behavior may be due to dissipative effects in the structure’s bulk material that could be non-linear (a viscoelastic model could maybe be used to describe the resin dynamic behavior).

6. Conclusions

A novel structure has been developed with success, it enables 3D printing with SLA printers and has mechanical properties comparable to previously developed structures. It can be described by very few parameters: strut diameter, cell size (the cell fills a cubic volume here, so a single parameter is needed), vertical length ratio and additional strut location parameter (1/16 here) are sufficient to fully describe our novel design. It has been experimentally verified that analytical models developed for previous structures also predict the mechanical properties of our design with good accuracy.

Two dynamic methods have been used to determine FRF of auxetic samples: they give similar amplitude spectrum for different samples which validates them. The results obtained with those method cannot be explained with a simple mass-spring system (sample acting as a linear spring): even though the global trend of the linear system prediction is similar to the of the experimental results, there is an important multiplicative factor between both methods. Furthermore, when we vary the mass attached to the free end of the sample, the change in resonance frequency is not explained by a linear spring model. Even though there is no theoretical justification to the use of a polynomial spring model, it happens that a non-linear spring with governing equation $F=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(\mathrm{\Delta }\right)k{\mathrm{\Delta }}^4$ explains almost perfectly the experimental results. Dissipative effects inside the resin that are not considered in the theoretical models may play a significant role in the dynamic behavior of the sample and be absolutely negligible in quasi-static behavior. This would have to be verified in further studies, which would be highly facilitated by the use of SLA printed samples, which are much easier to produce in significant quantities in a relatively short time and at a moderate cost.