Hysteresis behaviour of different magnetorheological elastomer models: modelling and simulation

1. Introduction

The main goal in vibration control is to eliminate and reduce the vibrations in mechanical systems which also mean that vibration should be isolated from the systems. There are two types of interest namely; force isolation and motion isolation which can be identified from a system with either rotational or linear motion [1]. Base motion isolation is being studied analytically using different models of magnetorheological elastomer (MRE). MRE is a smart composite material that consists of a non-magnetizable polymer matrix embedded with micro/nano-sized ferromagnetic particles. These materials can alter their mechanical properties such as elasticity and stiffness when exposed to an external magnetic field [1, 2]. This property makes them attractive to many engineering applications such as dampers and vibration isolators [3, 4]. The internal magnetic particles which form like a chain in the direction of the magnetic field are the main factor in determining the mechanical properties of these elastomers [4]. Many phenomenological models have been developed to deal with the visco-elastic behaviour of MR dampers described by Hooke’s and Newton’s laws [5]. They are called viscous-elastic materials. Table 1 shows the schematic representations and mathematical models of these models. One of the most used model to describe the viscous-elastic behaviour of MR damper is the Bingham model. It assumes the material to be rigid before yielding [6]. [7] developed a model that shows the hysteretic behaviour of MR damper. Similar to Bouc-Wen model, [7] adopted a 14-parameter model; the modified Bouc-Wen model. This model considers the high non-linear behaviour of MR damper. Dahl model is one of the models developed to describe the behaviour of MR dampers [8]. [9] proposed a new model that utilizes a hyperbolic sine function to represent the hysteresis in order to describe the stiffness and damping characteristics. [10] used MRE as a semi-active vibration isolator to suppress torsional mode of vibration. Results showed that a shift of 3.9 Hz of the natural frequency and slight changes in the damping properties were observed. [11] developed the mathematical and experimental setup for dynamic tuning of torsional vibration; it is found that a shift in the curve was observed in the transmissibility curve (${\theta }_2/{\theta }_1$) as the magnetic field increases.

Table 1Schematic and mathematical representations of different MRE models [7-10]

Schematic representation of models	Mathematical expression by the damping force,$F$
Bingham model	$F=f_{c}sgn\left(\dot{x}\right)+c_0+f_0$ where $f_c$ is the friction force due to yield stress is, $c_0$ is the damping coefficient, $f_0$ is the stored force due to the accumulator
Bouc-Wen model	$F=\alpha z+c_0\dot{x}+k_0(x-x_0)$ $\dot{z}=-\gamma \left|\dot{x}\right|z\left({\left|z\right|}^{n-1}\right)-\beta \dot{x}{\left|x\right|}^n+A\dot{x}$ where $\alpha$ is the scaling Bouc-Wen model parameter related to yield stress of MR damper, $x_0$ is the initial displacement due to effect of the accumulator. $c_0$ and $k_0$ are the damping coefficient and spring stiffness, respectively. $z$ is the deformation of the model due to the hysteretic effect, $\gamma$, $\beta$, $A$ and $n$ are Bouc-wen model parameters
Modified Bouc-Wen model	$F=c_1\dot{y}+k_1\left(x-x_0\right)$ $\dot{y}=\frac{1}{c_0+c_1}[\alpha z+c_0\dot{x}+k_0\left(x-y\right)]$ $\dot{z}=-\gamma \left|\dot{x}-\dot{y}\right|{\left|z\right|}^{n-1}z-\beta \left(\dot{x}-\dot{y}\right){\left|z\right|}^n+A(\dot{x}-\dot{y})$ where $k_1$ is the stiffness of the accumulator, $x_0$ is the initial displacement of spring $k_1$ due to the accumulator effect, $y$ is the internal displacement of the damper, $c_1$ and $c_0$ are the viscous damping coefficients at low and high velocities, respectively. $z$ is an evolutionary variable. $\gamma$, $\beta$, $n$ and $A$ are modified Bouc-wen model parameters
Dahl model	$F=k_{0}x+c_0\dot{x}+\delta z-f_0$ $\dot{z}=\rho (\dot{x}-\left|\dot{x}\right|z)$ where $k_0$ is the stiffness of the spring, $c_0$ is the damping coefficient, $z$ is the intermediate variable and $\rho$ is the coefficient of stiffness
Hysteresis model	$F=c_{0}x+k_0\dot{x}+\alpha z+F_0$ $z=sinh\left(\beta x\right)$ where $F_0$ is the offset of the isolator force, $\beta$ is the scale factor of the displacement of the isolator, $\alpha$ is a factor to scale the hysteresis, and $c_0$ and $k_0$ are the damping coefficient and spring stiffness, respectively

2. Analytical simulations of different MRE models using Matlab

2.1. Mathematical model development and simulation parameters

The purpose of this study is to use MRE in semi-active vibration isolation by which the parameters can be controlled. The system is presented as a simple base motion isolation (base excitation) system by which the excitation input to the base is to be isolated on the mass. This model is developed to represent the MRE mathematically. The mathematical model of the system is a description in terms of equations. Newton’s and conservation of energy are the physical laws as well as the basics in building the model. This system considers one degree of freedom base excitation system as shown in Fig. 1. The system is excited by an input displacement $y\left(t\right)$ applied to the base and an output displacement $x\left(t\right)$ on the mass. Five models are selected from the literature to be modelled and simulated on the base excitation system. MRE properties vary under a magnetic field. Each model has its mathematical representation and equations by which their parameters are a function of a magnetic field; this magnetic field is inputted as an electric current. The simulation is done for each model with and without MRE. When the system is without MRE, it means that the effect of stiffness and damping is not related to the current. For this simulation, the current is varied from 0 A to 4 A.

Fig. 1Schematic representation of base isolation model utilizing MRE

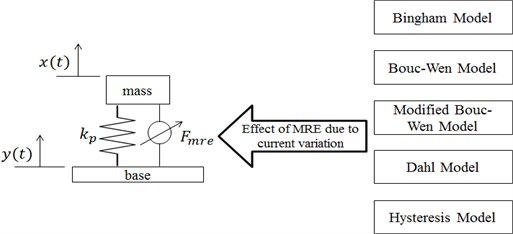
The equation of motion is based on Newton law and it becomes:

1

$\sum F=m\ddot{x},$

2

$m\ddot{x}=-k_p\left(x-y\right)-F_{mre},$

3

$m\ddot{x}+k_{p}x+F_{mre}=k_{p}y.$

Knowing that the force of the MRE is given by:

4

$F_{mre}=k_{mre}\left(x-y\right)+{{[c}_p+c}_{mre}]\left(\dot{x}-\dot{y}\right).$

Then, Eq. (4) becomes:

5

$m\ddot{x}+\left[c_p+c_{mre}\right]\dot{x}+\left[k_p+k_{mre}\right]x=\left[c_p+c_{mre}\right]\dot{y}+\left[k_p+k_{mre}\right]y.$

This is the equation of motion presents the dynamics of the system modelled in terms of $m$, the mass, $y$, the input displacement, $x$, the relative output mass displacement, $c_p$, the passive damping coefficient of MRE when no magnetic field is applied, $c_{mre}$, the active damping coefficient of MRE when the magnetic field is applied, $k_p$, the passive stiffness of MRE when no magnetic field is applied, $k_{mre}$, the active damping coefficient of MRE when the magnetic field is applied. The passive term of the damping coefficient $c_p$ isn’t presented in Fig. 1 and this is due to the fact that its change under magnetic field is not considerable. However, it’s included in the total MRE damping force $F_{mre}$ as in Eq. (4) To simplify the equation, let $k=k_p+k_{mre}$ and $c=c_p+c_{mre}$, Eq. (5) becomes:

6

$m\ddot{x}+c\dot{x}+kx=c\dot{y}+ky.$

The system transfer function can be achieved by taking a Laplace transform to the differential equation by considering the Laplace transform ($a=A\left(s\right)$) on Eq. (6):

7

$m{s}^{2}X\left(s\right)+csX\left(s\right)+kX\left(s\right)=csY\left(s\right)+kY\left(s\right),$

8

$X\left(s\right)\left[m{s}^2+cs+k\right]=Y\left(s\right)\left[cs+k\right],$

9

$\frac{X\left(s\right)}{Y\left(s\right)}=\frac{cs+k}{m{s}^2+cs+k}.$

By using the conversion from ($s$-domain) to ($\omega$- domain) through substituting ($s=j\omega$), the transmissibility factor is given by:

10

$\frac{X\left(j\omega \right)}{Y\left(j\omega \right)}=\frac{cj\omega +k}{m{\left(j\omega \right)}^2+cj\omega +k}.$

By taking the magnitude of Eq. (10) the amplitude of displacement transmissibility is:

11

$T=\left|\frac{X\left(\omega \right)}{Y\left(\omega \right)}\right|=\sqrt{\frac{(c\omega {)}^2+k^2}{(c\omega {)}^2+(k-m{\omega }^2{)}^2}}.$

The mass in this analysis is assumed to be 5 kg. The inputs signals are step input (step time: 0.5, initial value: 0, and final value: 1) and a sinusoidal wave (Amplitude: 1 m, frequency: 10 rad/s). Table 2 below briefly summarizes the five models that will be studied. Also, the mechanical properties of these models of MRE are changeable by applying a current. These relationships with their parameters are also presented which were taken from the literature [8, 12-14]. Some of models parameters are constant and others are field-dependent; by which they depend on the magnetic field which related to the current as shown in Table 2.

Table 2Field-dependency between models parameters and current [8, 12-14]

MRE model	Field-dependent parameters equations
Bingham	$c_0=147.5i+13.52$[N.s/m], $f_c=-394.8i+38.14$[N], $f_0=663.56i+52.19$[N]
Bouc-Wen	$k_0={k_0}_a+{k_0}_{b}i$[N/m], $c_0={c_0}_a+{c_0}_{b}i$[N.s/m], $\alpha ={\alpha }_a+{\alpha }_{b}i$[N/m], $A$, $\beta$, $\gamma$, and$n$ are constants, where ${k_0}_a=$ 469 N/m, ${k_0}_b=$ 323.2 N/m.A, ${c_0}_a=$ 2100 N.s/m, ${c_0}_b=$ 350 N.s/m.A, ${\alpha }_a=$ 14000 N/m, ${\alpha }_b=$69500 N/m.Am, $A=301$, $\beta =$3630000 m-2, $\gamma =$190 s-1 and $n=$ 2
Modified Bouc-Wen	$k_0={k_0}_a+{k_0}_{b}i$ [N/m], $k_1={k_1}_a+{k_1}_{b}i$[N/m], $c_0={c_0}_a+{c_0}_{b}i$ [N.s/m], $c_1={c_1}_a+{c_1}_{b}i$ [N.s/m], $\alpha ={\alpha }_a+{\alpha }_{b}i$ [N/m], $A$, $\beta$, $\gamma$, and $n$ are constants, where ${k_0}_a=$ 500 N/m$$, ${k_0}_b=$ 15.9 N/m.A, ${k_1}_a=$ 469 N/m , ${k_1}_b=$ 323.2 N/m.A, ${c_0}_a=$ 2100 N.s/m, ${c_0}_b=$ 350 N.s/m.A, ${c_1}_a=$ 28300 N.s/m, ${c_1}_b=$ 295 N.s/m.A, ${\alpha }_a=$ 14000 N/m, ${\alpha }_b=$ 69500 N/m.A, $\beta =$3630000 m-2, $A=301$, $\gamma =$190 s-1 and $n=$ 2
Dahl	$k_0={k_0}_a+{k_0}_{b}i$[N/m], $c_0={c_0}_a+{c_0}_{b}i$ [N.s/m], $\delta ={\delta }_a+{\delta }_{b}i$, $\rho$ is constant, where $\rho =$25 kg/m3, $f_0=0.001$, ${k_0}_a=$ 800 N/m, ${k_0}_b=$ 250 N/m, ${c_0}_a=$ 24.64 N.s/m, ${c_0}_b=$ 40.41 N.s/m.A, ${\delta }_a=0.031$, and ${\delta }_b=1.12$
Hysteresis	$c_0={c_0}_a+{c_0}_{b}i$ [N.s/m], $k_0={k_0}_a+{k_0}_{b}i$[N/m], $\alpha ={\alpha }_a+{\alpha }_{b}i$, $\beta$ is constant, where, ${c_0}_a=$ 315.9 N.s/m, ${c_0}_b=$ 2.74 N.s/m.A, ${k_0}_a=$ 246.7 N/m, ${k_0}_b=$ 31.2 N/m.A, ${\alpha }_a=$ 17653 N/m, $F_0=$ 0 N, ${\alpha }_b=$ 1.553 N/m.A, and $\beta =$ 8570000 m-2

The combination of the base isolation system and the damping force by these models is done by combining the equations from Table 1 and Eq. (2). For example, the mathematical expression for this methodology can be given as follows, reconsidering the Bingham model mathematical expression from Table 1, $F=f_{c}sgn\left(\dot{x}\right)+c_0+f_0$, From Eq. (2) for base motion isolation system is:

12

$\ddot{x}=-\frac{k_{p_{Bingham}}}{m}\left(x-y\right)-\frac{F_{mre}}{m}.$

By combining Eq. (1) and Eq. (12), and considering the relative motion between the mass output motion $x\left(t\right)$, and base input excitation $y\left(t\right)$, by which $x=\left(x-y\right)$ and $\dot{x}=\left(\dot{x}-\dot{y}\right)$, Bingham model damping force becomes:

13

$F_{BinghamMR}=f_{c}sgn\left(\dot{x}-\dot{y}\right)+c_0+f_0.$

The combination of Bingham model damping force and the base isolation system becomes:

14

$\ddot{x}=-\frac{k_{p_{Bignham}}}{m}\left(x-y\right)-\frac{1}{m}\left(f_{c}sgn\left(\dot{x}-\dot{y}\right)+c_0+f_0\right).$

The equation in this form is preferable since it’s a second-order differential equation to build the block diagram on Simulink. All models followed the same procedure to be built on Simulink. An example of the combination of equations of these five models can be shown for Bingham model as in Eqs. (22-24). In parallel, the block diagrams are related also to some MATLAB codes developed in order to be simulated. Firstly, the MATLAB code is run for each model which is consists of the field-dependent parameters equations as shown previously in Table 2. Then, the models will be automatically opened and simulated using ‘open’ and ‘sim’ commands in MATLAB. The simulations are done twice for a step input and sinusoidal input with the parameters shown previously. A manual switch is used to connect each input once at a time. Time domains for both inputs are taken as the output of these simulations. Finally, the system with and without MRE are shown in scope and extracted. Stiffness and damping coefficient of each model in the system was calculated from the 2nd order underdamped step responses. All of the five MRE models are summed up as sub-systems so that simulations are done in at the same time.

3. Analytical results and discussion

Stiffness and damping coefficients values are plotted with respect to the applied current, as shown in Figs. 2, 3. It can be clearly seen from Fig. 2 that the stiffness of the MRE for all models increases significantly when the current is increased. For example, the stiffness increases from 150 N/m to 200 N/m at an applied current 0 A to 1 A, respectively. This shows a 33.3 % increase in the stiffness when the current is applied initially. In contrast, the damping coefficient increases from 13.5 N.s/m to 17.945 N.s/m and an applied current 0 A to 1 A, respectively as shown in Fig. 3. This shows a 26.82 % increase in the damping coefficient. For BW model, the stiffness increases by 78 % when 1 A current is applied, an increase of 42.6 % is obtained.

Fig. 2Stiffness values for each MRE model with respect to the applied current

Fig. 3Damping coefficient values for each MRE model with respect to the applied current

The stiffness shows a rise of 63.5 %, 78 % and 90 % for MBW, Dahl and Hysteresis models, respectively whereas the damping coefficient increased by a percent of 19.5 %, 42.3 % and 43.3 %, respectively. Also, the range of the stiffness values is more than the range of the damping coefficient values. For example, the minimum and maximum values of stiffness for MBW model are 212.32 N/m and 1322.46 N/m whereas damping coefficient values are 14.32 N.m/s and 21.32 N.m/s, respectively. This can be seen for all other models as well. Therefore, an increase in the stiffness and damping coefficient is noted when the current is increased. However, the change in the stiffness of the MRE compared to the damping coefficient is significant. This proves the theory mentioned in the literature by which the stiffness of the MRE varies significantly with the magnetic field, whereas the damping characteristics do not. Although the change in the damping in these simulations still considerable but it can be concluded that the MRE stiffness properties vary more significantly than damping. One reason for the significant change is that the equations relating the model parameters might have some magnetorheological fluids (MRF) characteristics. The damping behaviour of MRF is substantial with a magnetic field unlike MRE.

Fig. 4Displacement transmissibility vs frequency for: a) Bingham model, b) Bouc-Wem model, c) Modified Bouc-Wen model, d) Dahl model, and e) Hysteresis model

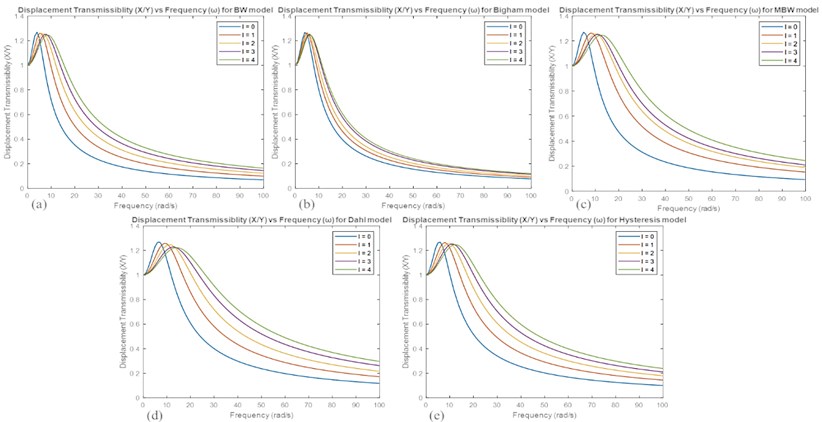
After obtaining $c$ and $k$ values for each MRE model, the transmissibility factor is plotted with respect to the frequency for each model at different current. The range of the frequency for this simulation was set to be 0 H to 100 Hz. It can be clearly seen from Fig. 4 that the natural frequency of the system is increased and the transmissibility curve is shifted to the right. This clearly shows that the curve is being shifted towards the reduction region which means that the vibration is isolated. This shift in the transmissibility curve is evidence showing that the stiffness of the MRE is increased when the applied current increases. In addition, the amplitude is being reduced which means that the damping ratio is increased so that the system is damped better so the vibration is isolated faster. However, as concluded earlier that the change in the damping properties is slighter than the change in the stiffness of the MRE. The transmissibility curve for Bingham model is shifted in a small increment as shown in Fig. 4(a). The variation in the stiffness values is minimum, this due to the simplicity of this model as it has only three parameters related to the current. MBW (Fig. 4(c)) and Dahl (Fig. 4(d)) models show more shifting the transmissibility curve as the applied current increases. This due to the more accurate approximation of the field-dependent parameters that control the hysteresis loops. Altogether, the modelling approach presented in this work is adequate to predict the hysteresis behaviour of different MRE models obtained from the literature. These models were applied on a system subjected to base motion excitation and the transmissibility factor was studied. This study has vast application in vibration isolation. The results given here for the base excitation system will be useful to predict the performance of MRE in vibration isolation applications such engine mounting system.

4. Conclusions

The mathematical model was derived for a base motion isolation system and combined with the mathematical models of five different MREs for step and sinusoidal excitation inputs. It can be concluded from the analytical simulation study that different MRE models were able to reduce vibration in the base isolation system. Bingham, Bouc-Wen, Modified Bouc-Wen, Dahl, and Hysteresis loops were modelled using Simulink and MATLAB. Field-dependent parameters were identified by mathematical expressions. The stiffness and damping coefficients were approximated from the second-order underdamped systems obtained from the step response. It can be clearly deduced that the change in the stiffness for these models is way more than the change in the damping properties. The change in the stiffness was found to be approximately 2 times higher than the change in the damping coefficient which confirms the literature survey. The transmissibility factor was calculated and plotted against a range of frequencies; results showed that there is a shift in the natural frequency of the system for all five models which is due to the change in the stiffness as the applied current is increased. This paper contributed to reviewing different MRE models and studied their performance on the base motion isolation system. The main goal of this study was to test the performance of different MRE models in terms of damping and stiffness properties under an external magnetic field. The transmissibility factor vs excitation frequency was plotted to visualize the efficiency of field-dependent properties in vibration isolation.