Natural frequency analysis of a functionally graded rotor system using three-dimensional finite element method

1. Introduction

A typical functionally graded material (FGM), with a high bending–stretching coupling effect, is an inhomogeneous composite made from different phases of material constituents (usually ceramic and metal). The volume fraction of the constituent materials is gradually varied; thus, the material properties exhibit a smooth and continuous change from one surface to another. Ceramic constituents of FGMs can withstand high-temperature environments due to their better thermal resistance characteristics, while the metal constituents provide stronger mechanical performance and reduce the possibility of fracture. Rotor dynamics analysis of FG rotor forms the base of the current work.

Some of the important works in this direction are presented in the following paragraphs. Nelson and McVaugh [1], presented a procedure for dynamic modeling of rotor-bearing systems which consist of rigid disks and discrete bearings. The formulation was presented in both a fixed and rotating frame of reference. Zori and Nelson [2] study extends the linear finite element concept to provide a detailed evaluation of damped rotor stability. Prabhakar et al [3] worked on crack detection and vibration characteristics of cracked shafts [3]. The works reported in References [1-3] dealt with the dynamic analysis of rotors made of homozeneous isotropic materials.

The first practical application of FGMs was carried out at the National Aerospace Laboratory of Japan in 1984 to prepare advanced ultra-high temperature resistance structural materials [4]. An elasticity solution was provided for FG beams by Sankar [5], using exponential law. Reddy and Chin [6], studied the dynamic thermoelastic response of functionally graded cylinders and plates using finite element modeling and considering the effect of thermomechanical coupling in the formulation. Gayen and Roy [7] work deal with the study of vibration and stability analysis of a functionally graded spinning shaft system using beam elements based on the Timoshenko beam theory.

Most of the previous works in FG systems has been performed using beam elements. As FGM are finding widespread use in industries, analysis using three-dimensional elements for accurate modeling of the problems is necessary. Thus, the present work aims to study the vibration analysis of a shaft and a rotor system, modeled using ANSYS three-dimensional hex elements by considering two different FG materials and temperature distribution laws.

2. Material modelling

To accurately model the properties of FGMs, the properties should be temperature and position dependent. In the case of circular shafts, the radial distribution of properties is present. The temperature-dependent material properties P can be written as in [8] shown in Eq. (1):

where $P_0$,$P_{-1}$, $P_1$, $P_2$, $P_3$are the coefficients of temperature $T$ (in K) and are unique to the constituent materials. Typical values of these constants for material properties like Young’s modulus (in Pa), Poisson’s ratio, thermal expansion coefficient (in K^-1), and the thermal conductivity (in W mK^-1) of ceramics and metals can be obtained from the works of Reddy and Chin 1998 [6]. For a hollow cylinder having temperatures $T_o$ and $T_i$ on outer and inner surface respectively, temperature distribution at any radial distance, $r$ is given by Eq. (2):

The position-dependent material properties $P\left(r\right)$ for a circular FG shaft or cylinder can be expressed by using Eq. (3), [6]. $Pm$ and $Pc$ represents material properties at ceramic rich and metal-rich region respectively as a function of temperature. $Ro$ and $Ri$ are the outer and inner radii of the shaft, respectively. $k$ is the power-law index. NLTD is the solution of Eq. (2), and considering the first seven terms of the polynomial expansion [9], yields Eq. (4). Where $Kcm=Kc–Km$. The density at each layer has been given by Eq. (5):

3. Code validation

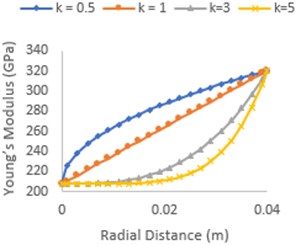
Python code has been developed to generate ANSYS material macros, which can be used to apply the position dependent material properties to a rotor shaft system. To verify the material properties obtained using the developed code, a solid FG shaft composed of Stainless Steel (SS) and Zirconia (ZrO₂) having outer diameter ($Ro$) 100 mm, a ceramic rich region at a temperature of 900 K and metal core at a temperature of 300 K has been considered. The material properties have been calculated at different radial distances, and a graph is plotted for different power-law coefficients ($k$) as shown in Fig. 1. Material properties are validated by the works of Gayen et al. [7]. After validation, the code is extended to different a FG material composed of Al₂O₃ and SUS304 for 80 mm diameter shaft at room temperature. Radial variation of Young’s Modulus from Python output is in good agreement with works of Gayen and Roy [10], which is shown in Fig. 2. Thus, the code is adopted for further works in different FG shaft systems discussed in current work. The points in the plots show the value plotted which lies exactly above the curves obtained from [7, 10].

Fig. 1Young’s modulus variation (SS-ZrO2)

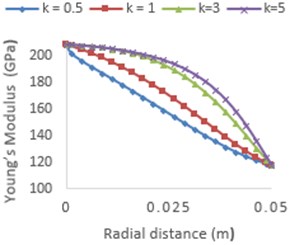
Fig. 2Young’s modulus variation (SS-Al2O3)

4. FE modeling and solution procedure

In the present work, two separate three-dimensional FE models are developed in ANSYS software. The first model is a simply supported FG shaft without disc which is used to validate the FE model with the available literature results. Whereas the second model is an FG shaft supported on bearings and containing a centrally located steel disc. 3-Dimensional 8 noded structural SOLID185 elements having three degrees of freedom per node, have been considered for modeling shaft and disc. The simply supported condition is achieved by fixing displacements in non-axial directions on all nodes present on end faces as shown in Fig. 3. The simply supported FE model is further used to determine the natural frequencies of FG shafts having different material gradations in present work.

Fig. 3Meshed model of simply supported FG Shaft

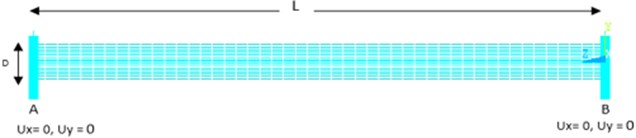
Fig. 4Meshed FE model of rotor bearing system

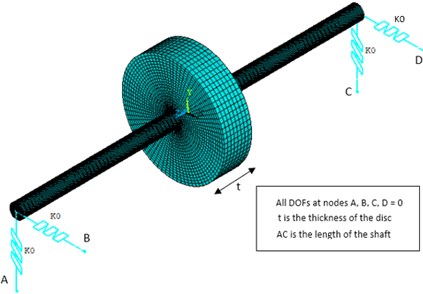
Besides SOLID185 elements, COMBIN 14 elements are used to model the bearings in the second model. COMBIN 14 element takes the bearing stiffness and damping as an input. The displacements at the end nodes of these elements are fixed as shown in Fig. 4 The rotor-bearing model shown in Fig. 4, is used for validation work and has been further used for obtaining the whirl frequencies under different material gradation.

Block Lanczos eigenvalue extraction method is used for obtaining natural frequencies of the simply supported shaft. The whirl frequency extraction of the rotor-bearing system has been carried out using QR damped solver of ANSYS.

5. Results and discussions

A modal analysis of two FE models is performed in ANSYS software to obtain the natural frequencies and mode shapes. Before presenting the results of rotor systems having different material gradations, the developed three-dimensional ANSYS FE models are validated by comparing the modal analysis results (namely the natural frequencies) with works from literature. The validation results are given in the following Sections of 5.1 and 5.2 and further results are presented in Section 5.3 and 5.4.

6. Conclusions

Three-dimensional FE modelling and analysis of the FG rotor systems has been carried out using ANSYS to study the influence of FG material gradation on the natural frequencies. ANSYS macro files are generated using python code which can be read to achieve the layered gradation of material properties.

Power law and NLTD has been used for material gradation and the temperature distribution respectively. Power law coefficients ($k$) have been varied and a decrease in natural frequencies with increasing k values has been observed. Two different FG materials are studied and SS-ZrO₂ shows lower natural frequency at a fixed $k$ value. The whirl frequencies have also been studied, since no significant internal damping, backward whirl has not been observed. Further work is planned on the dynamic analysis of FG rotor system using different FG materials and gradation laws, effect of internal damping and crack inclusion in the shafts.