Liquid induced vibrations of partially liquid-filled elastic cylindrical-conical shells

2.1. Problem statement

Elastic compound shells of revolution, partially filled with liquids, are considered, Fig. 1(a-b). The wetted surface of the shell is denoted as $S_1$, while $S_0$ represents the liquid free surface. It is assumed that the liquid is an ideal and incompressible. Reservoirs consist of coaxial cylindrical and conical shells connected by rings. The liquid is located between the shells. The surfaces of the shells and bottoms are wetted, and the free surface at rest is at a height of $H$, forming a ring, which is described in polar coordinate system as $\left\{z=H,R_1<r<R_0\right\}$. Here for the shell structure, depicted in Fig. 1(a), $R_0=R_3+(R_2-R_3)(L-H)/L$, whereas $R_0=R_3+(R_2-R_3)H/L$ for the shell structure, depicted in Fig. 1(b). The wetted surface $S_1$ consists of cylindrical and conical parts as well as the bottom. The liquid within the shells undergoes vibrations due to applied loads. The resulting flow from these loads is assumed to be irrotational. If $\mathbf{V}\left(V_{\mathit{x}},V_{\mathit{y}},\mathit{}{V}_{\mathit{z}}\right)$ represents the fluid velocity vector, the incompressibility condition of the continuum can be derived from the equation $\mathrm{d}\mathrm{i}\mathrm{v}\mathbf{V}=0$. So, the velocity potential $\mathrm{\Phi }$ can be introduced as $\mathbf{V}=\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{\Phi }$, and it leads to the Laplace equation. The motion governing equations of liquid-filled elastic shells are given by [13]:

where $\mathbf{L}$ and $\mathbf{M}$ denote the operators corresponding to elastic and mass forces acting on the shell structure, $\mathbf{U}=\left(U_1,U_2,U_3\right)$ is the displacement vector, $\mathbf{Q}$ is the vector of external surface loads, and ${\mathbf{P}}_{\mathbf{l}}$ signifies hydrodynamic pressure, ${\mathbf{P}}_{\mathbf{l}}=p\mathbf{n}$.

Fig. 1Сylindrical – conical compound shells and their drafts

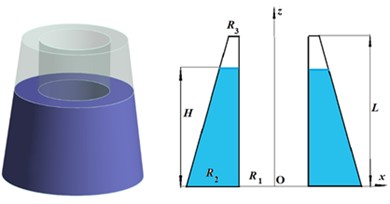
a)

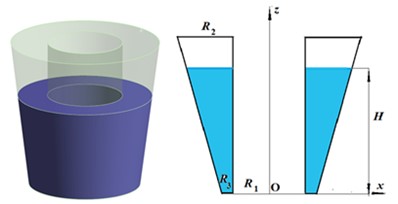
b)

The pressure value $p$, according to the Bernoulli integral, can be represented as $p=-{\rho }_l\frac{\partial \mathrm{\Phi }}{\partial t}{p}_0$, where $p_0$ is atmospheric pressure. The region occupied by the liquid is denoted by $\mathrm{\Omega }$, and $\mathbf{P}$ is for points within $\mathrm{\Omega }$. Boundary conditions for the Laplace equation within $\mathrm{\Omega }$ are outlined as follows. On surfaces $S_1$, no-slip conditions are enforced, and on $S_0$ the dynamic condition is set:

So, it is necessary to determine the unknown functions $\mathrm{\Phi }$ and $\mathbf{U}$ through Eq. (1-2) including boundary and initial data. The unknown vector-function is represented as following series:

where functions ${\mathbf{u}}_k(x,y,z)$ are natural vibration modes of the empty shell structure, and $c_k\left(t\right)$ are time-dependent unknown factors. To determine the vibration modes ${\mathbf{u}}_k(x,y,z)$, the FEM is used [4]. To determine potential $\mathrm{\Phi }$, boundary value problem Eq. (2) is solved. The following series is incorporated $\mathrm{\Phi }\left(r,\theta ,z,t\right)={\sum }_{k=1}^n{\phi }_k\left(r,\theta ,\mathrm{}z\right){\dot{c}}_k\left(t\right).$ Here the functions ${\phi }_k(x,y,z)$ are solutions of boundary value problem Eq. (2) with $\frac{\partial {\phi }_k}{\partial \mathbf{n}}=\left({\mathbf{u}}_k,\mathbf{n}\right)$.

For shells of revolution, all unknown functions for each $l$ can be expressed in the form [4]:

Such presentations simplify the dynamical analysis by reducing the problem to a series of uncoupled single-degree-of-freedom systems, depending on $l$ only.

3.1. Validation

The validation study involves truncated isotropic conical tanks. Let $R_1$ and $R_2$ are the cone radii at its larger and smaller ends, $\alpha$ is the semi-vertex angle, and $H$ is the cone height. In numerical simulations, the shell thickness is $h/R_1=$0.01. The semi-vertex angle is $\alpha =$45°, $H/R_2=$1, $E=$2.11·10⁶MPa, $\nu =$0.3, ${\rho }_s=$8000 kg/m³, ${\rho }_l=$ 1000 kg/m³, and $R_1=$1 m, [16]. Shell edge fixations are clamped–clamped (CC), clamped–simply supported (C-SS), simply supported –clamped (SS-C), and clamped –free (C-F) ones. Convergence was achieved when the number of finite elements on the tank walls equals 30. Table 1 provides comparison of obtained results with data of [16]. The specified above boundary conditions are considered, with wave numbers $l=$ 0, 1,…, 7.

In this comparison, dimensionless frequencies are obtained for truncated isotropic elastic conical tanks for $k=$1, $\alpha =$45°, using the frequency parameter ${\mathrm{\Omega }}_1$ as in [16]. The results obtained by the proposed reduced BEM are in good agreement with data of [16].

3.2. Vibrations of elastic cylindrical-conical shells.

The vibration frequencies and modes of the empty and fluid-filled structures, depicted in Fig. 1, are estimated. The next parameters are chosen: $L=$ 1 m, $R_1=$ 0.5 m, $R_2=$ 0.5 m, $R_3=$0.25 m, the filling level $H=$ 1.25 m. The material and mechanical properties are ${\rho }_s=$7800 kg/m³, $E=$2.1 10⁶ MPa, $\nu =$0.3, the thickness of the shell structure is 3 mm. The structure has been rigidly bottom fixed. The frequencies and modes of the empty structure are calculated first; the FEM [6] is used. Table 2 shows the lowest vibration frequencies of unfilled structures, Fig. 1(a)-(b).

The frequencies of the structure depicted in Fig. 1(b) slightly differ from the frequencies of the structure shown in Fig. 1(a). The corresponding vibration modes ${\mathbf{u}}_{kl}$ are shown in Fig. 2.

Fig. 2Vibration modes of the unfilled structures

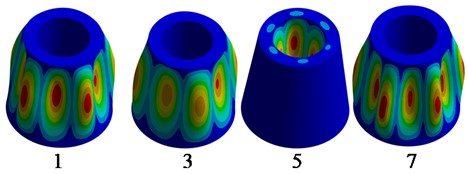
a) Modes of shell structure Fig. 1(a)

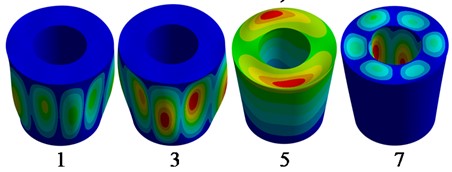
b) Modes of shell structure Fig. 1(b)

Note that, as in [16], the lowest frequencies correspond to 6th and 7th wavenumbers. It should also be noted the presence of practically multiple frequencies. Next, the base functions ${\phi }_k\left(r,\theta ,H\right)$ and the corresponding frequencies are obtained. These functions are vibration modes of the structure walls, considering the liquid added masses. The frequencies are provided in Table 3.

Significant decreasing in frequencies compared to the empty shells has been observed. Multiple frequencies are also available. Fig. 3 depicts some characteristic vibration modes.

The lowest frequency corresponds to the eighth wave number. This result cannot be predicted theoretically, and only computer experiments allow to understand the nature of vibration patterns.

Fig. 3Vibration modes φkr,θ, H of elastic walls considering liquid added masses

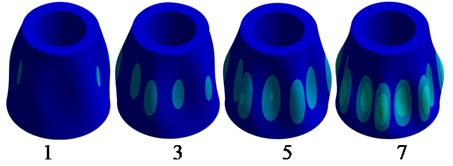
a) Modes of shell structure Fig. 1(a)

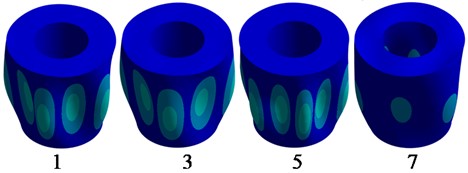
b) Modes of shell structure Fig. 1(b)