Liquid vibrations in a container with a membrane at the free surface

Choudhary, Neelam; Strelnikova, Elena

doi:10.21595/vp.2021.21996

Vibroengineering Procedia

Browse Procedia

Published: 07 May 2021

Check for updates

Liquid vibrations in a container with a membrane at the free surface

Neelam Choudhary¹

Elena Strelnikova²

¹Department of Mathematics, Bennett University, Greater Noida, 201310, India

²A. N. Podgorny Institute of Mechanical Engineering Problems, National Academy of Sciences of Ukraine, Kharkiv, Ukraine

Corresponding Author:

Neelam Choudhary

Cite the article Download PDF

Downloads 833

CrossRef Citations 7

Abstract

In the paper, the vibrations of liquid in a rigid and circular cylindrical container have been investigated. The effects of an elastic membrane placed on the free surface of the fluid have been analyzed on sloshing frequencies. The cylindrical container is assumed to be partially filled with an incompressible fluid. The potential theory is used to formulate the mathematical problem and set up the boundary value problem. The solutions are obtained for velocity potential and the deflection of elastic membrane in form of Fourier-Bessel series. The results are compared for the proposed analytical approach and BEM.

Highlights

An analytical approach is used to solve the boundary value problem.
Sloshing in presence of membrane on liquid free surface is discussed.
Vibrations modes are reported.

1. Introduction

“Sloshing is known as the free surface motion in a tank which is filled partially” [8]. Slosh motion is a potentially dangerous situation to engineering structures and environment and can lead to the failure of structural units and their stability. The dynamic behaviour of structures carrying fuel tanks or storage reservoirs is significantly affected by fluid structure-interaction and is very dangerous to the safety and stability of the structure. It is necessary to control the vibrations of fluid-structure interaction to maintain the stability of the structures used in various engineering applications such as transporting liquid, petroleum reservoirs and space vehicles. Control of fluid sloshing inside a container has always been a challenge while designing any tank due to uninvited vibrations which are dangerous for the stability of the system. The Gas-free liquid is a key function of propellant tanks/containers in spacecraft and offshore oil industry where floating roofed oil tanks are used Propellant sloshing in tanks also influences the rigid body motion of the spacecraft or launch vehicles, which then needs to be controlled by the reaction control system.

Sloshing is a worrisome situation in oil storage tanks as well as in natural gas reservoirs. In recent years, floating liquified natural gas (FLNG) has gained popularity as innovative technology when it comes to natural gas exploitation. These floating platforms as well as huge tanks filled with LNG/ Oil are vulnerable to the vibrations due to ground motion during an earthquake. Suppression devices (rigid/elastic) are considered most effective to dampen the impact loads due to sloshing in a tank as shown in the studies reported in [1-6]. The effects of rigid baffles on sloshing frequencies in circular cylindrical containers are investigated analytically in [1, 2]. The non-linear sloshing problem is reported in [3] and stress analysis is investigated. The effects of vertically placed baffles have been reported in [4] and [6]. Some studied on floating roof (considered as membrane) effects on sloshing frequencies since Tokachi-Oki (2003) earthquake are reported in [7-9], and [12]. The effects of perforated baffles on sloshing are reported in [10] and [11]. The vibrations of liquid in cylindrical tanks with and without baffles on the free surface under horizontal and vertical excitation are reported in [13]. The problem of sloshing in horizontal elliptical tanks with T-shaped baffles is investigated in [14]. Many researchers have been investigating the membrane’s dynamic response due to sloshing. In this paper, the fundamental sloshing modes of liquid with a membrane placed on the free surface are reported.

2. Problem statement

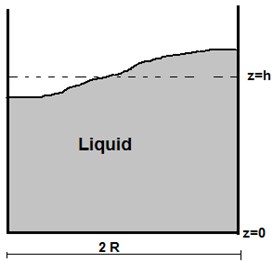
Fig. 1 shows a schematic diagram of sloshing in a container with elastic membrane placed at the free surface. A vertical circular cylindrical tank with radius $R$ containing a fluid free surface at rest is considered at height $h$ from the rigid bottom of the container. To model the sloshing problem, the following assumptions are made: (i) the container is rigid and flow field is considered irrotational, (ii) the fluid is considered incompressible, (iii) small displacement of free surface of liquid are considered. The velocity potential theory is used to formulate the problem. The boundary value problem in terms of the velocity potential is given as follows.

Fig. 1Schematic diagram of the problem

For an irrotational flow motion, the velocity $V$ can be written as a gradient of potential $ϕ (r, θ, z, t)$ such that $V = \nabla ϕ$ . Based on above assumptions of the potential theory, velocity potential satisfies the Laplace equation:

1

\nabla^{2} ϕ = 0, 0 < r < R, 0 \leq θ \leq 2 π, 0 \leq z \leq h .

The boundary conditions at the rigid boundary of the cylinder are at the cylinder wall $r = R$ and at the rigid bottom:

2

z = 0, \frac{\partial ϕ}{\partial r} = 0, \frac{\partial ϕ}{\partial z} = 0 .

The boundary condition for motion of membrane at the free surface is given by:

3

\begin{matrix} \frac{\partial^{2} \bar{w}}{\partial r^{2}} + \frac{1}{r} \frac{\partial \bar{w}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} \bar{w}}{\partial θ^{2}} - \frac{μ}{T} \frac{\partial^{2} \bar{w}}{\partial t^{2}} = - \frac{p}{T}, \end{matrix}

where $\bar{w}$ denotes the deflection of the membrane, $T$ the tension per unit length, $μ$ mass/unit area of the membrane and $p$ denotes the liquid pressure on the membrane. The membrane deflection satisfies the following boundary conditions at the rigid wall of the container $r = R$ :

4

\frac{\partial \bar{w}}{\partial r} = \bar{w} = 0 .

The continuity of normal velocity components at the free surface $z = h$ should be satisfied:

5

\frac{\partial ϕ}{\partial z} = \frac{\partial \bar{w}}{\partial t},

and the dynamic boundary condition at $z = h$ gives:

6

p = - ρ \frac{\partial ϕ}{\partial z} - ρ g \bar{w} .

So, the coupled boundary value problem given by Eqs. (1)-(6), is required to solve to find the unknown functions $ϕ$ and $\bar{w}$ . First, we describe the analytical approach. The separation of variables method is used to find the velocity potential in the following form:

7

ϕ (r, θ, z, t) = \sum_{m = 0}^{\infty} \sum_{n = 1}^{\infty} A_{m n} J_{m} (\frac{k_{m n} r}{R}) c o s h (\frac{k_{m n} z}{R}) c o s m θ e^{i ω t},

where $k_{m n}$ are roots of ${J'}_{m} (k R) = 0$ . Using velocity potential function for Eq. (6), have the expression for pressure can be written as:

8

p = e^{i ω t} [- p i ω \sum_{m = 0}^{\infty} \sum_{n = 1}^{\infty} A_{m n} J_{m} (\frac{k_{m n} r}{R}) c o s (m θ) c o s h (\frac{k_{m n} h}{R})] - ρ g \bar{w} .

The thickness of the membrane is considered negligible. Eq. (4) gives rise to:

9

\frac{\partial^{2} w_{1}}{\partial r^{2}} + \frac{1}{r} \frac{\partial w_{1}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} w_{1}}{\partial θ^{2}} + (\frac{μ {\bar{ω}}^{2} - g ρ}{T}) w_{1} = \frac{i ρ \bar{ω}}{T} \sum_{m = 0}^{\infty} \sum_{n = 1}^{\infty} A_{m n} J_{m} (\frac{k_{m n} r}{R}) c o s (m θ) c o s h (\frac{k_{m n} h}{R}),

which is a nonhomogeneous differential equation in $\bar{w}$ . Solution for the deflection of membrane is following:

10

\bar{w} (r, θ, t) = e^{i ω t} [\sum_{m = 0}^{\infty} \sum_{n = 1}^{\infty} A_{m n} (\frac{i ρ ω R^{2}}{T}) c o s h (\frac{k_{m n} h}{R}) \frac{J_{m} (\frac{k_{m n} r}{R}) c o s m θ}{[c^{2} - k_{m n}^{2}]}

+ \sum_{m = 0}^{\infty} B_{m} J_{m} (\frac{c r}{R}) c o s m θ], c^{2} = \frac{μ ω^{2} - ρ g}{T} .

Using Eq. (5) at $z = h$ , we obtain:

11

\sum_{m = 0}^{\infty} \sum_{n = 1}^{\infty} A_{m n} \frac{k_{m n}}{R} J_{m} (\frac{k_{m n} r}{R}) s i n h (\frac{k_{m n} h}{R}) c o s m θ

= {(i ω)}^{2} \times [\sum_{m = 0}^{\infty} \sum_{n = 1}^{\infty} \frac{i ω R^{2}}{T} A_{m n} J_{m} (\frac{k_{m n} r}{R}) c o s h (\frac{k_{m n} h}{R}) \frac{c o s m θ}{[c^{2} - {k^{2}}_{m n}]}] \times \sum_{m = 0}^{\infty} B_{m} J_{m} (\frac{k_{m n} r}{R}) c o s m θ .

Boundary condition $w =$ 0, at $r = R$ gives:

12

\sum_{m = 0}^{\infty} \sum_{n = 1}^{\infty} A_{m n} (\frac{i ρ ω R^{2}}{T}) \frac{J_{m} (k_{m n}) c o s m θ}{[c^{2} - k_{m n}^{2}]} c o s h (\frac{k_{m n} h}{R}) + \sum_{m = 0}^{\infty} B_{m} J_{m} (c) c o s m θ = 0 .

To determine the unknowns $A_{m n}$ , $B_{m}$ and unknown frequency $\bar{ω}$ , given by the Eqs. (11) and (12) is tedious task. This problem was solved using method developed in [1, 2]. For simulations using BEM, first we consider the problem of free vibrations of membrane without interaction with the liquid. We have:

13

\frac{\partial^{2} \bar{w}}{\partial r^{2}} + \frac{1}{r} \frac{\partial \bar{w}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} \bar{w}}{\partial θ^{2}} - \frac{μ}{T} \frac{\partial^{2} \bar{w}}{\partial t^{2}} = 0,

with $\frac{\partial \bar{w}}{\partial r} = \bar{w} = 0$ .

Supposing that $\bar{w} = w_{1} (r, θ) e^{i \bar{ω} t}$ , one can obtain:

14

L [w_{1}] + {\bar{ω}}^{2} \frac{μ}{T} w_{1} = 0, L [w_{1}] = \frac{\partial^{2} w_{1}}{\partial r^{2}} + \frac{1}{r} \frac{\partial w_{1}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} w_{1}}{\partial θ^{2}}

The solutions of this problem are own modes and own frequencies, ${\bar{ω}}_{m k},$ $w_{1 m k} = w_{m k} (r) c o s m θ$ .

These modes and frequencies are reported in [14]. To obtain the solution of coupled problem the next series is used for each $m$ :

15

\bar{w} (r, θ, z, t) = c o s m θ \sum_{k = 1}^{N_{w}} c_{k} (t) w_{m k} (r) .

Then the next representation for function $ϕ$ is obtained:

16

ϕ (r, θ, z, t) = c o s m θ \sum_{k = 1}^{N_{w}} {\dot{c}}_{k} (t) {\bar{Φ}}_{m k} (r) .

We obtain the system of ODEs of second order for each $m$ in the following form:

17

A^{m} \ddot{C} + B^{m} C = 0,

where:

C = {\{c_{k} (t)\}}_{k = 1}^{N_{1}}, A^{m} = {\{A_{k l}^{m}\}}_{k, l = 1}^{N_{1}}, B^{m} = {\{B_{k l}^{m}\}}_{k, l = 1}^{N_{1}},

A_{k l}^{m} = \frac{μ}{T} (w_{m k}, w_{m l}) + ρ ({\bar{Φ}}_{m k}, w_{m l}), B_{k l}^{m} = ({\bar{ω}}_{m k}^{2} + ρ g) (w_{m k}, w_{m l}) .

For receiving functions ${\bar{Φ}}_{m k}$ the boundary element method is in used [13]. If we suppose that $c_{k} (t) = e x p (i ω t)$ , we get the eigenvalue problem. We will seek the harmonic functions ${\bar{Φ}}_{m k}$ in the form of the sum of simple and double layer potentials [16].

We shall indicate a moistened surface of a shell through $S_{1}$ . The free surface of the liquid $S_{0}$ coincides with the plane $x y (o r r, θ)$ in unperturbed state. So, we have the singular integral equations for receiving ${\bar{Φ}}_{m k}$ in the following form:

18

2 π \bar{Φ} (P_{0}) + \iint_{S_{1}} \bar{Φ} \frac{\partial}{\partial n} \frac{1}{|P - P_{0}|} d S_{1} = \iint_{S_{0}} w \frac{1}{|P - P_{0}|} d S_{0} .

This equation is reduced to one-dimensional one as in [15]. For numerical simulation, the boundary elements with constant density are applied. Here, $N_{0}$ is the number of boundary elements along the free surface radius; $N_{w}$ along the shell wall, and $N_{b o t}$ along the shell bottom. Consider the rigid circular cylindrical shell with the radius and height as $R =$ 1 m, and $h =$ 1 m, respectively. Table 1 below provides the numerical values of the natural frequencies of liquid sloshing for $m =$ 1.

Table 1Slosh frequency parameters ωmk2/g of the fluid-filled rigid cylindrical shell

$m$	BEM			$k =$ 1	$k =$ 2	$k =$ 3	$k =$ 4	$k =$ 5
1	$N_{0}$	$N_{w}$	$N_{b o t}$	$k =$ 1	$k =$ 2	$k =$ 3	$k =$ 4	$k =$ 5
	25	20	20	1.6590	5.3301	8.5385	11.7071	14.8684
	50	40	40	1.6579	5.3297	8.5372	11.7082	14.8655
	100	80	80	1.6573	5.3293	8.5366	11.7066	14.8635
	Analytical solution			1.6573	5.3293	8.5363	11.7060	14.8635

The results of Table 1 testify convergence of proposed BEM. In should be noted that the accuracy $ε =$ 10^-4 has been achieved here for $N_{0} = N_{w} = N_{b o t} =$ 80.

3. Results

Several numerical experiments have been performed to validate the accuracy of the proposed analytical method and determine the frequency. Eqs. (11) and (12) are solved to determine frequencies $ω$ .

Table 2Validation of numerical and analytical results

Frequency (Hz)	1	2	3	4
Method	1	2	3	4
BEM, 40 Elements	0.95582	1.62832	2.05986	2.41284
Analytical Solution	0.95597	1.62777	2.05970	2.41198

The validation of numerical results using BEM with the deployed analytical approach is shown in Table 2. The results show a good convergence. For computations, the parameters of clamped Silicon membrane are considered as the following: $R =$ 0.5 m, $ρ =$ 998 kg/m³, thickness $h_{m} =$ 0.001 m, material density $ρ_{m} =$ 2800kg/m³, Young modulus $E =$ 50 MPa, Poison’s ratio $v =$ 0.49, and $h =$ 1 m. Fundamental modes of sloshing of liquid vibrations are shown in Fig. 2.

Fig. 2Fundamental slosh modes of liquid in a circular cylindrical container

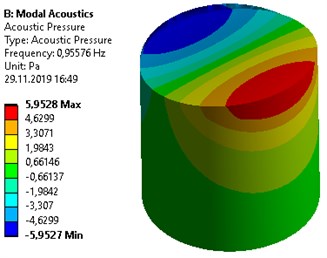
Fig. 3Sloshing modes with membrane vibrations as Eva plastic roof on free surface

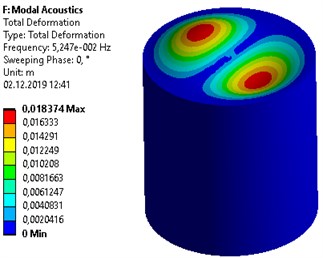
To see the modes of membrane, Eva plastic membrane is used at the free surface. The radius of the membrane is taken with 0.5 m, thickness $h_{m} =$ 0.001 m, material density as 950 kg/m³. The sloshing modes of the membrane are shown in Fig. 3.

4. Conclusions

In this paper, the sloshing in a right vertical circular cylindrical container in the presence of a membrane placed at the free surface is investigated. The fundamental sloshing modes of liquid with and without membrane at the free surface are reported. An analytical approach used to determine sloshing frequencies is validated using Boundary Element Method (BEM). A good agreement is shown between two, even for a small number of boundary elements. The main aim of this research was to validate both analytical and numerical methods using comparison of the results.

References

Choudhary N., Bora S. N. Liquid sloshing in a circular cylindrical container containing a two-layer fluid. International Journal of Advances in Engineering Sciences and Applied Mathematics, Vol. 8, Issue 4, 2016, p. 240-248.

Publisher
Choudhary N., Bora S. N. Linear sloshing frequencies in the annular region of a circular cylindrical container in presence of a rigid baffle. Sadhana-Academy Proceedings in Engineering Sciences, Springer, Vol. 42, Issue 5, 2017, p. 805-815.

Publisher
Falahaty H., Khayyer A., Gotoh H. Enhanced particle method with stress point integration for simulation of incompressible fluid-nonlinear elastic structure interaction. Journal of Fluids and Structures, Vol. 81, 2018, p. 325-360.

Publisher
George A., Cho I. H. Anti sloshing effects of a vertical porous baffle in a rolling rectangular tank. Ocean Engineering, Vol. 214, 2020, p. 107871.

Publisher
Gotoh H., Khayyer A. On the state of the art of particle methods for coastal and ocean engineering. Coastal Engineering Journal, Vol. 60, Issue 1, 2018, p. 79-103.

Publisher
Goudarzi M. A., Danesh P. N. Numerical investigation of a vertically baffled rectangular tank under seismic excitation. Journal of Fluids and Structures, Vol. 61, 2018, p. 450-460.

Publisher
Hosseini M., Goudarzi M. A., Soroor Reduction of seismic sloshing in floating roof liquid storage tanks by using a suspended annular baffle (SAB). Journal of Fluids and Structures, Vol. 71, 2017, p. 40-55.

Publisher
Ibrahim R. A. Liquid sloshing dynamics: theory and applications. Cambridge University Press, p. 970, 2005.

Publisher
Koh C. G., Luo M., Gao M., Bai W. Modelling of liquid sloshing with constrained floating baffle. Computers and Structures, Vol. 122, 2013, p. 270-279.

Publisher
Molin B., Remy F. Experimental and Numerical Study of the sloshing motion in a rectangular tank with a perforated screen. Journal of Fluids and Structures, Vol. 43, 2013, p. 463-480.

Publisher
Molin B., Remy F. Inertia effects in TLD sloshing with perforated screens. Journal of Fluids and Structures, Vol. 59, 2015, p. 165-177.

Publisher
Sakai F., Inouse R. Some considerations on seismic design and controls of sloshing floating roofed oil tanks. The 14th World conference on Earthquake Engineering, 2008.

Search CrossRef
Strelnikoiva E., Choudhary N., Denis V., Krivtchenko, Vasyl Gnitko I., Tonkonozhenko Anatoly M. Liquid vibrations in circular cylindrical tanks with and without baffles under horizontal and vertical excitations. Engineering Analysis with Boundary Elements, Vol. 120, 2020, p. 13-27.

Publisher
Kolaei A., Rakheja S. Free vibration analysis of coupled sloshing-flexible membrane system in a liquid container. Journal of Vibration and Control, Vol. 25, Issue 1, 2019, p. 84-97.

Publisher
Gnitko V., Degtyariov K., Karaiev A., Strelnikova E. Multi-domain boundary element method for axisymmetric problems in potential theory and linear isotropic elasticity. WIT Transactions on Engineering Sciences, Vol. 122, 2019, p. 13-25.

Publisher
Brebbia C. A., Telles J. C. F., And Wrobel L. C. Boundary Element Techniques. Springer-Verlag, Berlin and New York, 1984.

Publisher

Cited by

Liquid induced vibrations of partially liquid-filled elastic cylindrical-conical shells

Neelam Choudhary | Kirill Degtyarev | Elena Strelnikova | Saurabh Rana

(2024)

Numerical study on sloshing in coaxial shells

Neelam Choudhary | Saurabh Rana | Kirill Degtyarev | Denys Kriutchenko | Elena Strelnikova

(2024)

Membrane installation in storage tanks for seismic loads impact protection

Olena Sierikova | Elena Strelnikova | Denys Kriutchenko

(2023)

Sloshing reduction in three-dimensional rectangular container using rigid baffles

Narveen Kumar | Neelam Choudhary

(2022)

Sloshing mitigation using vertical cylindrical baffle

Narveen Kumar | Neelam Choudhary

(2022)

2021 International Conference on Recent Advances in Mathematics and Informatics (ICRAMI)

Neelam Choudhary

(2021)

2021 International Conference on Recent Advances in Mathematics and Informatics (ICRAMI)

Narveen Kumar | Neelam Choudhary

(2021)

About this article

Received

13 April 2021

Accepted

29 April 2021

Published

07 May 2021

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/vp.2021.21996

Keywords

sloshing

vibration

membrane

cylindrical container

Acknowledgements

The authors acknowledge the support of the Indo-Ukraine Joint Research Project Grant funded by DST, India, and Education and Science Ministry of Ukraine.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 04 04

Liquid induced vibrations of partially liquid-filled elastic cylindrical-conical shells

Neelam Choudhary, Kirill Degtyarev, Elena Strelnikova, Saurabh Rana

Research article

2022 10 22

Sloshing mitigation using vertical cylindrical baffle

Narveen Kumar, Neelam Choudhary

Research article

2022 05 16

Sloshing reduction in three-dimensional rectangular container using rigid baffles

Narveen Kumar, Neelam Choudhary

Research article

2020 11 07

Seismic responses of concrete rectangular liquid storage structure with large height-width ratio

Wei Jing, Shangshang Xing, Yu Song

N. Choudhary and E. Strelnikova, “Liquid vibrations in a container with a membrane at the free surface,” Vibroengineering PROCEDIA, Vol. 37, pp. 13–18, May 2021, https://doi.org/10.21595/vp.2021.21996

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2021.21996
UR  - https://doi.org/10.21595/vp.2021.21996
TI  - Liquid vibrations in a container with a membrane at the free surface
T2  - Vibroengineering PROCEDIA
AU  - Choudhary, Neelam
AU  - Strelnikova, Elena
PY  - 2021
DA  - 2021/05/07
PB  - JVE International Ltd.
SP  - 13-18
VL  - 37
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Choudhary_2021,
	doi = {10.21595/vp.2021.21996},
	url = {https://doi.org/10.21595/vp.2021.21996},
	year = 2021,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {37},
	pages = {13--18},
	author = {Neelam Choudhary and Elena Strelnikova},
	title = {Liquid vibrations in a container with a membrane at the free surface},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]N. Choudhary and E. Strelnikova, “Liquid vibrations in a container with a membrane at the free surface,” Vibroengineering PROCEDIA, vol. 37, pp. 13–18, May 2021, doi: 10.21595/vp.2021.21996.

Copy IEEE

Copied to clipboard!

Choudhary, Neelam, and Elena Strelnikova. “Liquid Vibrations in a Container with a Membrane at the Free Surface.” Vibroengineering PROCEDIA 37 (May 7, 2021): 13–18. https://doi.org/10.21595/vp.2021.21996.

Copy Chicago

Copied to clipboard!

Liquid vibrations in a container with a membrane at the free surface

Abstract

Highlights

1. Introduction

2. Problem statement

3. Results

4. Conclusions

References

Cited by

About this article

Related Articles