Abstract
In single crystal diamond tool grinding, cutting-edge quality is affected by various parameters, with tool vibration playing a crucial role. Due to environmental factors and the complexity of the process, vibration signals are often noisy and non-stationary. This study proposes a denoising method that optimizes the wavelet threshold function using an Improved Genetic Algorithm (IGA). The method introduces a configurable value α in the wavelet threshold function, which is optimized with IGA to improve denoising. MATLAB R2018b simulations show that this approach achieves better denoising, a higher signal-to-noise ratio, and lower mean square error.
1. Introduction
Grinding single crystal diamond is critical. During the process, redundant motion between the tool and grinding disc can affect the tool's quality. Vibration signals are important for monitoring tool quality and wear, helping control vibrations, and improving grinding efficiency and tool lifespan. However, in practice, noise from equipment, tools, and the environment often affects the process [1]. Effectively removing this noise can enhance information quality and ensure signal accuracy.
The wavelet threshold denoising algorithm is a common signal processing method. Traditional threshold functions, such as soft and hard thresholds, were introduced by Donoho and Johnstone [2] in 1995 to denoise signals by processing wavelet coefficients. However, this method can lead to unsmooth signals and constant deviations. Q. Qian [3] et al. proposed an improved threshold function with two factors for fault signal denoising. To address noise in bearing vibration signals, M. Qin [4] suggested using a genetic algorithm to optimize the wavelet threshold function and find the best parameter combination. H. Ma [5] et al. used the hard threshold method for vibration signal denoising and determined the threshold value based on the signal's standard deviation.
To reduce noise and improve the signal-to-noise ratio, this paper introduces an improved wavelet threshold function with adjustable parameters. These parameters enhance adaptability, but their selection impacts denoising. To optimize this, IGA is used to find the best parameters. GA, introduced by John Holland [6], is based on biological evolution but can suffer from quick convergence, local optima, and limited global search. To address this, the fitness function and genetic strategy are refined to improve global search and maintain stable convergence.
2. Wavelet threshold denoising
2.1. The basic principle of wavelet threshold denoising
Wavelet threshold denoising decomposes a signal using the wavelet transform to target high-frequency noise. The wavelet coefficients are next treated using a threshold: hard thresholding puts coefficients below the threshold to zero, and soft thresholding decreases coefficients above the threshold while setting those below to zero. The treated coefficients are reassembled to generate the denoised signal. The flow chart for this procedure is depicted in Fig. 1 [7].
Fig. 1Flow chart of wavelet threshold denoising

2.2. Soft and hard threshold functions
Soft threshold functions and hard threshold functions as shown in Eq. (1) and Eq. (2). and respectively represent the coefficients before and after denoising, and is the predetermined threshold:
The soft threshold function has the advantage of being smoothed and maintaining continuity at the threshold setting. However, there is a fixed discrepancy between the wavelet coefficient processed by the soft threshold function and the actual signal, resulting in distortion of the reconstructed signal.
The hard threshold function can effectively preserve the original signal's edge characteristics, yet it suffers from discontinuity. Specifically, discontinuities arise at threshold values of + and –, leading to oscillations and significant variance in the reconstructed signal, ultimately causing signal deviation [8].
2.3. Improved wavelet threshold function
Eq. (3) demonstrates the proposed improved wavelet threshold function in this study, which integrates the advantages and limitations of the conventional wavelet threshold function:
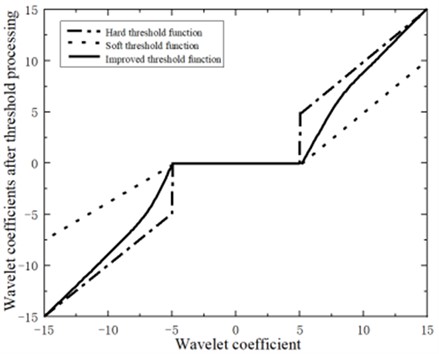
In the Eq. (3), the wavelet coefficient after threshold processing is denoted as , while the wavelet coefficient before threshold processing is denoted as . The set threshold is represented by , and the adjustable parameter is denoted by . The three denoising functions are shown in Fig. 2.
The adjustable parameter α is introduced in the modified wavelet threshold function, which is based on the traditional threshold function. This addition can enhance the function’s flexibility to accommodate a range of signals, and the size of can be suitably adjusted for different signal processing scenarios. The improved wavelet threshold function approaches the hard threshold function more closely the greater , and vice versa. Between the soft and hard threshold functions lies the improved wavelet threshold function. As approaches infinity, also approaches infinity, making approach . This improved wavelet threshold algorithm addresses the consistent deviation and distortion in the reconstructed signal associated with the soft threshold technique. When approaches the threshold , approaches , this improvement tackles the signal discontinuity issue previously linked to the hard threshold function.
Due to the different selection of adjustable parameter , the denoising effect will be very different, so IGA is selected to optimize the adjustable parameter , which forms the denoising effect. To produce the best denoising effect, the wavelet threshold function with the higher SNR is built.
Fig. 2Soft threshold, hard threshold and improved wavelet threshold function
3. IGA optimizes adjustable parameters
By imitating the process of biological evolution in nature, GA continuously optimizes individuals in the space through selection, crossover and mutation operations, so as to find the optimal solution or approximately optimal solution to the problem. The benefits of GA include excellent computing efficiency, high robustness, and high application. Nevertheless, there are several issues with the traditional GA in real-world applications, namely its slow convergence time and susceptibility to local optimal difficulties, which calls for improvements.
3.1. Improvement of fitness function
The fitness function evaluates individuals and affects their selection probability, influencing evolution and optimization. Normalizing the fitness function scales the values, improving selection and population evolution [9]. This paper uses normalization to enhance the fitness function.
Every individual’s fitness value is computed after the fitness function’s initial value range has been established. These values are then mapped to the interval [0, 1] using a linear normalization method, as shown in Eq. (4). Where min and max are the minimum and maximum fitness function values respectively, and is the normalized fitness function value. Finally, the normalized fitness function value is calculated as the new fitness value of each individual in the genetic algorithm:
The improved genetic algorithm ensures that individual fitness values are on a uniform scale, avoiding instability from different fitness ranges, and enhances both convergence speed and optimization results.
3.2. Improvement of genetic strategies
Since the solutions obtained by the genetic algorithm are random, elite and roulette choices are used to avoid sub-optimal solutions. Elite selection keeps the most suitable individuals in the group, while roulette selection individuals based on their fitness ratio.
In each generation, the elite individuals are first retained and copied into the next generation to maintain their genetic traits. Roulette selection is then used to choose the remaining individuals based on their fitness values to form the parent population for crossover and mutation. Crossover creates new offspring from the selected parents, and mutation randomly alters the offspring’s genes with a set probability. Finally, the elite individuals are combined with the new offspring to form the next generation, which will continue to evolve.
Elite selection makes sure the optimal individual is not overlooked and enhances the algorithm’s capacity for worldwide search. Roulette selection preserves population diversity and prevents premature convergence to local optimality. Together, they balance population diversity and convergence rate.
3.3. IGA optimization parameter steps
(1) Initialize the population and determine the optimal interval through chromosome coding.
(2) The fitness function is determined to be the SNR, whose function expression is shown in Eq. (5). Where, is the original signal, is the signal processed by the wavelet threshold function, and is the signal length:
(3) The fitness value is calculated by the fitness function of the normalized treatment. According to the obtained fitness values, individuals are selected with an improved selection strategy.
(4) If the termination condition is satisfied, the optimal parameters can be output, and the improved wavelet threshold function can be determined to denoise the signal.
4. Simulation experiment analysis
To demonstrate the method’s effectiveness, experiments are conducted using MATLAB R2018b on a PC. Vibration signals collected by a ULT20 sensor on a DAP-VI grinding machine are denoised.
Comparisons are made between the soft threshold function, hard threshold function, improved wavelet threshold function, GA-optimized wavelet threshold function, and IGA-optimized wavelet threshold function. At the same time, the denoising index Eq. (5) SNR and Eq. (6) MSE are introduced for comparative verification. Where, is the original signal, is the signal processed by the wavelet threshold function, and n is the signal length:
The original signal is shown in Fig. 3. Five different denoising functions are applied to the collected signal using the db4 wavelet basis function, with 5 decomposition layers and the same threshold [10]. The denoising results for each function are displayed in Fig. 4-6.
Subsequently, the better wavelet threshold function is optimized using the IGA method described in this research. The genetic algorithm parameter is set, the parameter –1, is chosen, the population initialization size is 20, and there are 20 iterations. Fig. 7 and FIG. 8 illustrate the impact of the improved wavelet threshold function that was optimized using GA and IGA.
The denoising findings demonstrate that the signal processed by the improved wavelet threshold function may preserve the smoothness of the signal while retaining its peak characteristics, resulting in a good denoising effect.
Fig. 3Original signal
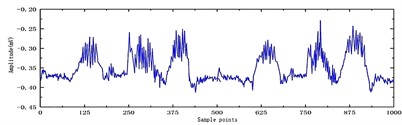
Fig. 4Soft threshold function
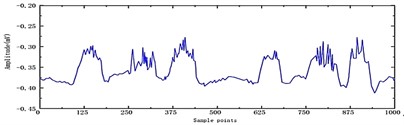
Fig. 5Hard threshold function
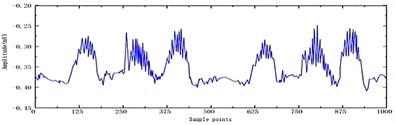
Fig. 6Improved wavelet threshold function
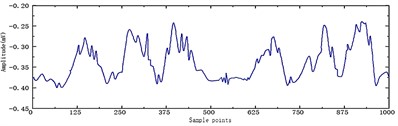
Fig. 7GA-Improves wavelet threshold function
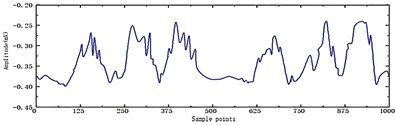
Fig. 8IGA-Improves wavelet threshold function
As indicated in Table 1, the denoising performance is measured using the SNR and MSE. With an SNR that is 3.72 % higher than the soft threshold and 1.67 % higher than the hard threshold, the improved wavelet threshold function performs noticeably better than the conventional wavelet threshold function. Compared to the GA-optimized function, the SNR of the IGA-optimized function is 2.12 % higher. Furthermore, the IGA-optimized wavelet threshold function has 5.93 % lower MSE than the GA-optimized function, and the improved wavelet threshold function has the lowest MSE, 6.45 % lower than the soft threshold and 8.63 % lower than the hard threshold.
Table 1Comparison of denoising indicators of each function
SNR | MSE | |
Soft threshold function | 34.242 dB | 0.713×10-2 |
Hard threshold function | 34.935 dB | 0.730×10-2 |
Improved wavelet threshold function | 35.517 dB | 0.667×10-2 |
GA optimization improves the wavelet threshold function | 35.964 dB | 0.657×10-2 |
IGA optimization improves the wavelet threshold function | 36.726 dB | 0.618×10-2 |
5. Conclusions
For the noisy vibration signals from grinding single crystal diamond tools, an improved wavelet threshold function is proposed, with the adjustable parameter α optimized by IGA for better denoising:
1) Function Improvement: Analyzing the pros and cons of soft and hard threshold functions led to the development of an improved wavelet threshold function. The introduction of parameter α makes the function adaptable for different signals, providing smoother and distortion-free results compared to traditional wavelet threshold functions.
2) IGA Optimization: To enhance denoising, IGA optimizes the parameter , improving the GA’s fitness function and genetic strategy. This addresses issues of slow convergence and weak global search ability found in traditional GA.
3) Verification: To validate the approach, MATLAB R2018b was utilized. As compared to soft and hard threshold functions, the IGA-optimized wavelet threshold function obtains a 3.72 % and 1.67 % higher SNR, respectively, and an MSE reduction of 6.45 % and 8.63 %, according to the results. The IGA-optimized function has a 2.12 % better SNR and a 5.93 % lower MSE than the GA-optimized function, indicating the superiority of the suggested approach.
References
-
H. Ma, S. Wang, and R. Ji, “Grating cutting tool grinding vibration control,” Journal of Changchun University of Technology, Vol. 37, No. 6, pp. 550–554, 2016, https://doi.org/10.15923/j.cnki.cn22-1382/t.2016.6.07
-
S. Du et al., “An improved wavelet threshold denoising algorithm,” Microelectronics and Computers, Vol. 38, No. 2, pp. 40–46, 2021.
-
Q. Qian, B. Dong, and X. Shao, “The application of improved wavelet threshold denoising in bearing fault diagnosis,” Data Communication, No. 4, pp. 17–20, 2020.
-
M. Qin, “Fault diagnosis of rolling bearing based on vibration signal,” Inner Mongolia University of Science and Technology, 2022.
-
H. Ma, D. Xia, and Y. Wu, “Online orientation recognition of single-crystal diamond tools in the process of indexing grinding based on HMM and multi-information fusion,” Applied Sciences, Vol. 14, No. 10, p. 4236, May 2024, https://doi.org/10.3390/app14104236
-
H. Wang, X. Zhao, and X. Yuan, “Robot path planning based on improved adaptive genetic algorithm,” Electric Light and Control, Vol. 29, No. 5, pp. 72–76, 2022.
-
W. Li, W. Xu, and T. Zhang, “Improvement of threshold denoising algorithm based on wavelet transform,” Computer Simulation, Vol. 38, No. 6, pp. 348–351, 2021.
-
L. Chen, “Based on the improved wavelet threshold algorithm of signal denoising,” Journal of Laser, Vol. 36, No. 3, pp. 92–95, 2015, https://doi.org/10.14016/j.cnki.jgzz.2015.03.092
-
W. Weng et al., “Obstacle avoidance path planning of mobile robot based on improved genetic algorithm,” Journal of Ningde Normal University (Natural Science Edition), Vol. 36, No. 2, pp. 133–142, 2024, https://doi.org/10.15911/j.cnki.35-1311/n.2024.02.005
-
H. Ma, Y. Chen, and F. Cai, “Application of improved wavelet threshold denoising method in Motor current Signal Processing,” Mechanical and Electrical Engineering Technology, Vol. 51, No. 11, pp. 55–57, 2022.
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
