Mathematical modeling of piezoceramic spherical shell actuator for vibration generating devices

1. Introduction

This article addresses the relevance of piezoceramic spherical shell actuators, which provide a high level of accuracy and stability in the process of generating vibrational oscillations across a wide range of amplitude-frequency characteristics. The spherical shape of these actuators is chosen because it allows for the uniform distribution of mechanical stresses across the actuator’s surface, thereby enhancing its durability and efficiency compared to traditional flat or cylindrical designs. The study presents analytically derived mathematical models and formulas for determining the electrical impedance of piezoelectric elements and analyzes the dependence of impedance amplitude on frequency and the charge ratio on the polarized surfaces of the spherical piezoceramic element. The proposed model allows for the determination of electrical impedance as a function of cyclic frequency and various parameters (geometric, physical and mechanical, electrical) of the actuators.

The modern development of technologies related to vibration-generating devices primarily depends on the use of advanced materials and designs that ensure increased efficiency and reliability under various operating conditions. One such promising direction is the use of piezoceramic actuators, particularly those based on a spherical shell construction [1]. Mathematical modeling of such actuators is a key aspect of developing effective vibration-generating systems that have a wide range of applications in promising fields of healthcare and industry, such as medicine, pharmaceuticals, microelectronics, aerospace, and more.

The relevance of the research conducted in this article lies in the fact that piezoceramic spherical shell actuators provide a high level of accuracy and stability in the process of generating vibrational oscillations over a wide range of amplitude-frequency characteristics, which is critically important for most modern devices that require precise control of vibration parameters [2]. For example, the spherical shape of the shell allows for the even distribution of mechanical stresses across the entire surface of the actuator, which increases its durability and efficiency compared to traditional flat or cylindrical designs [3].

In the work [4], author Moon Kyu Kwak conducts dynamic modeling and develops control algorithms for digital controllers, including measurement methodologies and actuators. The article [5] analyzes the vibration response of a structure to external harmonic excitation, allowing for the study of control parameters to reduce tremor. Meanwhile, in [6], axisymmetric transverse bending vibrations of a bimorph piezoelement are investigated. However, as noted in works [7-10], there is currently no systematization of methods for the calculation and modeling of piezoceramic actuators, complicating the development of a generalized mathematical model. Specifically, for spherical shell actuators, where radially distributed vibrations are typically used, there is an urgent need to develop the theory of harmonic radial vibrations of piezoceramic cylindrical shells with limited height. Therefore, the development and experimental validation of mathematical models of piezoelectric spherical actuators for vibration-generating devices are currently relevant.

The aim of this article is to develop a mathematical model of a piezoceramic spherical shell actuator, which will allow for more accurate calculation of its electrical impedance, thus predicting its behavior under various load conditions and ensuring increased efficiency of vibration-generating devices.

This scientific article contributes to the development of modern vibration technologies and may help improve the efficiency and reliability of vibration-generating systems in various fields of their application.

2. A mathematical model of a piezoceramic spherical shell

We calculate the electrical impedance $Z_{el}\left(\omega \right)$ of an oscillating open spherical piezoceramic shell (Fig. 1). Let us assume that the surfaces $\rho =R$ and $\rho =R+\alpha$ of the shell have electrode-coated using the combined technology thoroughly discussed in [11, 12]. The shell’s material is polarized along the thickness, i.e., along the direction of the radial axis or in the spherical coordinate system $\left(r,\phi ,\vartheta \right)$. In this case, obviously, the material constants of piezoceramics are determined by matrices [13].

Here we consider the frequency range in which the wavelength of elastic vibrations significantly exceeds the $\alpha$ thickness of the shell. If the shell vibrates in a vacuum, then the following statements are true:

In the case of an axisymmetric, i.e., independent of the values of the azimuthal angle $\phi$, stress-strain state of a spherical shell, in the general case, the following set of elastic stresses can exist in its volume and on its surface:

Fig. 1An open spherical piezoceramic shell

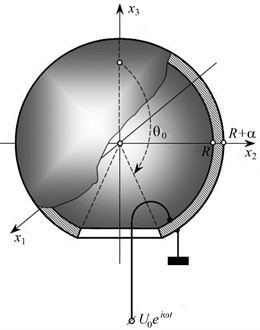
Condition ${\sigma }_{rr}=0\forall r\in \left[R,R+\alpha \right]$ implies that:

Consequently:

where $c_{22}=c_{22}^E-{\left(c_{12}^E\right)}^2/c_{11}^E$; $c_{12}=c_{12}^E\left(1-c_{12}^E/c_{11}^E\right)$; $e_{12}^{*}=e_{12}-e_{11}{c}_{12}^E/c_{11}^E$ are material constants of piezoceramics for the mode of harmonic oscillations at constant (zero) normal voltage ${\sigma }_{rr}$.

The electrical axisymmetric state of a spherical shell is to be determined, in the general case, by the radial and polar components $D_r$ and $D_{\vartheta }$ of dielectric flux density vector. These components are defined as:

where ${\chi }_{11}^{\sigma }={\chi }_{11}^{\epsilon }+e_{11}^2/c_{11}^E$ is the dielectric piezoceramic constant in the mode of harmonic oscillations at constant (zero) normal stresses ${\sigma }_{rr}$.

Similarly to the case of a cylindrical shell [14], based on the condition ${\sigma }_{r\vartheta }=0$$\forall r\left[R,R+\alpha \right]$ we demonstrate that ${\epsilon }_{r\vartheta }=$ 0 and $E_{\vartheta }=$ 0, which is equivalent to $D_{\vartheta }=0$$\forall r\in \left[R,R+\alpha \right]$.

Thus, the polarization effects (electrical state) in a strained spherical piezoceramic shell are determined by the radial component $D_r$ of the dielectric flux density vector. Condition $div\overrightarrow{D}=0$ implies that $\frac{1}{r^2}\left[\frac{\partial }{\partial r}\left(r^2{D}_r\right)\right]=0$ from whence we find $D_r=C_1/r^2$, where $C_1$ is the constant to be defined.

Remembering that $E_r=-\partial \mathrm{\Phi }\left(r\right)/\partial r$, where $\mathrm{\Phi }\left(r\right)$ is the scalar potential of the electric field in the volume of strained piezoceramics, we obtain the equation:

Integrating the left and the right sides of Eq. (10), we obtain the expression:

where $C_2$ is the integration constant.

Since $\mathrm{\Phi }\left(R\right)=U_0$, and $\mathrm{\Phi }\left(R+\alpha \right)=$0 (Fig. 1), the constant $C_2=$ 0, while the $C_1$ constant is to be determined by the following expression:

Thus, the radial component $D_r$ of the dielectric flux density vector necessary to determine the electrical impedance $Z_{el}\left(\omega \right)$ of a spherical piezoceramic shell will be calculated by the formula:

The electric charge $Q$ on the surface $r=R$ defines as the integral over area. Since the area element is $dS=R^2\mathrm{s}\mathrm{i}\mathrm{n}\vartheta d\vartheta d\phi$, the following implies:

In the integrand Eq. (14) we consider a new variable $\xi =\mathrm{c}\mathrm{o}\mathrm{s}\vartheta$. Then $\mathrm{s}\mathrm{i}\mathrm{n}\vartheta d\vartheta =–d\xi$ and:

For an axisymmetric stress-strain state of the open spherical shell, the strain tensor components ${\epsilon }_{\phi \phi }$ and ${\epsilon }_{\vartheta \vartheta }$ are found by the following relations:

where $u_r\left(\vartheta \right)$ and $u_{\vartheta }\left(\vartheta \right)$ are radial and polar components of the material particle displacement vector of an oscillating spherical shell.

Based on the found sensitivity of the piezoceramic shell in the inverse piezoelectric effect mode, i.e., assuming that $u_r\left(\vartheta \right)=U_0{f}_r\left(\vartheta \right)$ and $u_{\vartheta }\left(\vartheta \right)=U_0{f}_{\vartheta }\left(\vartheta \right)$, the equation reads as:

Condition ${\epsilon }_{r\vartheta }=0\forall r\in \left[R,R+\alpha \right]$ implies that if $\partial /\partial r=0$, this condition is equivalent to the statement $\frac{\partial u_r\left(\vartheta \right)}{\partial \vartheta }-u_{\vartheta }\left(\vartheta \right)=0\forall r\in \left[R,R+\alpha \right]$, from whence it follows that $f_{\vartheta }\left(\vartheta \right)=\frac{\partial f_r\left(\vartheta \right)}{\partial \vartheta }$.

Using relation last equation to exclude the $f_{\vartheta }\left(\vartheta \right)$ function from the square bracket in formula Eq. (16), we obtain the notation:

Further, we introduce the notation $C_{ss}^{\sigma }=2\pi R\left(1+\alpha /R\right)\left(1-\mathrm{c}\mathrm{o}\mathrm{s}{\vartheta }_0\right){\chi }_{11}^{\sigma }/\alpha$ and this quantity will be termed the dynamic electric capacitance of an open spherical piezoceramic shell. Counting this notation and definition Eq. (17) of the total strain, the expression Eq. (15) takes the following form:

where $F_{ss}\left(\mathrm{\Gamma },\mathrm{\Pi }\right)$ is a dimensionless frequency-dependent function determined by a set of geometric (symbol $\mathrm{\Gamma }$) and physical-mechanical ($\mathrm{\Pi }$) parameters of a spherical open piezoceramic shell. The numeric values of the $F_{ss}\left(\mathrm{\Gamma },\mathrm{\Pi }\right)$ function are found by the following expression:

Since the amplitude value of the current is $I=-i\omega Q$, the electrical impedance of an open spherical shell is found (at this stage it is obvious) by the standard expression:

Ultimately, Eq. (19) is valid for the high-frequency vibration range, where both radial and axial displacements of the material particles of the sphere occur simultaneously, meaning that the wavelength of the elastic wave becomes comparable to the thickness of the spherical actuator.

Let’s examine the results of the mathematical modeling of the piezoceramic spherical shell actuator and analyze its electrical impedance in the high-frequency range.

At $e_{12}^{*}=$ 0, function $F_{ss}\left(\mathrm{\Gamma },\mathrm{\Pi }\right)=$ 0, and expression Eq. (19) simplifies to the formula for calculating the reactance of a capacitor with electrical capacitance $C_{ss}^{\sigma }$.

It is important to note that the electrical impedance of the sphere is determined by the averaged values of the displacement vector components of the material particles, which leads to their transformation into ordinary differential equations that can be solved with a certain degree of accuracy. However, such a system of partial differential equations cannot be solved in its general form.

As for the medium and low-frequency ranges, the application of spherical shell piezoelectric actuators at these frequencies is impractical. Due to the peculiarities of the electroelastic state of the vibrating spherical transducer, at low frequencies, there is a negative change in the numerical values of the dynamic electrical capacitance and the analytical structure, thereby reducing the efficiency of such devices.

3. Discussion of simulation results

The above examples of the general definition for the electrical impedance of oscillating piezoceramic elements are sufficient to conclude that the fundamental condition $div\overrightarrow{D}=0$ completely determines the electrical state of the objects under study. Moreover, fulfillment of $div\overrightarrow{D}=0$ condition produces the definitions of the electric field strengths that appear in the generalized Hooke’s law formulations, i.e., the $div\overrightarrow{D}=0$ condition indirectly determines the elastic stresses that arise in the volume and on the surface of oscillating piezoceramic elements. In other words, fulfillment of the fundamental condition $div\overrightarrow{D}=0$ should precede any calculation of characteristics and parameters of oscillating piezoceramic elements [15]. This, perhaps, is one of the principles of mathematical modeling of the characteristics and parameters of oscillating piezoceramic elements [16].

Fig. 2 demonstrates the frequency-dependent variation of the dimensionless function $F_{co}\left(\omega \right)$, which was calculated for a set of geometric, physical, and mechanical parameters: $c_{11}^E=$ 110 GPa; $c_{12}^E=$ 60 GPa; $c_{33}^E=$ 100 GPa; $e_{33}=$ 18 C/m²; $e_{31}=$ – 8 C/m²; ${\chi }_{33}^{\epsilon }=$ 1400${\chi }_0$ (its parameters are characteristic of PZT-piezoceramics).

Fig. 2Frequency-dependent alteration in the modulus of function Fcoω

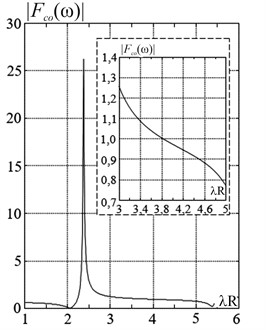
The inset in Fig. 2 shows the variation of the function’s modulus in the range of dimensionless wave numbers close to the resonant values. The calculated value of this function enables the determination of the modulus of dynamic electrical capacitance in the spatial vibration mode of a piezoceramic spherical shell, and consequently, the assessment of the actuator's efficiency compared to actuators of other shapes. Spherical shell piezo actuators exhibit several positive effects compared to cylindrical and disk actuators [13-16], in particular:

1) Higher quality factor: due to their geometry, spherical shells can achieve a quality factor in the range of 500-800, significantly exceeding the values for cylindrical (300-500) and disk actuators (200-400).

2) Reduced electrical impedance: the spherical shape of the actuator helps lower electrical impedance to 10-20 Ohms, which is considerably lower than that of cylindrical (20-50 Ohms) and disk actuators (30-70 Ohms).

3) Wide range of resonant frequencies: spherical shell actuators can operate within a resonant frequency range from 1 kHz to 1 MHz, maintaining stable characteristics across different frequencies, while cylindrical and disk actuators typically operate between 10 kHz and 500 kHz.

4) Stability in operation: thanks to their spherical geometry, these actuators have 20-30 % better resistance to deformation, reducing the likelihood of unwanted oscillations.

5) Lower susceptibility to local resonances: spherical actuators are 15-25 % less prone to local resonances compared to disk and cylindrical actuators, which positively impacts the quality and precision of vibration generation.

4. Conclusions

In the course of the research, mathematical models were analyzed, and the derived formulas for determining the electrical impedance of piezoelectric elements were compared. Additionally, the dependence of the amplitude of electric current in the conductors of the circuit used for measuring the electrical impedance of a spherical piezoceramic element on frequency and the signs of the charge ratio on its polarized surfaces was studied.

The proposed problem of constructing a mathematical model of piezoelectric spherical shell actuators results in the determination of the dependence of electrical impedance on cyclic frequency and a set of parameters (geometric, physics and mechanical, electrical) for such actuators.

The obtained analytical dependencies, which can determine the electrical impedance and the amplitude values of current and electric charge on the electrode surface of the piezoelectric spherical shell actuator under the conditions of the reverse piezoelectric effect, allow for the complete solution of the problem of harmonic axisymmetric oscillations of a piezoelectric spherical shell of a specific diameter.

A frequency-dependent change in the quality factor and electrical impedance of the spherical shell model of the PZT-19 piezoceramic actuator was established, which oscillates. This revealed a higher quality factor (2-2.5 times higher compared to disk actuators and 1.4-1.8 times higher compared to cylindrical actuators) and a sharp decrease in such impedance (2.5-7 times) compared to cylindrical and disk actuators, occurring at electromechanical resonance frequencies around 2.4 kHz.

The evaluation of the efficiency of the spherical actuator compared to actuators of other shapes showed that these spherical actuators have 20-30 % better resistance to deformation compared to others, reducing the likelihood of unwanted oscillations and improving operational stability. Additionally, spherical actuators exhibit a 15-25 % lower tendency towards local resonances compared to disk and cylindrical actuators, which positively impacts the quality and accuracy of vibration generation.

The work presents data obtained as a result of the experimental scientific and technical development “Development of an automated ultrasonic system for extracting plant raw materials in the production of multi-nutrient functional beverages for the rehabilitation and prevention of post-traumatic stress disorders” (state registration number: 0124U000713, 2024-2025), conducted at the Cherkasy State Technological University.