Detecting coherence between oscillators in heavy-noise environments with a moving block bootstrap

1. Introduction

Identifying the couplings between processes is an important task in many areas of science and engineering. These interdependences have been quantified in various ways. Among the most robust and therefore the most frequently applied techniques are synchronization measures and cross-spectral analysis. This resulted from the fact that both approaches are robust with respect to noise, one of the key requirements in most applications. The cross-spectral analysis approach additionally provides information on the frequency at which an interaction is strongest, a feature that is strongly desirable in applications to noisy nonlinear oscillatory systems [1]. Moreover, it is argued [2, 3], that for noisy data in some cases the results for Fourier coherence are (slightly) more robust than for phase synchrony; if the signal is weak it is more likely that noise will destroy the phase structure. Detecting relationships between experimental data becomes a challenge when the data are very noisy. When the signals are nonlinear, and especially chaotic, applying the noise reduction techniques, including chaos-based approaches for such a purpose, can lead to erroneous estimation of the actual degree of interdependence between oscillators with narrowing bandwidth [4, 5]. For high noise levels significant coherence detection can be formulated as hypothesis testing. Moving block bootstrap (MBB) method [6-10] was introduced as an adaption of the ordinary bootstrap for serially correlated data and significantly improves statistical inference for noisy data. The general idea of MBB is to provide the distribution of a statistics based on the measured signals alone, when the analytic derivation of the statistics is not known. Once this empirical distribution is obtained from the bootstrap, confidence intervals can be derived and hypothesis tests can be performed based on the empirical quantiles. Based on this technique, the significance of the coupling between two time series is commonly assessed by setting a threshold level in the coherence function [6-8]. When noise is strong, however, the accuracy of the MBB approach to calculate confidence intervals from the asymptotic distribution function of the sample coherence function is degraded. On the other hand, it has been shown that some approaches based on surrogate data and the corresponding null hypothesis that the oscillators are unsynchronized or expected coherence is equal to zero at all frequencies can lead to false conclusions, because surrogate techniques like phase randomization suffer from the problem that not only is the interaction between the systems neutralized but the systems themselves are also linearized [11, 12]. This problem calls for a threshold level to be set in the estimated genuine coherence in order to assess whether the two series are significantly coupled or not.

The aim of this paper is to propose a simple coherence detection algorithm in heavy-noise environments based on the two-way MBB technique with a novel defined significance threshold. The performances of the proposed method are illustrated by simulations of the phase synchronization effects between two coupled chaotic Rössler oscillators.

2. Coherence and moving block bootstrap MBB

The coherence between two processes is a measure of the linear relationship of the two at a specific frequency. For two real stationary zero-mean processes $X\left(t\right)$ and $Y\left(t\right)$, the cross spectrum $S_{XY}\left(\omega \right)$ is defined as the Fourier transform of the cross-covariance function $F_{XY}\left(\tau \right)=〈X\left(t\right)Y\left(t-\tau \right)〉$ [13]. The coherence function, also called the magnitude squared coherence function, ${\left|C_{XY}\left(\omega \right)\right|}^2$ at frequency $\omega$ is given by the modulus of the cross-spectrum $S_{XY}\left(\omega \right)$ normalized by the respective auto-spectra $S_X\left(\omega \right)$ and $S_Y\left(\omega \right)$ [13]:

For simplicity we shall refer to ${\left|C_{XY}\left(\omega \right)\right|}^2$ as the coherence. It measures the extent to which $Y\left(t\right)$ is determinable from $X\left(t\right)$ at frequency $\omega$ by linear time-invariant operations and is bounded between zero and one. An estimate of the coherence ${\left|{\widehat{C}}_{XY}\left(\omega \right)\right|}^2$ is obtained by replacing the cross- and auto-spectra in Eq. (1) with their respective estimated quantities obtained by averaging or smoothing cross- and auto-periodograms.

Briefly, MBB is a nonparametric bootstrap method that can be applied to dependent observations [6-9]. The concept of MBB consists of calculating the estimator of interest over replicated pseudo-data obtained by random drawing with replacement from the blocks of consecutive data [8]. In more detail, from the $n$ available samples of the time series $X\left(t\right)$ random selection of blocks of length $b$ from the original data takes place. Then these blocks are concatenated together to obtain a replicated bootstrap pseudo-data. As a result of the MBB procedure, approximations of unknown distributions of root statistics are obtained. These approximations allow the construction of confidence intervals, and then building tests for different problems. Typically, hundreds and thousands of resamples are recommended for reliable testing.

3. Description of the algorithm

To obtain a mean coherence measure with MBB, we proceed as follows. Let $\mathcal{X}=\left\{X\left(1\right),Y\left(1\right),\dots ,X\left(n\right),Y\left(n\right)\right\}$ be a bivariate time series of length $n$. Let the integer $b$ be the block length, define $B_{t,b}=\left\{X_t,Y_t,\dots ,X_{t+b-1},Y_{t+b-1}\right\}$, and $k=⌊n/b⌋$ is assumed to be an integer. Using random number generator to generate $k$ integer values $i_1$,…, $i_k$ from the uniform distribution on the set $\left\{\text{1, 2, …,}n-b+\text{1}\right\}$ and joining the $k$ blocks each of length $b$, such as $B_{i1,b}$, …, $B_{ik,b}$, we draw the MBB sample ${\mathcal{X}}^{*}=\left\{{X\left(1\right)}^{*},{Y\left(1\right)}^{*},\dots ,{X\left(n\right)}^{*},{Y\left(n\right)}^{*}\right\}$ of the same size $n$. The MBB version of the coherence estimator ${\left|{\widehat{C}}_{XY}^{*}\left(\omega \right)\right|}^2$ is calculated by replacing in Eq. (1) the estimates ${\widehat{S}}_X\left(\omega \right)$, ${\widehat{S}}_Y\left(\omega \right)$, and ${\widehat{S}}_{XY}\left(\omega \right)$ with their bootstrap counterparts, i. e.:

Repeating the MBB procedure $B$ times we obtain a total of $N$ bootstrap statistics ${\left|{\widehat{C}}_{XY}^{*1}\left(\omega \right)\right|}^2$,…, ${\left|{\widehat{C}}_{XY}^{*N}\left(\omega \right)\right|}^2$ and a mean coherence measure is calculated:

The mean coherence measure radically reduces spurious maxima that may lead to misleading interpretations. However, for high noisy time series, the variance at some frequencies outside the dominant frequency range:

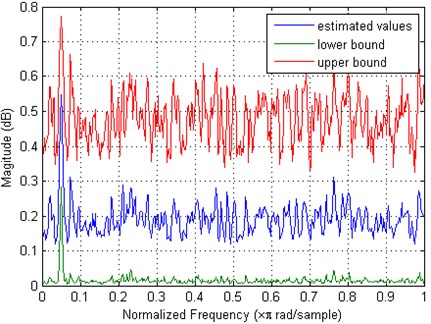
remains high, and non-zero mean coherence values are likely to occur at some frequencies outside the dominant frequency range, as illustrated in Fig. 1.

Moreover, the upper bound of the 95 % confidence interval of spurious peaks can exceed the estimated mean coherence at dominant frequency. This problem calls for appropriate threshold level to be set in the estimated coherence so we can assess whether the two series are significantly coupled or not. We propose a novel but simple method for defining the threshold, which is based on two MBB procedures: a) bootstrap resampling in the context of bivariate time series model and b) bootstrap resampling for each variable separately. Namely, the threshold is defined as the upper bound of a 95 % confidence interval for bootstrapping coherence performed with independent bootstrap indexes for time series $X\left(t\right)$ and $Y\left(t\right)$, which results in destroying of the dependence between the time series under consideration. The bootstrap using independent bootstrap indexes for time series $X\left(t\right)$ and $Y\left(t\right)$ can be treated as a two-dimensional surrogate method in respect of coherence. As a result, the structural properties of the original time series are maintained but the bootstrapped series are structurally uncoupled. Because no dominant coherence between randomly resampled time series $X\left(t\right)$ and $Y\left(t\right)$ should occur, it is reasonable to define the constant threshold as the new upper bound of a 95 % confidence interval over all frequencies of the spectrum. The null hypothesis that the two series are not coherent against the alternative that the two series are significantly coupled, i. e., the observed mean coherence measure derived from the bootstrap statistics is greater than the defined threshold, is examined by performing $t$-tests at each frequency of the spectrum.

Fig. 1The mean coherence measure with 95 % confidence bounds between two coupled Rössler oscillators derived after 480 bootstrap realizations at SNR = –15 dB

4. Simulation results

We consider the following system of two coupled chaotic Rössler oscillators [14, 15]:

where ${\omega }_1=$0.98 and ${\omega }_2=$1.02. With coupling strength $c=$0.035, the coherent systems are synchronized. The spectral peak of the measured data is located around the normalized frequency 0.05 ($\times \pi$ rad/sample). We generate a time series using the ODE45 integrator of Matlab. The solution was sampled at time intervals $t=$ 0.1 and 2500 samples, after the first 200 samples have been discarded, are adopted for analysis. The magnitude squared coherence of the input signals $X\left(t\right)$ and $Y\left(t\right)$ were estimated by Welch’s averaged, modified periodogram method and periodic Hamming windows of length to obtain eight equal sections $X\left(t\right)$ and $Y\left(t\right)$ with a 50 % overlap were used. All data processing and analyses were performed with Matlab software (The MathWorks, Natick, MA).

For moving block-bootstrapping, the appropriate choice of the block length $b$ is a key parameter, and the choice of $b$ for a small sample size is not straightforward. For the bootstrap to be effective, $b$ should be large enough for as much of the dependence structure as possible to be retained in the blocks, but not so large that the number of blocks becomes small, resulting in poor estimation of underlying distribution [6]. The method based on the decay rate of the autocorrelation function [16] and a similar approach with respect to discontinuity of the autocorrelation function at time lag zero for noisy time series [7] were proposed for selection of the optimal block length. At strength noise, however, the decay rate of the autocorrelation function cannot be reliably estimated. Therefore, block length, estimated from the decay rate of the autocorrelation function (by fitting an exponential function to the envelope of the empirical autocorrelation function and excluding the zero time lag) was approximated to the floor integer of periods (six) of the autocorrelation function. A similar solution is used in seasonal block bootstrap, which was designed for time series with periodic structure and in which the block length is an integer multiple of the period length [17].

Fig. 2The mean coherence values (black) between two coupled Rössler oscillators and threshold values (red) derived from 100 independent Monte Carlo trials at SNR= – 15 dB

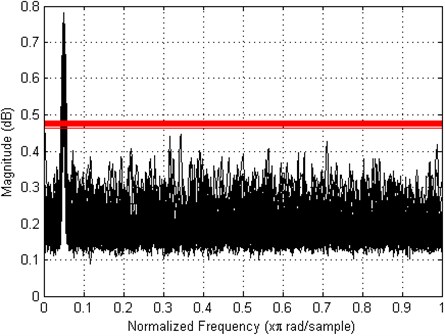
The performance of the algorithm was evaluated by means of a 100-trial Monte Carlo simulation whereby the signals were contaminated by various realizations of additive zero mean white Gaussian noise at a defined signal-to-noise ratio (SNR). Furthermore, these simulations were performed for two versions of random selection of blocks: (i) the blocks of length $b$ started at the time indexes $i_1$,…, $i_k$, where $i_1$,…, $i_k$, are iid from a discrete uniform distribution $\left\{\text{1, 2, …,}n-b+\text{1}\right\}$ as shown above, and (ii) the blocks were selected randomly but with respect to the pseudo periodicity of the processes under consideration, i.e., the blocks started at the time indexes, the distance between which is an integer multiple of the approximated period length. Number of bootstrap realizations $B=$480 was chosen at every trial. Fig. 2 shows the mean coherence values from 100 independent Monte Carlo trials as well as defined threshold values at SNR = –15 dB. As can be seen, the algorithm reliably detects the coherence peak at the oscillation frequency in the vast majority of trials and a small number of false positive errors can occur at some frequencies. The false positive and false negative error rates across trials at different SNR are shown in Table 1.

5. Conclusions

All simulations results performed on coupled chaotic Rössler oscillators, verify the applicable of the proposed algorithm for detecting coherence at the oscillation frequency between oscillators in a strong white Gaussian noise environment. In accordance with this approach, the null hypothesis of absence significant coherence (i.e., at all frequencies) is rejected if the average coherence of MBB resampled data exceeds the $\text{100}\left(\text{1}–\alpha \right)\text{\%}$ quantile for bootstrapping coherence obtained from the surrogate time series, i. e., derived from the MBB procedure using independent resampling indexes for the time series $X\left(t\right)$ and $Y\left(t\right)$. Differently from other surrogate techniques like phase randomization, when not only is the interaction between the systems neutralized but the systems themselves are also linearized [12], the MBB procedure using independent resampling indexes for both time series preserves the structural properties of the original time series. The simulations show that the sensitivity of the algorithm increases (without loss of the specificity) if the distance between blocks is defined in terms of the oscillation period. It is worth noting that for practical applications, significant coherence between oscillators under strong white Gaussian noise background can be detected subjectively on the basis of the fairly pronounced spike at the oscillation frequency of the lower 5 % confidence interval of bootstrapped coherence.