Abstract
A solution for dynamic stress concentration of buried pipeline with different material properties subjected to incident P waves is given by wave function expansion method. Through the quantitative analysis of the dynamic response of pipeline structures subjected to blasting seismic waves, the influence of the incident wave numbers, diameter-thick ratio and buried depth on dynamic stress concentration of both Q235 and X70 pipelines was revealed in the paper.
1. Introduction
Buried pipelines are widely used for the transportation of oil and gas. When suffering impact, they may cause severe secondary disasters [1, 2]. For this reason, numerous researchers use various methods to investigate the problem. The problem has previously been investigated by [3-5]. Sancar and Pao [6] use the wave function expansion method to study the scattering of the plane harmonic pressure wave by two cylindrical cavities in an elastic solid. C. A. Davis [7] used Fourier-Bessel series and a convex approximation to study the transverse response of underground cavities and pipes to incident SV waves. Kattis et al. [8] used the boundary element method to solve the problem of incident P and SV waves by tunnels in an infinite poroelastic saturated soil. The problem was studied by many other researchers [9-11].
The present paper investigated the dynamic response of buried steel pipeline with different material types subjected to blast wave. The material types are Q235 and X70. Utilizing the wave function expansion method, the solutions of Helmholtz Equations are obtained. By utilizing the boundary and continuity conditions between the surrounding soil and the steel pipeline, the results can finally be acquired. The influence factors of the analytical solutions were also presented in the paper.
2. Theoretical analysis model
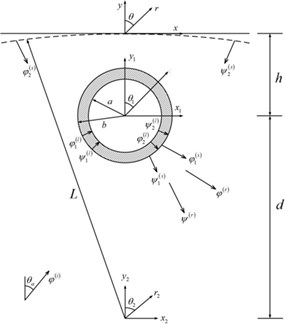
The dynamic response of shallow buried pipeline system impacted by blast wave can be reduced to the diffraction of steady P wave around a circular tube in half infinite space (Fig. 1). The surrounding medium and the pipeline can be assumed as isotropic uniform elastic material. The material properties can be determined by the Lame constants and and density . The inner and outer radius of the pipeline were and respectively, and the buried depth . In order to acquire the wave function that exactly satisfied zero stress condition, we used a convex surface with the radius of curvature to approximate the flat free surface. Previous researches indicated that we could get more exact solution with larger radius . So we choose 104 in the analysis.
3. Wave field in half infinite space
3.1. Incident wave potential function
The incident plane P wave with the frequency has an angle pendicular to the axis of the pipeline. In the rectangular coordinates system, the potential function can be expressed as:
where denotes the incident wave number, ; denotes the P wave velocity in half infinite space; the time factor is ignored.
Fig. 1Analysis model and the coordinate system
3.2. Reflected wave potential function
The incident plane P wave is reflected from the free surface, generating both P wave and SV wave . The incident and reflected waves in the polar coordinate systems are written in the form of Fourier-Bessel series:
where:
and denotes the first kind of Hankel function; denotes Neumann factor: when 0, ; when 0, .
3.3. Scattering wave potential function
In the infinite half space, the incident P wave generates both scattering P wave and SV wave at the interface and the convex surface. There are four scattering waves in the pipeline: two outward propagating waves and two inward propagating waves excited by the incident plane wave. Their potential function can be expressed as:
where , denotes the wave number of P wave and SV wave respectively.
3.4. Solution of the model
At the convex free surface , the continuity conditions are:
At the outer surface of the pipeline , the stress and displacement continuity conditions are:
At the inner surface of the pipeline , the continuity conditions are:
For the plane strain problem of a poroelastic medium, the displacements and the stresses have the following expressions:
where ; and denote the radial and circumferential displacement in the polar coordinate system; , , denote radial stress, the hoop stress and shear stress respectively; , denote Lame constant. Through the above equations we can acquire the stress and displacement of the buried pipeline.
4. Results and discussion
Two different material types are discussed here: Q235 and X70. The influence factors of the dynamic stress concentration factor was studied respectively. The influence factors are defined as follows: denotes the product of the incident wave number and the outer radius of the pipeline, ; denotes the ratio of the outer and inner radius of the pipeline, ; denotes the ratio of buried depth and the inner radius of the pipeline; denotes the incident angle of the blast wave. The value range of the factors can be seen in Table 1.
Table 1The value range of the influence factors
Dimensionless parameters | ||||
Q235 | 1.0 | 1.05 | 2.0 | 30 |
X70 | 0-3.0 | 1.02-1.10 | 1.0-5.0 | 0-90 |
4.1. Influence of incident wave number
Figs. 2(a) and 2(b) show the distribution of on the inner surface of the pipeline for 1.05, 2.0, 30°. The figures indicate that the hoop stress of both Q235 and X70 pipelines are more sensitive to higher space frequency . And Q235 are more sensitive compared with X70.
Fig. 2Distribution of Kθθ on the inner surface of the pipeline
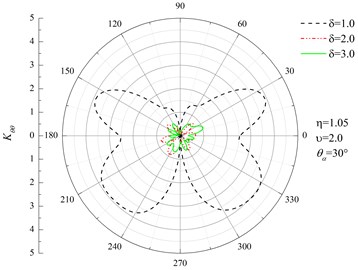
a) Q235
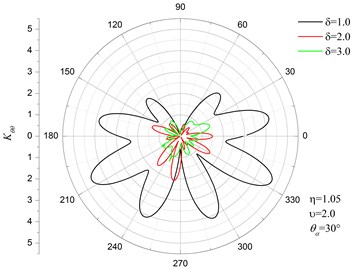
b) X70
Fig. 3Relationship between Kθθ and the incident P wave number
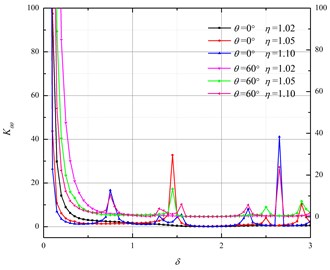
a) Q235
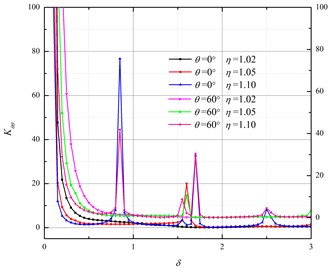
b) X70
Fig. 3 shows the relationships between and the incident P wave number. From Fig. 3(a) and 3(b) we can see decrease exponentially on the intervals with the increase of the incident wave number. This means that the hoop stress of shallow buried pipeline is more sensitive to low frequency blast seismic waves. The value of keeps oscillating on the intervals , with some peak values. For 0º, the peak value increase with the increase of , and reaches to the maximum value when 2.65. For 60º, the peak value decrease with the increase of , and the peak value reaches to the maximum value when 0.85.
4.2. Influence of the diameter-thick ratio
Figs. 4(a) and 4(b) show the relationship between and diameter-thick ratio. In a certain thickness range, the hoop stress of Q235 has three different peak values. The first two values are small and the last one is large. For 5º, the hoop stress reaches to the maximum when the diameter-thick ratio is 1.075. The hoop stress of X70 also has three peak values. But the values are not so quite different compare with Q235. For 60º, the peak value of the hoop stress reaches to the maximum when the incident angle is 15º.
Fig. 4Relationship between Kθθ and diameter-thick ratio
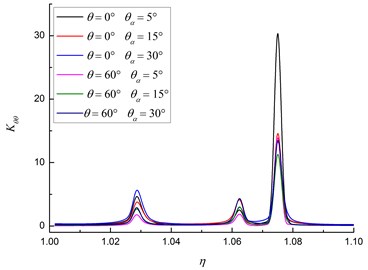
a) Q235
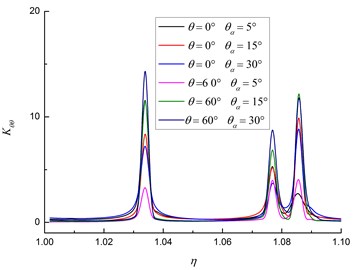
b) X70
4.3. Influence of the buried depth
Figs. 5(a) and 5(b) show relationship between and buried depth of Q235. From the figures we can see that presented a periodic change with the increase of the buried depth. For 1.05, the periodic number reaches to maximum when 0º, 2.0. For 2.0, the periodic number reaches to maximum when 60º, 1.05.
Fig. 5Relationship between Kθθ and buried depth of Q235
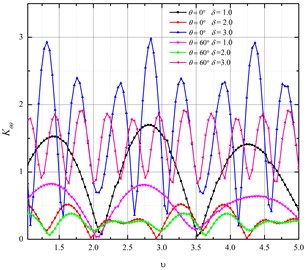
a) 1.05
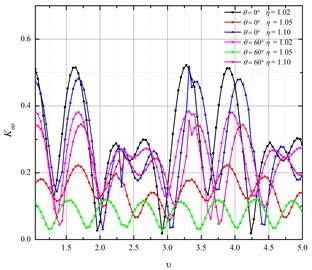
b) 2.0
Figs. 6(a) and 6(b) show relationship between and buried depth of X70. From the figures we can see that also presented a periodic change with the increasing of the buried depth. For 1.05, 60º, the periodic number reaches to maximum when 60º, 3.0. For 2.0, the periodic number reaches to maximum when 1.02, 0º.
Fig. 6Relationship between Kθθ and buried depth of X70
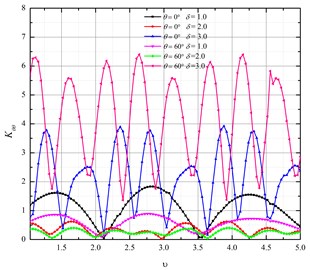
a) 1.05
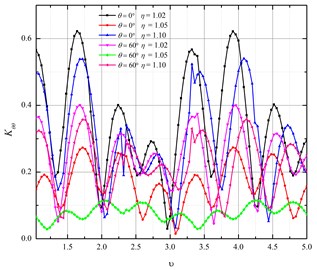
b) 2.0
5. Conclusions
The paper uses the wave function expansion method to study the influence factors of shallow buried pipeline. Numerical results show that, incident wave numbers, diameter-thick ratio and buried depth have direct influence on the response of the pipeline. decrease exponentially on the intervals with the increase of the incident wave number. In a certain thickness range, both of the two pipelines have three peak values, but the forms of the curves are different with each other. also presented a periodic change with the increase of the buried depth. The results can be used in seismic design.
References
-
Isoyama R., Katayama T. Practical performance evaluation of water supply networks during seismic disaster. Lifeline Earthquake Engineering: The Current State of Knowledge, 1981, p. 111-122.
-
Toki K., Sato T. Estimation of damage of water distribution systems by earthquakes. Recent Advance in Lifeline Earthquake Engineering in Japan, 1985, p. 89-96.
-
Muleski G. E., Ariman T., et al. A shell model o f a buried pipe in a seismic environment. Journal of Pressure Vessel Technology, Vol. 101, 1979, p. 44-50.
-
Pao Y. H., Mow C. C. Diffraction of Elastic Waves and Dynamics Stress Concentrations. Crane, Russak and Company Inc., New York, 1973.
-
Hindy A., Novak M. Earthquake response of underground pipeline. Journal of Earthquake Engineering Structure Dynamic, Vol. 7, 1979, p. 451-476.
-
Sancar S., Pao Y. H. Spectral analysis of elastic pulses back scattered from two cylindrical cavities in a solid. Journal of the Acoustical Society of America, Vol. 69, 1981, p. 1591-1596.
-
Davis C. A., Lee V. W. Transverse response of underground cavities and pipes to incident SV waves. Journal of Earthquake Engineering Structure Dynamic, Vol. 30, 2001, p. 383-410.
-
Kattis S. E., Beskos D. E., Cheng A. H. D. 2D dynamic response of unlined and lined tunnels in poroelastic soil to harmonic body waves. Journal of Earthquake Engineering Structure Dynamic, Vol. 32, 2003, p. 97-110.
-
Liu D. K., Gai B. Z., Tao G. Y. Applications of the method of complex functions to dynamic stress concentrations. Wave Motion, Vol. 4, 1982, p. 293-307.
-
Pavic G. Vibrational energy flow in elastic circular cylindrical shells. Journal of Sound and Vibration, Vol. 142, 1990, p. 293-310.
-
Cao H., Lee V. W. Scattering of plane P waves by circular cylindrical canyons with various depth-to-width ratio. Soil Dynamics and Earthquake Engineering, Vol. 9, 1990, p. 141-150.
About this article
This research was financially supported by the National Nature Science Foundation of China, Nos. 11102233 and 51178460.
