The empirical analysis on the portfolio optimization’s effective border

2.1. The concept of mean-variance model

Markowitz (1952) proposed a choice theory of portfolio which can be achieved under conditions of uncertainty [3]: mean-variance model methods. The basic idea of this method is as follows: the expected return of the portfolio is a weighted average of each of the assets constituting the portfolio rate of return to form for the weight ratio of the contribution of assets to the expected rate of return for each portfolio depends on its expected rate of return. Assuming assets 1, 2,…, $N$ on the market, the expected rate of return of asset $i$ is $E\left(r_r\right)$, the variance is ${\sigma }_i$, the covariance of asset $i$ and asset $j$ are ${\sigma }_{ij}$ (or the correlation coefficient is ${\rho }_{ij}$), ($i=$ 1, 2,…, $n$, $j=$ 1, 2,…, $m$). The ratio of invested in asset $i$ is $W_i$, $i=$ 1, 2,…, $N$.

Expected return for the portfolio is Eq. (1):

Multi-asset portfolio variance is Eq. (2):

Covariance is a statistical measure of the relationship between two random variables, it measures two random variables. The covariance assets can be expressed as Eq. (3):

Multi-asset Variance-covariance matrix is Eq. (4):

2.2. The empirical analysis

Based on a large number of transactions recorded on a stock exchange regarding to 20 stocks over six months, we calculated the covariance matrix and average earnings about 20 stocks in the statistical analysis software R language. The average yield in the form of drawing scatter plot was shown in Fig. 1. The average expected rate of return about 20 stocks shows scattered in the figure.

Fig. 1The expected rate of return about 20 stocks

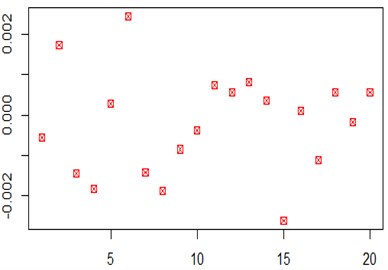
Fig. 2Simulation of 10,000 and 100,000 times of the portfolio’s efficient frontier

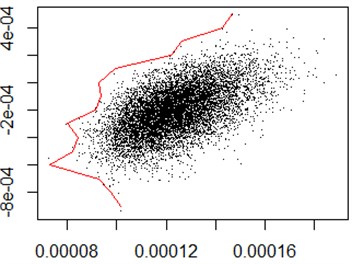
a)

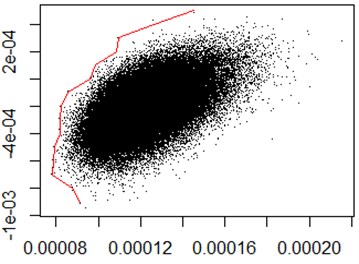
b)

The use of the R statistical software can draw the portfolio’s efficient frontier about 20 stocks. According to the principle of mean-variance model, randomly simulate 10,000 and 100,000 times the weight of the portfolio, the entire portfolio of stippling was drawn in the mean variogram. Select the lowest point of the risk under each expected return that is standard deviation of the minimum point drawn the efficient frontier curve, as shown in Fig. 2. As can be seen from the figure, the implementation process of this method is relatively simple and requires a lot of simulation to get a relatively effective result, and there are some differences between the 10,000 and 100,000 times of the efficient frontier simulation results, it is not very accurate.

3.1. The idea of the simulated annealing algorithm

Simulated annealing algorithm originated in physical annealing process, simulated annealing algorithm was first proposed by Metropolis (1953), and Kirkpatrick (1983) applied it to combinatorial optimization [4]. The principle can be expressed as: annealing mimic natural phenomenon obtained by the similarity of the physical annealing process of the solid material in the general optimization problem. Starting from a certain initial temperature accompanied by declining temperatures, combine with the probability of the sudden jump in the solution space stochastic characteristics to find the global optimal solution. It mimics the physical annealing heating isothermal and cooling process, at a certain temperature, the search randomly change from one state to another state, with the lowest temperature until the temperature drops, the search process to find the global optimal solution. Mathematical ideas can be expressed as follows.

At temperature $T$, the molecule stays in state $r$ satisfy Boltzmann probability distribution, as shown in Eqs. (5) (6):

At the same temperature $T$ the selected two energy $E_1<E_2$, there is Eq. (7):

The main steps of simulated annealing algorithm can be expressed as follows [5]:

Initialization: Given the initial temperature t=t0;

Randomly generated initial states=s0;

k=0;

Repeat

Repeat

Generate new state: sj=Generate(s)；

If min {1,exp [-(C(sj)-C(s))/tk]}>=random[0,1] s=sj;

Until meet the sampling stability criteria;

Return temperature tk+1=update(tk) and make k=k+1;

Until Algorithm terminates meet the criteria;

The output of the algorithm search results.

3.2. The empirical analysis

Based on the basic idea of simulated annealing method, it needs to determine the initial temperature and internal cycles, these two parameters are the most important parameters directly determine the effect of the number of cycles and optimize the algorithm. If the initial temperature is set too low, the temperature drop less times, leading to the possibility of searching the global optimum to be less likely. On the contrary, if the initial temperature is set too high, the temperature drop more times, the possibility to search the global optimum is greater. However the increase will reduce the number of iterations of the feasibility and effectiveness of the algorithm, therefore it need several attempts to determine the efficient frontier of simulated annealing method to select the most suitable parameter control cycles and results.

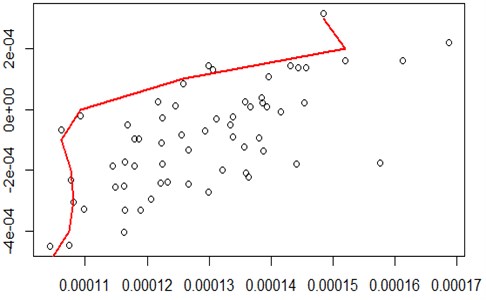
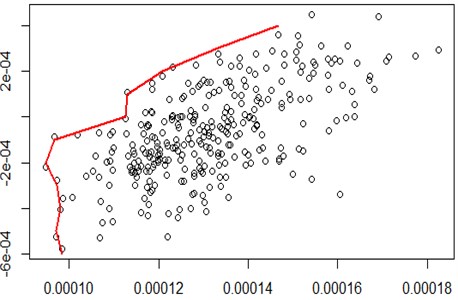
When the initial temperature is set to 10000, inner cycles is set to 10, using R statistical software to draw the effective boundaries was shown in Fig. 3. It can be seen from the figure, the points of 20 stocks portfolio is dispersed, the number of less cycles makes efficient frontier not obvious.

Fig. 3Initial temperature of 10000, 10 cycles of simulated annealing method for the efficient frontier

When the initial temperature increase to 100000, the number of cycles 50, the points of 20 stocks portfolio is more concentrated stock, optimized results were better. The effective boundary was shown in Fig. 4.

Fig. 4Initial temperature of 100 000, 50 cycles of simulated annealing method for the efficient frontier (to optimize the efficient frontier)

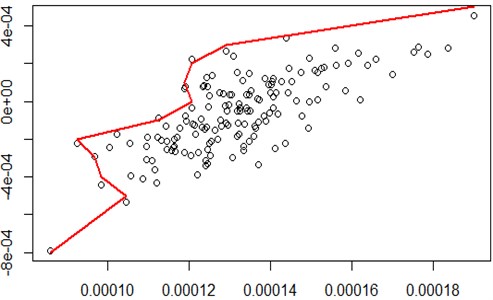
When the initial temperature is up to 1 million, the number of cycles 100, the points of 20 stocks portfolio concentration is not very good, there is no effective border compared to Fig. 4, as shown in Fig. 5, therefore, according to 20 stocks portfolio optimization effective border, the efficient frontier select best shown in Fig. 4.

Fig. 5Initial temperature of one million, 100 cycles of simulated annealing method for the efficient frontier