Vortex signal detection method with stochastic resonance based on adaptive coupled feedback control

1. Introduction

Stochastic resonance (SR) [1] is the nonlinear phenomena, which is caused by the synergistic effect from weak periodic signal and nonlinear system with the medium of noise. To realize SR, especially to enhance SR effect and improve SNR, is not unconditional. The input signal, noise and nonlinear systems need to meet certain matching conditions. Only controlled effectively, SR is generated and strengthened. Many scholars [2-4] have done a lot of work to control SR. The coupled bistable system is composed of two signal bistable systems with nonlinear coupling by Min Lin et al. [5]. Then SR is achieved by using the coupling feedback control.

In the form of closed loop control, it uses output feedback, while the parameter-fixed system is as a controlled object, the coupling module and parameter-adjustable bistable system are as a feedback controller, with the coupled coefficient and the adjustable parameters of the bistable system as control variables. Also, SNR is selected as the performance index of coupled feedback control system. Artificial fish swarm algorithm [6, 7] has advantages which can overcome the local extremum and obtain the global extremum well. So it is used to search the value of control variables for the optimal system performance index adaptively. Consequently, the optimal control of the coupled bistable SR is realized. The vortex shedding frequency can be obtained accurately.

2. Basic theory

The classic SR can be described as:

where $a_0$ and $b_0$ are the bistable system parameters, $A\mathrm{c}\mathrm{o}\mathrm{s}wt$ is the periodic signal with amplitude $A$ ($A\ll 1$) and frequency $w$, $\xi \left(t\right)$ denotes Gaussian white noise with zero mean, meeting the conditions: $\left[\xi \right(t\left)\xi \right(0\left)\right]=2D\delta \left(t\right)$, in which $D$ indicates the noise intensity.

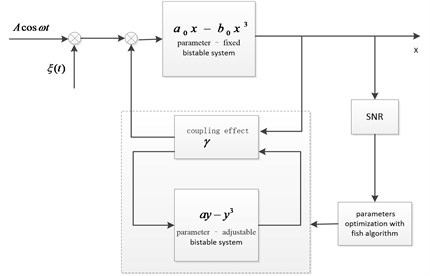
The coupled bistable system is composed of two single bistable systems by means of nonlinear coupling. The parameters of one system ($a_{0}x–b_0{x}^3$) are fixed, and the parameters of the other ($ay-y^3$) are adjustable. The relationship between variables and parameters of coupling control process can be drawn as follow:

where $r$ is the coupling coefficient between two bistable systems, $a$ is the bistable system tunable parameter, and $x\left(t\right)$, $y\left(t\right)$ are the bistable system variables. With the change of coupling coefficient $r$ and control system adjustable parameter $a$, the coupling bistable system will present different SR characteristics.

The coupling feedback control method is based on artificial fish swarm algorithm. The optimal control of the coupled bistable SR is taken place by adjusting control variables. The schematic diagram has been described as Fig. 1.

Fig. 1Block diagram of coupling feedback control based on artificial fish swarm algorithm

3. SR based on adaptive coupled feedback control

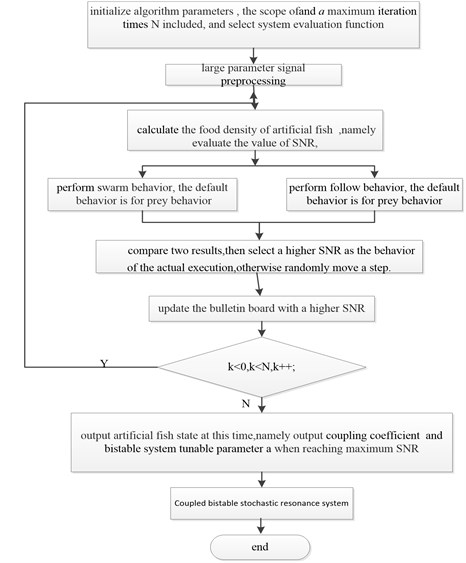
Status of individual fish is $X=(x_1,x_2,x_3,\dots ,x_n)$, where the optimized variables are $x_i$ ($i=$1, 2, 3,…, $n$). The food density of artificial fish in the current position is $Y=f\left(x\right)$, in which $Y$ is the objective function value, $Visual$ is the perception distance between individual fish, $Step$ is the moving step length of individual fish, $\delta$ is the crowded degree factor. There are three behavior: prey behavior, swarm behavior and follow behavior. According to the problems found in the practical application, we can select one or several behavior. Artificial fish swarm algorithm is used to adjust coupling coefficient $r$ and bistable system tunable parameter $a$ adaptively. Finally, the optimal control of the coupled bistable stochastic is realized and enhanced, as is shown in Fig. 2. The implementation steps are written as follow:

(1) Setting the parameters of the artificial fish swarm algorithm: such as artificial fish population size $M$, the largest iteration times $N$, perception distance $Visual$, largest moving step length $Step$, crowded degree factor $\delta$. If end index for the optimal value in step $N$ still did not change, it doesn’t converge. Then do signal preprocessing and initialize the fish.

(2) Setting bulletin board: calculate the food density of artificial fish in the current position of initial artificial fish, namely evaluate the value of SNR, compare different SNR, and select the maximum into the bulletin board.

(3) Behavior selection and updating the bulletin board: each of the artificial fish simulates swarm behavior and follow behavior. Select a higher SNR as the behavior of the actual execution, and the default behavior is for prey behavior. Then update the bulletin board with the better result.

(4) Judgment of the end condition: whether iteration time $k$ has been equal to the maximum number $N$. If so, perform step (5); otherwise, perform step (3).

(5) Optimal output of bulletin board: coupling coefficient $r$ and bistable system tunable parameter $a$ are applied to a coupled bistable system when it is equal to the maximum SNR. The system can generate SR and achieve weak signal detection.

Fig. 2SR based on adaptive coupling feedback control

4. Numerical simulation and results

When $a_0=$1, $b_0=$1, low frequency periodic signal with amplitude $A=$ 0.2 and frequency $f_0=$ 0.01, noise intensity $D=$ 0.15, we cannot see weak periodic signal because of the strong noise from Fig. 3. Aiming at the single system ($r=$ 0), characteristic frequency cannot be detected, as is shown in Fig. 4.

Fig. 3Input time domain waveform

Fig. 4Output power spectrum of the single system (r= 0)

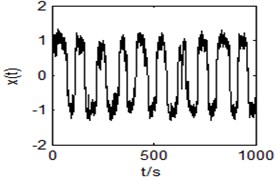
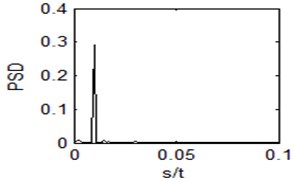
When $r=$1 and $a=$ 1, the input signal is imported into coupled bistable system, then SR will appear. We can see an obvious spectral peak in Fig. 5. By calculating, the SNR is 18.73012.

We seek coupling coefficient $r$ and bistable system tunable parameter $a$ by using artificial fish swarm algorithm. The parameters are shown as below: $fishnum=$ 100, $Visual=$ 2.5, $\delta =$ 0.618, $step=$ 0.05. It will iterative 200 times to find $r$ and $a$ to maximize the SNR. Optimal result is $r=$ 0.9735, $a=$ 1.0335. The coupling coefficient $r$ and the bistable system adjustable parameter $a$ are set to optimize the result, at the same time, the input signal is applied to the coupled bistable system. Then we can see obvious phenomenon of SR, as is shown in Fig. 6, in which SNR is 21.6736. Compared to Fig. 5, the spectral peak increases a lot. Also SNR is improved by 16 %.

Fig. 5Output time domain waveform and power spectrum of the bistable system with r= 1, a= 1

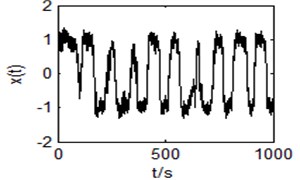
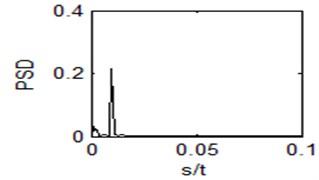
Fig. 6Output time domain waveform and power spectrum of the bistable system with r= 0.9735, a= 1.0335

5. Vortex signal detection

When the flow is 5.10 m³/h, the input signal of vortex flowmeter is analyzed with SR. For the large frequency signal in engineering, it should be preprocessed to meet the requirement of small parameters of the adiabatic approximation theory with twice sampling. Preprocess vortex signal submerged in the strong noise and chose sampling frequency $f_s=$ 2000, sampling number $N=$ 15016, frequency compression ratio $R=$ 1250, so the frequency of twice sampling is $f_{sr}=f_s/R=$ 2000/1250 $=$ 1.6 Hz.

Fig. 7 displays the time domain waveform and power spectrum generated by a small flow vortex signal. Noise in the time domain waveform is strong and completely covers the characteristics of the vortex signal, leading to a lower SNR. Therefore, it is difficult to detect the apparent spectral peak in the characteristic frequency of vortex signal.

Fig. 7Input time domain waveform and power spectrum of the original vortex signal

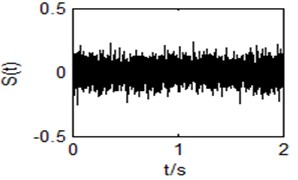
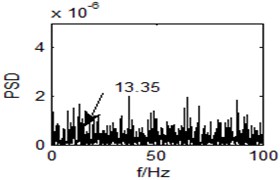
Fig. 8Output time domain waveform of the single system (r= 0)

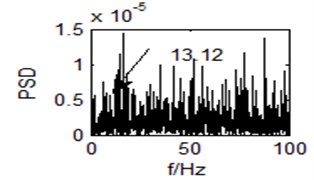
Fig. 9Output time domain waveform of the bistable system (r= 1)

In Fig. 8 and Fig. 9, the phenomenon of SR is not obvious. The corresponding spectral peak is hardly found, either.

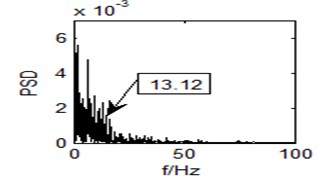
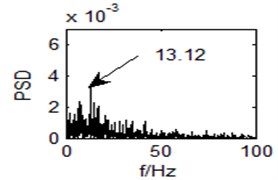
In the experiment, the parameters are: $fishnum=$ 100, $Visual=$ 2.5, $\delta =$ 0.618, $step=$ 0.05. Then it will iterative 200 times to find $r$ and $a$ to maximize the SNR. Optimal result is $r=$ 0.8198, $a=$ 0.9438. Obviously, we can see a spectral peak at the point 13.12 Hz, as is shown in Fig. 10. The vortex shedding frequency for the theoretical value is 13.35 Hz. It is a lot higher than the surrounding components, and is very outstanding in the whole power spectrum. Accordingly, the method with SR based on adaptive coupled feedback control has effectively realized small flow vortex signal detection.

Fig. 10Output power spectrum of the bistable system with r= 0.8198, a= 0.9438

6. Conclusions

Combining the coupled bistable system SR with artificial fish swarm algorithm, the vortex signal detection method with SR based on adaptive coupled feedback control is put forward in the article. It controls the generation of SR with coupling, and then enhances resonance effect with the optimization of control parameters. Numerical simulation and vortex signal detection manifest that weak periodic signal can be enhanced, the output SNR can be improved, and characteristic frequency can be successfully extracted. As a novel solution to improve the adaptability and achieve small vortex signal detection, it is feasible and effective in vortex signal detection. The method can also be used to detect weak signal submerged in the strong noise in other fields, such as mechanical fault diagnosis, the vibration signals of the metal cutting process analysis, and has better application prospects.