Multi frequency weak signals detection based on under-sampling bistable stochastic resonance

1.1. Stochastic resonance model

In general, stochastic resonance model can be divided into three parts: input signal; noise; nonlinear system. When the nonlinear system is subjected to the synergistic effect of the input signal $s\left(t\right)$ and noise $\mathrm{\Gamma }\left(t\right)$, reach or exceed a certain threshold system, the noise energy can enhance the signal energy, and stochastic resonance phenomenon appears.

Fig. 1Stochastic resonance model diagram

1.2. Bistable system

The common nonlinear systems include heterodyne stochastic resonance model, multi-scale noise regulation model, bistable stochastic system model and adaptive stochastic resonance model, among which the bistable stochastic system model is widely used in many research fields, such as physics, chemistry and communication, etc. Secondly, the research results of bistable system are still suitable for multi-stable system such as three-stable and four-stable. When the system inputs signals and noise, neither energy is generated nor consumed. It is only transmitted between the input signal and noise, and ultimately between the output signals. The bistable stochastic resonance model can easily improve the SNR by adjusting intensity and system parameters.

Given a bistable system affected by white noise $\mathrm{\Gamma }\left(t\right)$ and external periodic driving forces $A\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\Omega }t$, the Langevin equation is following:

where, the statistical properties of white noise are $〈\mathrm{\Gamma }\left(t\right)〉=0$, and $E\left[\mathrm{\Gamma }\left(t\right)\mathrm{\Gamma }(t+\tau )\right]=2D\delta \left(\tau \right)$, $A\mathrm{c}\mathrm{o}\mathrm{s}\omega t$ is the external periodic driving force. The nonlinear external force field $f\left(x\right)=ax-b{x}^3$ is introduced into the above equation, and the potential function is Eq. (2):

where, $x_m=\pm {\left(a/b\right)}^{1/2}$ respectively, are the two stable equilibrium points of Eq. (2), which are separated by a barrier of high $\mathrm{\Delta }V=a^2/4b$. The analysis shows that when the amplitude of the input signal is greater than the threshold value $A_c=\sqrt{4a^3/27b}$, the particle can cross the barrier.

It is difficult to calculate the macro equation of this formula by statistical averaging of nonlinear systems. Considering that the noise has a certain energy, under appropriate conditions, the active Brown particles will break through the binding of the potential barrier under the effect of the noise energy, realize the energy transfer, increase the output SNR, and appear Stochastic resonance phenomenon. When a bistable system is subjected to both signal and random noise, the output SNR can be improved by adjusting the system parameters.

The probability distribution function in Eq. (1) is $\rho (x,t)$, and the FPE equation of the probability distribution function is as below:

Eq. (3) is a second-order partial differential equation, here $\rho (x,t)$ is a Markov process, and the initial condition in the equation is $\rho (x,t_0|x_0,t_0)=\delta (x-x_0)$, on the right side, there are terms $-\frac{\partial }{\partial x}\left[A\mathrm{c}\mathrm{o}\mathrm{s}{\omega }_{0}t\rho \right(x,t\left)\right]$, so the analytical results of the system cannot be found, and the following research will carry out numerical simulation.

1.3. SNR and SNRI

In order to quantitatively characterize the relationship between input signal and noise in the detection system, SNR and SNRI are important indicators to study the detection system. The SNR refers to the ratio of the effective value S of a signal to the effective value N of noise, reflecting a ratio relationship between signal components and noise components. The expression is:

where $S\left(\omega \right)$ is power spectral density, $S_N\left(\omega \right)$ is the noise intensity. Usually, the output SNR is a local value, it can be maximized by adjusting the system parameters and noise intensity. Therefore, how to improve SNR is the key to signal detection. The ability of a system to suppress noise is usually measured by SNRI, which $SN{R}_{gain}=SN{R}_{out}/SN{R}_{in}$ is an expression for SNRI. $SN{R}_{out}$ is the SNR of the output signal. The larger SNRI of the input signal, the stronger the system's ability to suppress noise. In this paper, the SNR is used to describe the Stochastic resonance phenomenon. Based on the adiabatic approximation theory and the output power spectrum of the system, the approximate expression of the output SNR of Eq. (1) is as below [18]:

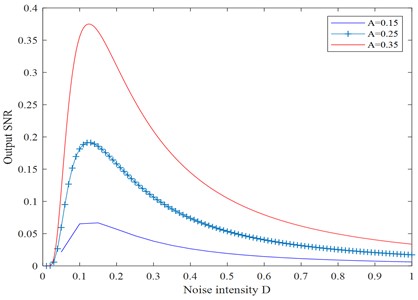
Here, we take $a=b=1$, the potential barrier $\mathrm{\Delta }V=\text{0.25}$. Fig. 2 shows the numerical calculation results of Eq. (5). It can be seen that when other parameters and noise intensity of are constant, an increase in signal amplitude can bring about a higher output SNR; When other system parameters and signal amplitude are fixed, as the noise intensity increases, the SNR in Fig. 2 shows a trend of first rapidly increasing and then gradually decreasing.

Fig. 2SNR with noise intensity D under different signal amplitudes

2.1. Power spectrum of noise response

According to the adiabatic approximation theory, the power spectrum of pure noise response in a bistable system is as follows [19]:

where $f=\frac{1}{T}=\frac{a}{\sqrt{2}\pi b}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{a^2}{4D{b}^2}\right)$ is the average first-pass frequency, substitute into Eq. (6), and simplify:

The power spectrum of the noise response decreases with the increase of frequency in a hyperbolic function curve, indicating that the noise spectrum energy is concentrated in the low-frequency band. In this paper, Matlab software is used to calculate and analyze the detection of multi frequency weak signals according to the fourth-order Runge-Kutta algorithm.

2.2. Stochastic resonance of multi frequency weak signal superposition

The simulation model of the single-frequency weak signal system is improved, and the signals are extended to three signals, and then the appropriate system parameters $a$, $b$ and noise intensity $D$ are selected for simulation experiments, where $a=\text{1}$, $b=\text{1}$, $D=$0.5, sampling frequency is 10 Hz, the threshold of the system is $A_c=\sqrt{4a^3/27b}\approx \text{0.3849}$, take the input multi-frequency cosine signal amplitude $A_i=\text{0.5}$, $s\left(t\right)=\sum _{i=1}^3{A}_i\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi f_{i}t\right)$.The frequencies are $f_1$= 0.01 Hz, $f_2$= 0.03 Hz, and $f_3$= 0.05 Hz in turn. The spectrum diagrams of signal input and output are shown in Fig. 3 and Fig. 4.

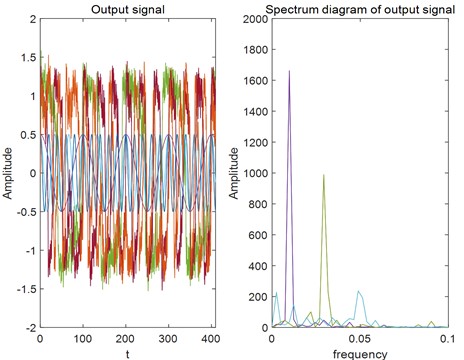
As can be seen from time domain/spectrum diagram of the output of three signals in Fig. 4, stochastic resonance phenomenon appears in the system. Signals in the low-frequency concentrated region are significantly amplified when passing through the bistable stochastic resonance system, while signals in the relatively high frequency region are relatively weak, and the energy of noise spectrum is concentrated in the low-frequency signal section, which further verifies the rule given by Eq. (7).

Fig. 3Time domain/spectrum diagram of three input signals

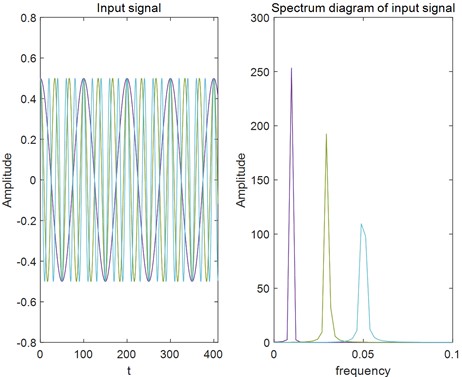
Fig. 4Time domain/spectrum diagram of the output of three signals

3.1. The theoretical principle of under-sampling stochastic resonance

The premise of application of adiabatic approximation theory is low frequency weak signal. When large parameter signal is encountered in signal detection, it cannot meet the requirements of adiabatic approximation theory. To overcome this limitation, a weak signal detection model based on under-sampling stochastic resonance is proposed in this paper.

According to the weak signal detection method principle of under-sampling stochastic resonance, the large parameter signal is under-sampled by appropriate scale coefficients, so that the under-sampling signal is still a periodic signal, and its frequency conforms to the adiabatic approximation theory. Then, the weak sampled signal is detected through stochastic resonance effect. in the end, the scale inverse transformation of the under-sampled signal is carried out to realize the recovery of the large parameter signal. Different from other scaling methods, this algorithm directly under-samples the input signal, which will reduce the sampling rate and complexity. which is widely applied and easy to implement.

3.2. Weak signal detection algorithm based on under-sampling stochastic resonance

The frequency of the input signal with a large parameter of single is $f$, the initial phase is ${\varphi }_0=0$, the under-sampling scaling coefficient is $N$, the corresponding sampling interval is defined as $T_s=1/(Nf+f)$, and the under-sampling sequence is Eq. (8):

where $f_s=f/(N+1)$. This is obvious that the under-sampled signal $s_n$ in Eq. (8) is still a periodic signal. When the frequency of the input signal $f$ does not meet the constraints of the adiabatic approximation theory, an appropriate under-sampling scale factor $N$ can be selected to transform high-frequency input signal into a smaller parameter. According to stochastic resonance theory, when the input signal and noise synergize to produce stochastic resonance, the output signal is a similar cosine signal $s_n$. For the under-sampled signal, the output signal is solved numerically using a fourth-order Runge-Kutta discretization method. The approximate expression is given in Eq. (9) [20]:

where $A\text{'}$ is the amplitude of the output signal, and $\phi$ is the additional phase difference generated by the nonlinear processing time delay. Therefore, according to the previous method, frequency spectrum can be analyzed to extract the under-sampling signal frequency $f_s$. The frequency of the original input signal can be restored by formula $f=f_s\times (N+1)$.

3.3. Simulation result

Based on the previous weak signal detection method and principle analysis of under-sampling stochastic resonance, the signals with large parameters are first under-sampled at an appropriate sampling rate, So that they are still periodic and meet the theoretical conditions of adiabatic approximation. Now select the input signals.

$s\left(t\right)=\sum _{i=1}^3{A}_i\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi f_{i}t\right)$, system parameter $a=$ 1, $b=$ 3, $A_i=$ 0.5, $f_1=$ 5 Hz, $f_2=$ 25 Hz, $f_3=$ 45 Hz, $D=$0.6, sampling frequency $f_s=$ 10 Hz, $N=$500.

Fig. 5Noiseless/noise signals with mixed frequency input

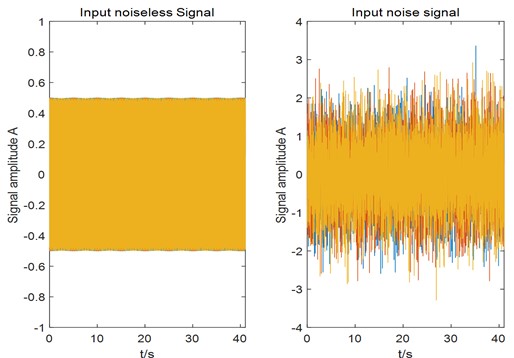
Fig. 6Spectrum of the input under-sampling and noisy mixed frequency signal

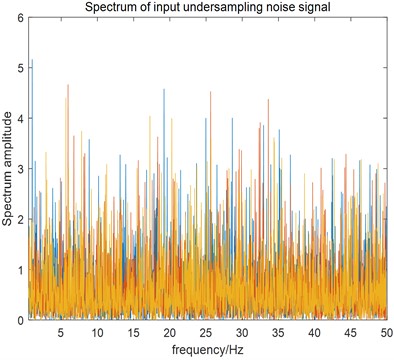
According to the requirements of the sampling interval of under-sampling, select scale transform coefficient $N=$ 500, and then the under-sampling signal is analyzed by FFT spectrum. It is found that the useful signal is almost completely drowned out by noise, and the multi-frequency mixed signal cannot be recognized.

Fig. 7Time domain/spectrum diagram of the output signal after under-sampling

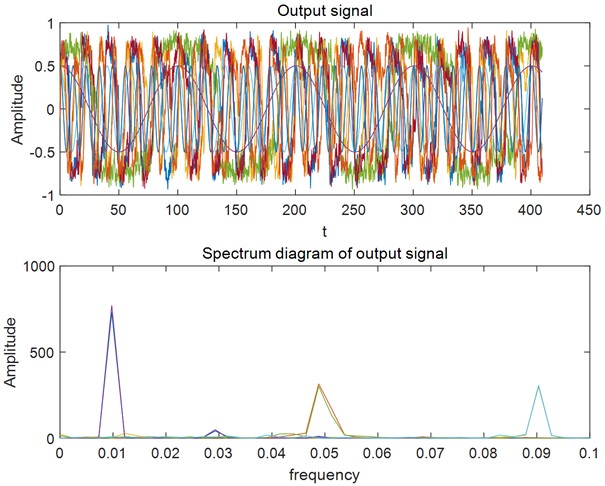
As can be seen in Fig. 7, the stochastic resonance phenomenon appears in the nonlinear bistable system. Within the allowable error range, the amplitude of the output signal has obvious spectral peaks at the three frequencies, which are $f_1=$ 0.0098 Hz, $f_2=$ 0.049 Hz, $f_3=$ 0.09 Hz in turn, and the signals to be detected can be successively restored by using the formula $f=f_s\times (N+1)$, so that the multi-frequency $f_1=$ 4.91 Hz, $f_2=$ 24.55 Hz, $f_3=$ 45.09 Hz, mixed signals submerged in high noise at the input can be detected and identified one by one. Then it is verified that the high multi-frequency weak periodic signal in the white noise is detected based on under-sampled stochastic resonance.