Analysis of weak faults of planetary gears based on frequency domain information exchange method

2.1. Stochastic resonance principle

The SR system can be described by three components: a nonlinear system, Gaussian random noise, and periodic signal. When the synergistic effects of all the three components are optimal, the signal can be clearly enhanced by SR. In this paper, the bi-stable SR system is analyzed. The Langevin equation can be written as:

where $a$ and $b$ are the bi-stable system parameters, $s_p\left(t\right)=A\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi f_{0}t\right)$ is a periodic input signal, $A$ is the amplitude of the input signal, $f_0\mathrm{}$is the characteristic frequency of the signal, $n\left(t\right)$ is Gaussian white Gaussian random noise, $E\left[n\left(t\right)\right]=$ 0, $E\left[n\left(t\right)n(t-\tau )\right]=2D\delta \left(\tau \right)$, and $D$ is the Gaussian random noise intensity. The potential function of the bi-stable system is usually expressed as:

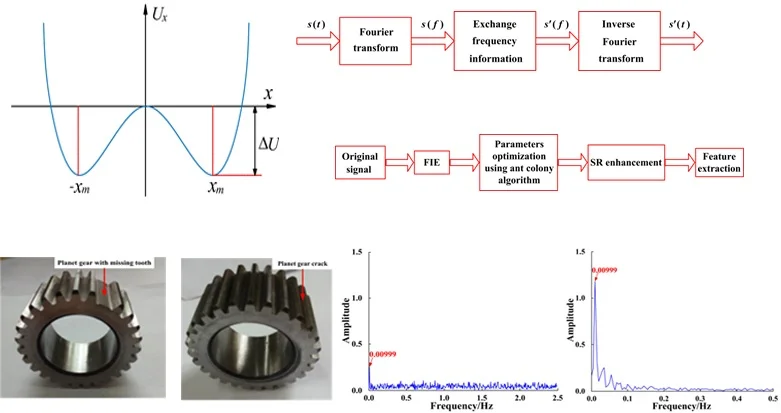
An illustration of the potential well concept is shown in Fig. 1. The bi-stable function has an unsteady state $x=$ 0 two steady-states $\pm x_m(x_m=\sqrt{a/b})$, and barrier height $\mathrm{\Delta }U=a^2/\text{4}b$. When the input signal is zero, the system is in the steady state. Moreover, when the input signal $s_p\left(t\right)$ is weak, sufficient energy does not exist to overcome the barrier, therefore the signal can only move within a single potential well. However, when a certain intensity of Gaussian random noise $n\left(t\right)$ is added to the weak input signal, a portion of the additional Gaussian random noise energy is transferred to the signal and the signal can overcome the barrier. Thus, a transition between the two steady states occurs, that is, an SR phenomenon occurs.

Fig. 1Potential function of bi-stable SR system

2.2. Optimization of adaptive stochastic resonance parameters

According to the principles of SR, the potential barrier is an important factor affecting the SR phenomenon. Barrier height $\mathrm{\Delta }U$ can be determined by selecting the values $a$ and $b$. Therefore, the choice of system parameters $a$ and $b$ plays a pivotal role in whether SR occurs. To achieve optimal signal processing with SR method, it is particularly important for the system parameters to be adaptively optimized. In general, SR parameter optimization methods use a single system parameter as the optimization objective while all other parameters remain unchanged. Then, the influence of the parameter on the system output is discussed. However, these parameter optimization methods are local optimization methods that ignore the interaction between various parameters of the SR system. Therefore, only relative optimal values of the SR system parameters can be obtained [19].

In this paper, to obtain the globally optimal solution of the SR system parameters and to achieve the best signal processing effects using the SR method, an adaptive SR method is proposed that simultaneously optimizes parameters $a$ and $b$ using the ant colony algorithm [20, 21].

2.3. Verification of the adaptive stochastic resonance method

2.3.1. Simulation signal verification

An expression of the input signal can be given as:

3

$s_1\left(t\right)=A_1\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi f_{01}t\right)+nois{e}_1\left(t\right),$

where $A_1=$ 0.03, $f_{01}=$ 0.05 Hz, and the Gaussian random noise intensity of $nois{e}_1\left(t\right)$ is 0.25. A sampling frequency $f_{s1}=$ 20 Hz is assumed with $N_1=$ 2000 sampling points.

First, the traditional parameter optimization method was used to optimize a single parameter of the system. One parameter was fixed, $a=$ 1, and $b$ was optimized. The simulation signal spectrum is presented in Fig. 2. Then the other parameter was fixed, $b=$ 1, and $a$ was optimized. The simulation signal spectrum is shown in Fig. 3. Finally, the proposed ant colony algorithm was applied to adaptively optimize the parameters $a$ and $b$ simultaneously, and the resulting signal spectrum is illustrated in Fig. 4.

Comparing Fig. 4 with Figs. 2 and 3, it can be seen that the proposed ASR method is capable of extracting the signal characteristics more effectively. Thus, the effectiveness and superiority of the proposed method is verified.

Fig. 2Simulation signal spectrum when parameter a is fixed

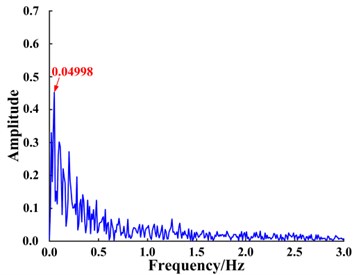
Fig. 3Simulation signal spectrum when parameter b is fixed

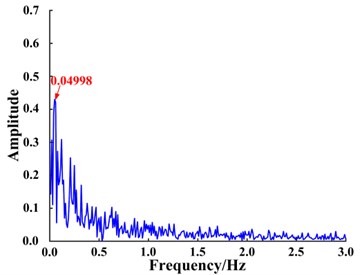
Fig. 4Signal processed using the proposed adaptive SR method

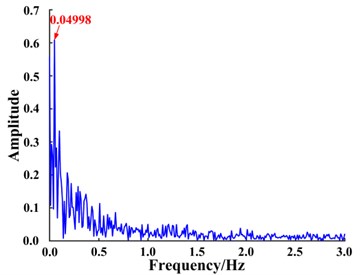
2.3.2. Test signal verification

The adaptive SR method proposed in this paper was applied to process the envelope signal of the fault signal collected from of a planetary gear with a missing tooth. A detailed description of the procedure is provided in Section 4.

As shown in Fig. 5, the fault signal was not successfully extracted as the resulting signal does not contain the fault characteristics. The poor result is owing to the small parameter limits of SR [22, 23]. The method must be improved in order to successfully extract features from signals under real conditions. A detailed description of the adiabatic approximation of small parameters for SR is provided and an improved adaptive SR method is presented that overcomes the small parameter limits, i.e., an adaptive stochastic resonance fault diagnosis method based on frequency information exchange.

Fig. 5Signal processed using the adaptive SR method

3.1. Small-parameter conditions of SR adiabatic approximation

The function [24] representing the response amplitude $\stackrel{-}{x}$ of a bi-stable SR system that varies with Gaussian random noise intensity $D$ is given by:

however, real engineering signals do not satisfy the small-parameter conditions of the adiabatic approximation, that is, the characteristic frequency of the engineering signal cannot satisfy the condition $f_0\ll$ 1. Therefore, overcoming the limitations of the small-parameter condition of the adiabatic approximation is an urgent problem. If solved, the signal to be processed would be able to undergo the SR phenomenon, thus making it possible to successfully process real engineering signals using the SR method. In this paper, a method based on frequency information exchange (FIE) is proposed to solve the problems associated with the small-parameter conditions of the SR adiabatic approximation. The method is discussed in detail in the next section.

Fig. 6Variation of response amplitude x- of bi-stable SR system with Gaussian random noise intensity D for different characteristic frequencies f0

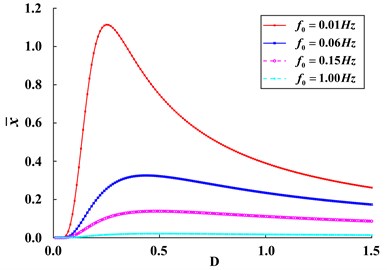
3.2. Mechanism of frequency information exchange

The FIE method involves exchanging frequency information at the characteristic frequency point of the original signal and reference frequency point to obtain a new signal.

A flow chart of the FIE method is presented in Fig. 7. First, the original time domain signal $s\left(t\right)$ is transformed using the Fourier transform to obtain a frequency domain signal $s\left(f\right)$. Then, the frequency information at the characteristic frequency $f_0$ and reference frequency $f_1$ are exchanged. Now, the reference frequency $f_1$ contains the amplitude and phase information at the characteristic frequency $f_0$. After the frequency domain exchanged, the signal is written as $s\mathrm{\text{'}}\left(f\right)$. Finally, the signal $s\mathrm{\text{'}}\left(f\right)$ can be transformed using the inverse Fourier transform to obtain a new time domain signal $s\mathrm{\text{'}}\left(t\right)$.

Fig. 7Flowchart of frequency information exchange (FIE) method

The essence of FIE lies in modulating the upper and lower single sideband signals of the reference frequency signal and characteristic signal, respectively [24]. Letting the reference frequency signal $s_1\left(t\right)=A_1\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{1}t+{\phi }_1)$, the characteristic signal $s_t\left(t\right)=A_t\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{t}t+{\phi }_t)$, and $\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{c}t\right)$ represent the carrier signal, the reference frequency signal modulated on the upper single sideband is:

Furthermore, the characteristic signal modulated on the lower single sideband is:

where $H\left[\mathrm{*}\right]$ represents the Hilbert transform. Letting ${\omega }_c={\omega }_t-{\omega }_1$, after a single sideband signal modulation the frequency of the reference frequency signal $s_1\left(t\right)$ is converted to ${\omega }_t$, the frequency of the characteristic signal $s_t\left(t\right)$ is transformed to ${\omega }_1$, and the amplitude and phase information of each signal remain unchanged. That is, frequency information exchange between $s_t\left(t\right)$ and $s_1\left(t\right)$ occurs.

3.3. Adaptive stochastic resonance method based on frequency information exchange

A flowchart of the FIE-ASR method proposed in this paper is presented in Fig. 8 and the specific steps for implementing the method are as follows:

(1) Process the original signal using the FIE method. This involves exchanging frequency information between the signal characteristic frequency of interest and a reference low frequency. The exchanged signal now meets the small-parameter requirements of the adiabatic approximation.

(2) Optimize the SR system parameters $a$ and $b$ using the adaptive ant colony algorithm. Use the SNR of the system output signal as the evaluation function of the ant colony algorithm.

(3) Input the transformed signal from Step (2) into the SR system along with the optimized system parameters $a$ and $b$ from Step (3). The feature signal is now enhanced, and the signal features can be extracted.

Fig. 8Flowchart of the adaptive stochastic resonance method based on frequency information exchange (FIE-ASR)

3.4. Simulation analysis

To verify the effectiveness of the FIE-ASR method, the method was used to process a simulated signal. The input signal can be expressed as:

where $A_2=$ 0.25, $f_{02}=$ 1.2 Hz, and the Gaussian random noise intensity of $nois{e}_2\left(t\right)$ is 0.25. A sampling frequency of $f_{s2}=$ 5 Hz was considered with $N_2=$ 1000 sampling points. The bi-stable system parameters were $a=$ 1, $b=$ 1.

Signal $s\left(t\right)$ was input into the bi-stable SR system. The time domain waveform of the signal is shown in Fig. 9(a) and the corresponding response is shown in Fig. 9(c). The system is bi-stable; therefore, the input signal does not undergo the SR phenomenon. The input signal spectrum shown in Fig. 9(b) and the response spectrum of the bi-stable system shown in Fig. 9(d), demonstrate that the amplitude at the characteristic frequency of the input signal $f_0$ is not enhanced but instead considerably weakened. The reason for this phenomenon is that the characteristic frequency of the input signal, $f_0=$ 1.2 Hz, does not meet the small-parameter conditions required for SR.

Fig. 9Response of bi-stable system based on large-parameter input signal

a) Input signal waveform

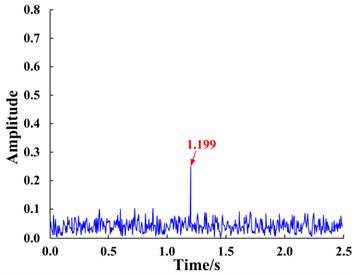
b) Input signal spectrum

c) Output signal waveform

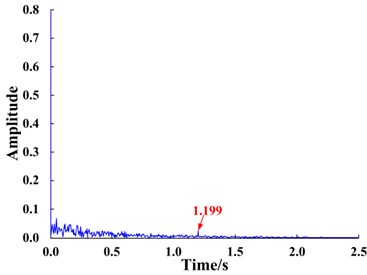
d) Output signal spectrum

The FIE-ASR method proposed in this paper was used to process the same signal. First, the characteristic frequency information at $f_0=$ 1.2 Hz of the input signal was exchanged with the frequency information at the lower reference frequency $f_1=$ 0.01 Hz. The transformed signal spectrum is shown in Fig. 11(b). It can be seen that the amplitude and phase information of the reference frequency exist at the characteristic frequency $f_0=$ 1.2 Hz, thereby satisfying the small-parameter conditions of SR. The transformed frequency domain signal was subjected to inverse Fourier transformation to obtain the post-FIE time domain signal, as shown in Fig. 11(a). Taking the SNR of the output signal of the bi-stable system as the function to evaluate, the system parameters, $a$ and $b$, can be adaptively optimized using the ant colony algorithm. The ranges of initial parameters of the system are 0 < $a$ < 10, 0 < $b$ < 10 and were each divided into 10 equal parts. For the optimization, the pheromone evaporation coefficient was 0.9, the number of ants was 100, accuracy was set to 0.03, and the maximum number of iterations was 20. Results of the parameter optimization are presented in Fig. 10.

The optimized parameters were input into the bi-stable system and the time domain signals were found to be enhanced after FIE. The response waveform and spectrum of the bi-stable SR system are shown in Fig. 11(c), (d).

The SR phenomenon produced by the system is significant, as seen in Fig. 11(c), (d). Furthermore, the amplitude of the characteristic frequency $f_1=$ 0.01 Hz is much larger than (4.7 times) the amplitude of the original signal, thus the original signal is clearly enhanced and amplified, which verifies the effectiveness of the proposed method.

Fig. 10Results of system parameter optimization based on ant colony algorithm

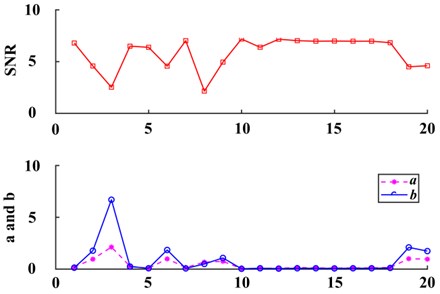
Fig. 11Results of applying the FIE-ASR method to the simulated signal

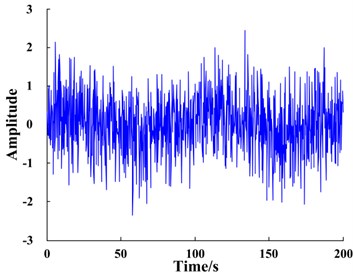
a) Input signal waveform processed by FIE

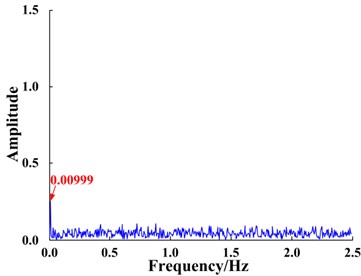
b) Input signal spectrum processed by FIE

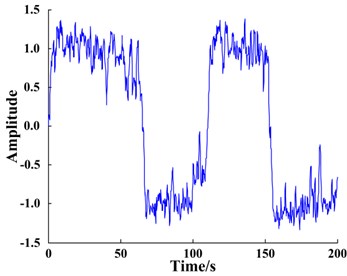
c) Waveform of system response

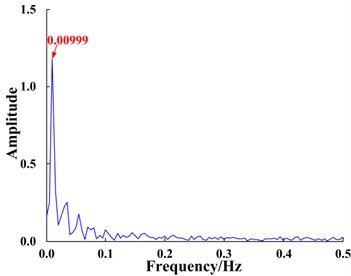
d) Spectrum of system response

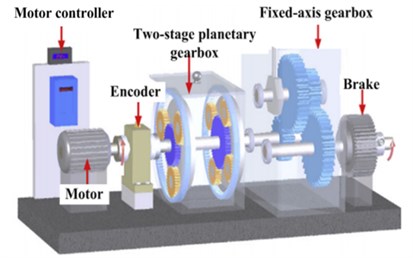
4.1. Experimental platform

A planetary gearbox fault diagnosis test rig (including experimental systems and three-dimensional models of the experimental systems [21]), as shown in Fig. 12, was used to validate the proposed method.

The planetary gearbox is comprised of a sun gear, three planetary gears, a planetary carrier, and a ring gear. The sun gear is located at the input end and the planet carrier is at the output end. Parameters and characteristic frequencies of the planetary gearbox are presented in Table 1. Various acceleration sensors were arranged on the housing of the gearbox to collect the vibration signals. In this paper, the signal obtained from a sensor fixed to the ring gear located on the front-side of the lower box is analyzed. The sampling frequency of the signal was 51.2 kHz and the sampling time was 200 s. The vibration signals of the planetary gearbox system were collected throughout the experiment under various conditions, including no fault (normal operating conditions), as well as fault conditions such as a cracked planet gear crack or planetary gear with a missing tooth. Photos of the gear faults are shown in Fig. 13. To better simulate real operating conditions, strong noise was artificially introduced into the collected signal data. The time domain waveforms, spectra, and envelope spectra of the original signals are shown in Fig. 14. It can clearly be seen that strong noise disguises the weak signals of the planetary gearbox. In addition, the fault characteristics cannot be isolated regardless of whether the weak signal characteristics are found within the time-domain waveforms, spectra, or envelope spectra; therefore, failure of a planetary gear cannot be predicted without an appropriate signal extraction method.

Fig. 12Planetary gear experimental platform for fault identification

a)

b)

Fig. 13Photos of gear fault

a) Cracked planetary gear

b) Planetary gear with a missing tooth

The FIE-ASR method proposed in this paper can be used to process vibration signals, as shown in Fig. 14. Considering the rich spectra and complex sidebands of the response signals of planetary gearbox systems, the envelope spectrum of the original signal under each condition must be analyzed to avoid complex sideband analysis. First, for FIE, the characteristic frequency of the planet gear fault $f_p=$ 8 Hz is taken as the target frequency and the reference low frequency is set to $f_1=$ 0.004 Hz. To avoid spectrum leakage and the possibility of inaccurate characteristic frequency calculations, frequency information with a bandwidth of 0.05 Hz is exchanged while centered on $f_p$ or $f_1$. For example, the frequency bandwidth of 8 Hz±0.025 Hz exchanges information with 0.04 Hz±0.025 Hz.

Fig. 14Waveform, spectra, and envelope spectra of original vibration signals under different fault conditions: no fault (normal state), cracked gear, and a gear with a missing tooth

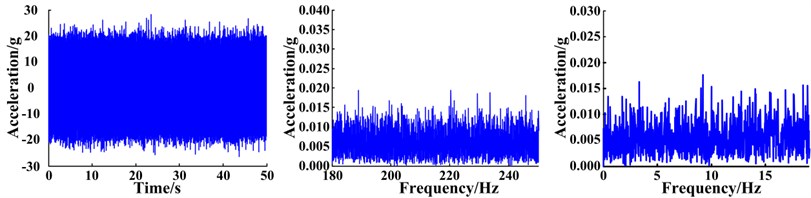
a) Normal state

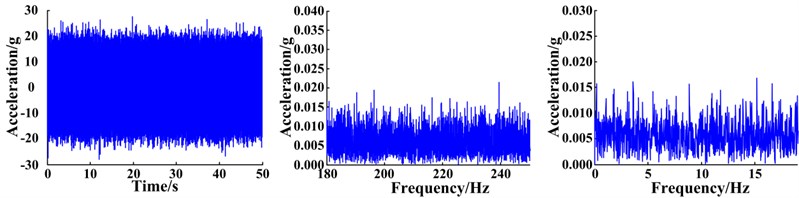
b) Planet gear crack

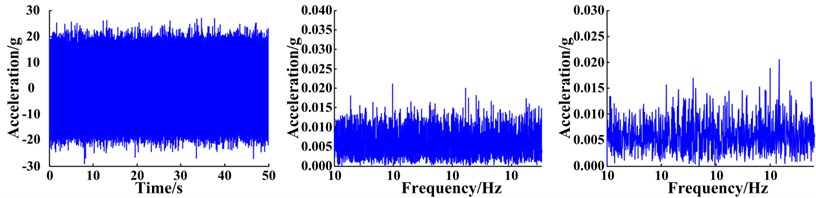
c) Planet gear with a tooth missing

After FIE, the resulting signals were subjected to inverse Fourier transformation to obtain the transformed envelope signal of each fault condition. The adaptive ant colony algorithm was used to optimize the parameters of the bi-stable system and the optimal parameters of each condition were substituted into the system. Then, the transformed envelope signal was input into the system to enhance the SR. The response waveforms and spectra are shown in Fig. 15.

Under normal conditions, no SR phenomenon occurs in the system response, suggesting the signal does not have a characteristic frequency component $f_p$ (Fig. 15). However, the SR phenomenon appears in the response of the systems with a cracked tooth and gear with missing tooth. From the response spectra, the amplitude at the reference frequency of $f_1=$ 0.04 Hz is particularly prominent and as the severity of the fault increases, the amplitudes of the signal become more evident. This is reflected by the fact that signals contain the characteristic frequency of the planetary gear fault corresponding to the reference frequency. The results are consistent with the real situation.

Fig. 15Waveforms and spectra of the bi-stable SR system responses for different gear faults based on the FIE-ASR method

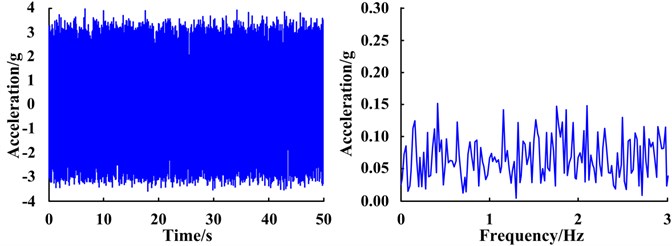
a) Normal state

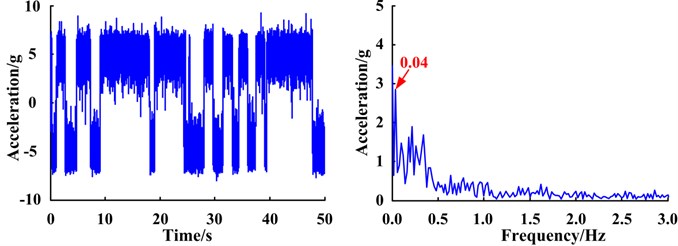
b) Planet gear crack

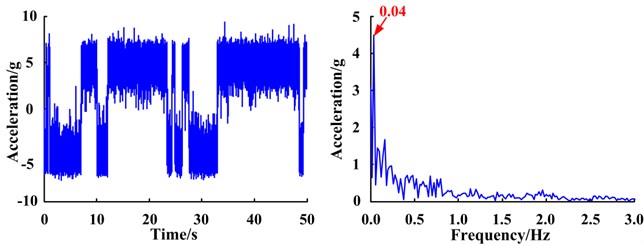
c) Planet gear with a missing tooth

4.2. Comparative analysis

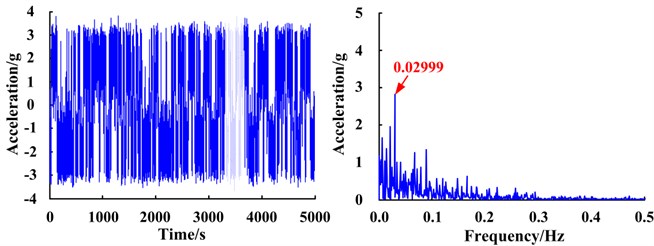
As a comparison, the traditional RF-ASR method was used on the same simulated test signals. Taking the missing tooth planet gear fault as an example, a scale factor $R=$ 100 Hz was selected, and each characteristic frequency was scaled to ${\stackrel{-}{f}}_c=$ 0.003 Hz or ${\stackrel{-}{f}}_p=$ 0.08 Hz. The scale-converted envelope signal and envelope spectra are shown in Fig. 16(a). The transformed envelope signal was input into the optimized bi-stable system to obtain the time-domain waveform and spectrum of the system response, as shown in Fig. 16(b).

The signal also undergoes the SR phenomenon (Fig. 16), however, based on the response spectra, it can be seen that the characteristic frequency corresponding to the enhanced frequency point is ${\stackrel{-}{f}}_c$ and not the fault characteristic frequency of the planet gear, and is therefore not the desired result, since it does not indicate whether a gear has failed. This phenomenon is caused by the Lorentz distribution of SR output Gaussian random noise [25]. Since harmonic components of a planetary gearbox are abundant, the characteristic frequency of the planetary carrier is much lower than the planetary gear fault (Table 1). Although the characteristic frequency satisfies the small-parameter conditions of SR after re-scaling the frequency, during the bi-stable SR enhancement process, Gaussian random noise energy converges to low frequencies. As the characteristic frequency decreases, it becomes much easier to enhance. Therefore, after the characteristic frequency of the planetary carrier is enhanced, the system transitions at this frequency, resulting in the SR phenomenon. Since the fault characteristic frequency of the planetary gear has not been enhanced, ultimately it cannot effectively detect planetary gear faults. The FIE-ASR method proposed in this paper overcomes this problem by dealing only with characteristic frequency bands of interest, thereby avoiding the influence of other harmonic components in the system. The above results demonstrate that the proposed method is more suitable than traditional RF-ASR methods for fault feature extraction of planetary gearbox systems with complex spectra.

Fig. 16Signal enhancement using re-scaling frequency-adaptive stochastic resonance (RF-ASR) method

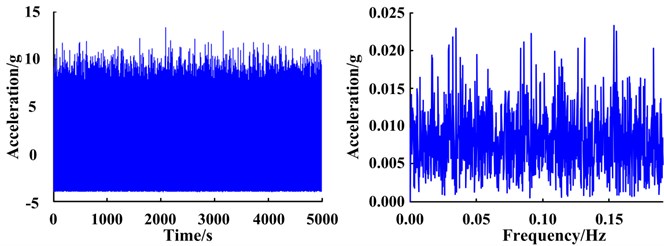
a) Scale-converted envelope signal and envelope spectrum

b) Waveform and spectrum of the system response