Modeling of stator system of asynchronous machine for magnetism and solid coupling vibration

1. Introduction

Electrical machines are one of the most fundamental motion generation mechanisms in industrial and agricultural products, even in the household electrical appliances in our daily life. Noise and vibration generate as well when the machines are working. Meanwhile, as a radiator of noise, the stator system plays an important role in the transmitting process of noise and vibration. Therefore, an accurate physical model of the stator system is essential for vibration analysis.

Researches show that the sound pressure lever and frame vibration are closely connected to both modal properties of the stator structure and frequency characteristics of the electromagnetic excitation forces [1, 2]. Thus, several physical models for the stator system are presented in previous works, such as single thin circular ring model, two concentric circular rings model, single thick cylindrical shell model [1], and two coaxial cylindrical shells named double-shell system here [3-5]. When the lengths of stator core and frame are the same, the modes are very close between double-shell model and two circular rings model in [3, 5]. Otherwise, the results are quite different.

Vibration and noise generated by an asynchronous machine can be reduced to a very large extent if the electromagnetic forces are not allowed to excite any kinds of resonances. For this reason, several analyses have been developed over the years. Ishibashi [6] studied the natural frequency and behavior of the stator by FEM, and the electromagnetic noise by boundary element method (BEM). Nahlaoui [7] presented an analytical method for fast estimation in the customizing process, and FEM for a more accurate result in the design process. On the other hand, electromagnetic forces of electric machines were analyzed by the method of Maxwell stress tensor for the vibrations in [8, 9].

The FEM for electromagnetic simulations can provide accurate solutions for the dynamic responses of an electrical machine with complicated stator and rotor shapes when the electrical machine is subjected to unbalanced magnetic forces. Meanwhile, the FEM is computationally expensive [10]. In the analytical method, the electromagnetic forces are determined by the currents, and introduced to the dynamic equations for resonance analysis. The electromagnetic behaviors have an influence on the mechanical behaviors, and the influence of the mechanical behaviors on the electromagnetic behaviors is neglected. However, in the real electrical machine, there is a mutual interaction between the electromagnetic and mechanical behaviors. Therefore, this mutual interaction must be studied in the dynamic analysis of electrical machine.

In this work, the dynamic behaviors of the stator system of the asynchronous machine are investigated when the electromagnetic and mechanical interaction is considered. Based on the improved physical model of the stator system, introducing the electromagnetic force with the stator radial displacement to the dynamic equation of the stator system, primary parametric vibration are analyzed by the method of multiple scales. Moreover, the effects of electromagnetic and mechanical parameters on resonance characteristics are analyzed.

2. Improved physical model

In this paper, a three-phase asynchronous machine is considered as a principle prototype, and its stator system is composed of stator core and frame interconnected by key bars. The stator core is considered as inner shell, and the frame is considered as outer shell of double-shell system. Especially, the length of the core is much shorter than that of the frame. Thus, the physical model is established as Fig. 1.

Fig. 1Double-shell system with unequal lengths

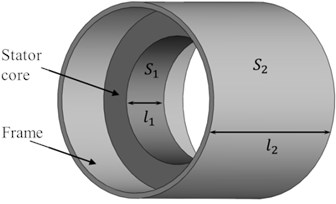
a)

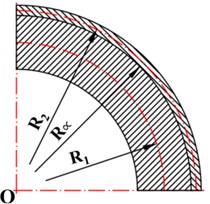
b)

For a single thin shell, the displacement variational principle can be easily obtained by the Hamilton’s Principle. However, attention should be paid to the connection condition between two shells. Based on these conditions, using the method presented in [11], the vibration equation with modal damping can be obtained as:

where $R_{\beta }$ is the centroid radius of the stator core. The superscript $s$ is for the stator, $r$ is for the frame, and the subscript $i$ represents the orders of natural frequencies. $M_i$ is the mass matrix. The displacement solutions can be written as the products of periodic function $T_i\left(t\right)$ and the radial mode shape function $W_{is}$ corresponding to natural frequencies based on [12]. ${\mu }_i$ is damping coefficient, and the frequency of double-shell system is obtained as:

where ${\omega }_{is}$ and ${\omega }_{ir}$ are the frequencies of the stator core and the frame, respectively. Here, the frequencies of the complex stator structure can be calculated by this simple way. It is convenient to analyze vibration mechanism of the stator system based on this analytical model.

3. Model verification

Eq. (2) is the expression of natural frequencies of double-shell system. Here, EMA and FEM are used to verify the method. Fig. 2 is the comparison of mode shapes obtained by EMA and FEM. With modal identification and numerical calculation, the calculation results of natural frequencies obtained by the analytical method (method 1), the EMA (method 2) and the FEM (method 3), are shown in Fig. 3. The margin of error between analytical solution and EMA on the first frequency is only 2.89 %, and the deviation of all results is no more than 5 %. Therefore, it can be concluded that the analytical method provides a very good match. And the double-shell stator system with unequal length can be used for further study on vibration mechanism.

Fig. 2Comparison of mode shapes

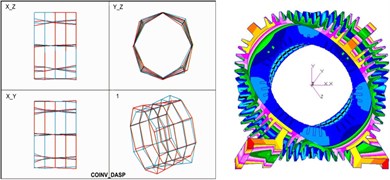
a) First-order (332.467 Hz)

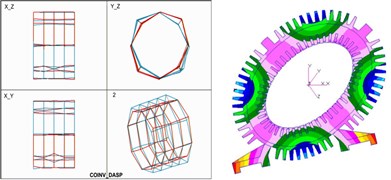
b) Second-order (522.303 Hz)

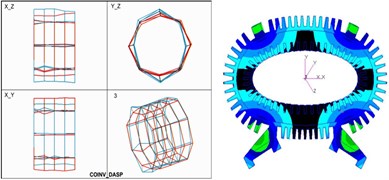
c) Third-order (580.433 Hz)

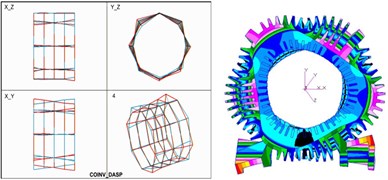
d) Fourth-order (822.653 Hz)

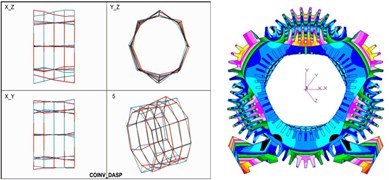
e) Fifth-order (950.473 Hz)

Fig. 3Comparison of natural frequencies

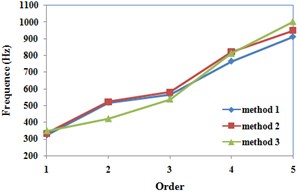
Fig. 4Comparison of models

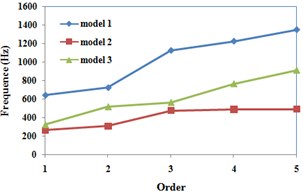
To show the precision, Fig. 4 is the comparison of three models based on [3, 5]. Both model 1 and 2 are with equal length between the stator core and the frame. The length of the stator core is stretched along the length of the frame in model 1. On the contrary, the length of the frame is compressed to the length of the stator core in model 2. The comparison indicates that the model 1 and 2 with equal length cannot represent the natural characteristics of double-shell stator system. The difference between the stator core and the frame makes the natural frequencies change a lot. The model 3 presented in this paper can take the difference in consideration.

In conclusion, by the comparison of different methods and different models, the new double-shell model can be used in a wider application range. Using this model, the vibration modes can be described by the analytical expression, and different boundary conditions between the stator core and the frame can be respectively considered. Meanwhile, the natural characteristics of the double-shell stator system with different length rates can be calculated.

4. Improved electromagnetic force

The radial electromagnetic forces that act on the stator core are evaluated by Maxwell stress based on [7, 8]:

where $B$ is the air-gap flux density, and ${\mu }_0$ is the vacuum magnetic permeability. It is generally commonly accepted that the tangential component is negligible in the analysis of radial vibration, as done in [13]. $\mathrm{\Lambda }$ is air-gap magnetic performance, and $f$ is the magnetomotive force synthesized by windings, and includes fundamental component, harmonic components of stator windings and rotor windings. The air-gap magnetic performance can be improved as:

where ${\mathrm{\Lambda }}_0$ is the average air-gap magnetic permeance, $W=w_s/{\delta }_0$ is the dimensionless radial displacement of the stator core, and ${\delta }_0$ is the average eccentricity.

Therefore, the expression of electromagnetic force can be derived as:

where $Z_0$, $Z_1$ and $Z_2$ are the coefficients of each component of electromagnetic force, and they are determined by the magnetomotive force $f$. ${\mathrm{\Omega }}_n={\omega }_1\pm {\omega }_{\mu }$ are the frequencies of electromagnetic force corresponding to $\gamma =\nu \pm \mu$. The phase angles are neglected in vibration analysis, as done in [5].

5. Magnetism and solid coupling primary parametric resonance

The vibration equation by the action of electromagnetic force has been obtained in Eq. (1). Substituting Eq. (5) into Eq. (1), the partial differential vibration equations of dynamic system with the interaction between electromagnetic and mechanical field are obtained when the order $i$ of natural frequency is equal to $\gamma$:

where ${\stackrel{-}{\omega }}_{\gamma }^2={\omega }_{\gamma }^2-\frac{R_{\beta }}{M_{\gamma s}+M_{\gamma r}}\underset{s_1}{\iint }{Z}_1{w}_s{W}_{\gamma s}\mathrm{d}x\mathrm{d}\theta$, it is the resonance frequency of the stator system. $\mathrm{\Gamma }$ are the coupling coefficients, which present the coupling of different mode shapes. And ${\eta }_{rn}$ are the coefficients from $Z_n$. The subscripts $j$, $k$ and $l$ represent the orders of mode shapes, same as $i$.

Eq. (6) shows that the vibration equation is effected by the electromagnetic and mechanical parameters. The method of multiple scales is introduced to analyze the coupling resonance. In the case of ${\mathrm{\Omega }}_n\approx {\stackrel{-}{\omega }}_{\gamma }$, the stator system is on primary parametric resonance. We express the nearness of ${\mathrm{\Omega }}_n$ to ${\stackrel{-}{\omega }}_{\gamma }$ by introducing the detuning parameter $\delta$ according to:

For steady-state solution, the amplitude-frequency equation can be obtained:

where $k$ is the proportional coefficient of excitation amplitude.

6. Qualitative analysis

Eq. (8) shows that the amplitude is connected to the electromagnetic force $F_{\gamma }$, electromagnetic parameters ${\eta }_{\gamma n}$, damping parameter ${\mu }_{\gamma }$, and the frequency detuning parameter $\epsilon \delta$. When the coupling coefficient $\mathrm{\Gamma }$ is zero, the resonance will not be excited. Solid line represents stable solution, and dashed line represents unstable solution in Fig. 5 and Fig. 6.

Fig. 5 is the curves that the resonance amplitude varies with excitation amplitude and damping parameter. In the case of $F=0$, the resonance curves indicate that the double-shell system is excited to parametrical resonance in Fig. 5(a), and in the case of strong excitation, the resonance curves show the forced vibration characteristic in Fig. 5(b). The curves both in Fig. 5(a) and Fig. 5(b) present toward right deviation and express the hard characteristic, and the resonance region decreases with the damping parameter increasing in Fig. 5(a). Fig. 5(c) is the curves that the amplitude varies with the proportional coefficient of excitation amplitude. There is no jump phenomenon when $\mu =0$. With the damping increasing, the resonance region is decreasing, and there are jump points when $\mu =0.6$ and $\mu =1$. That means when $k$ is less than the jump point, the parametrical vibration is the main role, and the forced vibration is the leading role when $k$ is more than the jump point.

Fig. 5Amplitude-excitation amplitude curves

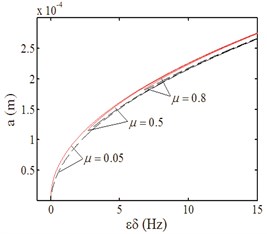
a)

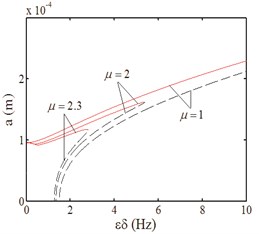
b)

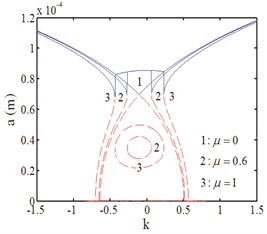
c)

Fig. 6Amplitude-magnetic density curves

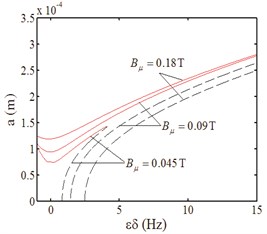
a)

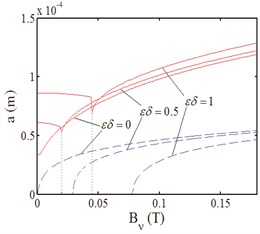
b)

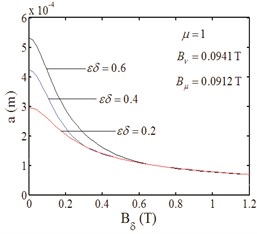
c)

Fig. 6 indicates the effect of electromagnetic parameters and detuning parameter on resonance response. In Fig. 6, $B(B{}_{\delta }{}^{\mathrm{}}\mathrm{},B_{\nu },B_{\mu })={\mathrm{\Lambda }}_0\cdot F(F_{\delta },F_{\nu },F_{\mu })$. The resonance region is broadening with both the harmonic magnetic flux density of rotor and stator increasing in Fig. 6(a) and Fig. 6(b). When the harmonic flux density of the stator is small, its effect on the amplitude is weak. After the certain value, the effect becomes strong in Fig. 6(b). However, the fundamental component $B_{\delta }$ is a damping to the resonance in Fig. 6(c). And with the detuning parameter increasing, the effect becomes strong. Furthermore, the effect becomes weaker as the air-gap magnetic flux density increasing.

7. Conclusion

The improved model with unequal length between the stator core and the frame is established to study the magnetism and solid coupling vibration of the stator system as the radiator of electromagnetic noise. The results of EMA and FEM are given to verify the methodology. This double-shell model can be used to calculate the natural characteristics of the stator system with different length rates. And it can make different boundary conditions between the stator core and the frame in consideration. Furthermore, it will be used to solve the coupling vibration of stator and rotor.

The improved electromagnetic force expression reflects the interaction between electromagnetic and mechanical behaviors. This force can excite primary parametric vibration, double resonances, and the multiple resonances. These resonances are the sources of electromagnetic noise. Moreover, they can lead the asynchronous machine to accidents.

The modeling and the study on magnetism and solid coupling vibration excited by electromagnetic force lay a foundation for the design of electric machines.