The study on magnetism and solid coupling vibration and its electromagnetic force characteristics in stator system of electrical machine

1. Introduction

With the development of research, electromagnetic noise has become the main noise source of large and medium sized electrical machines. As the electromagnetic vibration of the electrical machines originated from the coupling between the electromagnetic field and mechanical motion, the study on its magnetism and solid coupling vibration mechanism is a necessary path for the vibration and noise reduction. And the stator system is not the only one of noise sources, but also as a conduction medium of the other noise sources. Therefore, it is very important to study the magnetism and solid coupling vibration of the stator system in electrical machines.

The electromagnetic noise is produced by the interaction between stator core motion and electromagnetic force. This interaction is reflected in two aspects. One is the interaction between air gap magnetic field and the cores of stator and rotor, which named air gap magnetic pull, an external force. The other is electromagnetic volume force generated by electromagnetic field inside the core, which is named ponderomotive force, an internal force. This volume force contains Lorenz force and magnetostrictive force. By the alternating electromagnetic forces, the stator and rotor will be excited strong nonlinear vibration.

Many researches have been developed in electromagnetic vibration excited by the unbalance magnetic force (UMP) between the stator and rotor surfaces. The approximate analytical method and numerical method are used frequently. Donát M. noticed the influence of rotor eccentricity on the vibration and noise, and calculated the electromagnetic force and its dynamic response in asynchronous generator [1]. Besnerais J. Le gave qualitative analysis of the cause of electromagnetic force waves in asynchronous machine [2]. Many researchers analyzed the electromagnetic vibration based on the 2D electromagnetic field and 3D structure finite element model [3, 4].

However, some of the researchers had found that the origins of electromagnetic excitation which are the Maxwell forces, the Lorentz forces and the magnetostrictrive forces [5, 6]. But the accurate analytical expression is not presented by now. The stator core, as a conductive medium, will generate the electromagnetic force under the reaction of electromagnetic field. In addition, the numerical method is used to describe electromagnetic field distribution. It’s very inconvenience to the analysis of electro-magnetic and solid coupling vibration. Therefore, by the analytical method, the analytical expressions of electromagnetic field and forces can be derived for further nonlinear vibration analysis, and the computation time can be greatly reduced.

In this work, by the analysis of electromagnetic forces, the magnetism and solid coupling vibration equation with both the air gap magnetic pull and the ponderomotive force is given based on the double-shell stator system. For the analysis of electromagnetic field and force in the stator core, according to the Maxwell equations, the eddy equations are obtained and solved for the study on variation law of the geometric parameters, current density, magnetic flux density and electromagnetic forces. Then the magnetism and solid coupling vibration differential equation is improved. And the methodology of electromagnetic design of motor stator system is enriched.

2. Electromagnetic force of stator system

The electromagnetic force for the stator system contains normal and tangential electromagnetic forces ($f_n$ and $f_t$) per unit area on inner surface of the stator respectively, and electromagnetic volume force $f_T$ generated by eddy current inside the stator core. The $f_n$ and $f_t$ are the radial and tangential components of the air gap magnetic pull, and they are external forces. On the interface between two different mediums, these two forces can be expressed as:

where $B_{1n}$, $B_{2n}$, $B_{1t}$ and $B_{2t}$ are normal and tangential components of magnetic flux densities on the surfaces of two mediums, respectively. ${\mu }_1$ and ${\mu }_2$ are the magnetic permeabilities, respectively.

On the other hand, the electromagnetic volume force can be expressed as:

where ${\mathbf{f}}_1$ is Lorenz force. When the magnetic medium is linear and uniform, grad $\mu =$0 in the magnetic medium. ${\mathbf{f}}_3$ is magnetostrictive force. It has no effect on total force and torque of the whole magnetic medium. And it doesn’t change with the deformation of magnetic medium. Therefore, it can be ignored. Then, the electromagnetic volume force can be simplified as:

where, $\mathbf{J}$ is current density vector, and $\mathbf{B}$ is magnetic flux density vector.

3. Improved magnetism and solid coupling vibration differential equation

The double-shell stator structure is shown in Fig. 1. The electromagnetic volume force generated by eddy current in the stator core can be projected in three directions as:

where $x$, $\theta$, $r$ are cylindrical coordinates, respectively. Electromagnetic field only exists in the core, therefore Eq. (4) can be simplified on the middle surface of the stator shell as.

Principal vector:

Principal moment:

According to the author's previous work [7], the magnetism and solid coupling vibration differential equation with modal damping can be improved as:

where $c_i$ is modal damping coefficient, and ${\omega }_i$ is the natural frequency of double-shell system. The first term at the right end of the equal sign reflects the effect of the ponderomotive force (Lorentz force) produced by the electromagnetic field inside the stator core. And the second term reflects the effect of the electromagnetic force (air gap magnetic pull) on the stator core.

Fig. 1Double-shell stator system

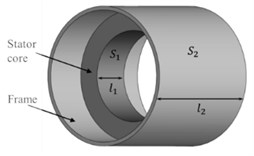
4. The solution of electro-magnetic field inside the stator core

Based on the Maxwell equations and electromagnetic constitutive relation, according to the three-phase asynchronous machine structure, the 2D electromagnetic field is studied for qualitative analysis. Introducing a vector magnetic potential $\mathbf{A}$, the electromagnetic field equations can be expressed as:

where $\mathbf{E}$ is electric field intensity vector, $\sigma$ is conductivity, furthermore, ${\mu }_r={\mu }_0={\mu }_x=\mu$, ${\sigma }_r={\sigma }_{\theta }$, and ${\sigma }_x=\sigma \ll {\sigma }_r$.

Through simplification and deduction of equations, the expressions of magnetic flux density and eddy current density inside the stator core are:

And the electromagnetic force produced by the eddy current inside the stator core can be expressed as:

Therefore, if the expression of magnetic potential can be obtained, the electromagnetic field and force in the stator core can be determined. Considering the 2D magnetic field problem, the vector magnetic potential $\mathbf{A}$ can be simplified as:

Substituting Eq. (9) into the third equation of Eqs. (6), the eddy equation can be derived as:

Solving this Helmholtz equation by the method of separation of variables, the magnetic potential $A_x$ can be obtained based on the boundary conditions. And furthermore, substituting it into Eq. (7) and Eq. (8), the magnetic flux density, eddy current density and electro-magnetic forces can all be solved.

5. Numerical simulation and discussion

Take a three-phase asynchronous machine as an example to discuss the influence of geometric parameters on electromagnetic field and forces.

Fig. 2 shows that the magnetic flux density $B_r$ and $B_{\theta }$, eddy current density $J_x$, and electro-magnetic forces $f_r$ and $f_{\theta }$($f_r/\sigma$ and $f_{\theta }/\sigma$ in the Fig. 2) curves with the radius. And the time can be taken as $t=2n\pi$ ($n=$1, 2, 3...). The figures present the variation of curves in one period with different angles. The radial components of the magnetic flux density, the eddy current density and the circumferential electromagnetic force are zero at the outer diameter of the stator core. But the circumferential magnetic flux density is zero at the inner diameter. The radial component of the electromagnetic force is zero both at the inner and outer diameter, and its maximum appears inside the stator core.

Fig. 2Magnetic flux density, current density and electromagnetic force-radius curves

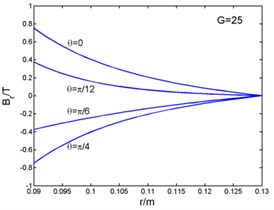
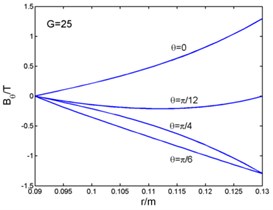
a)$B_r~r$

b)$B_{\theta }~r$

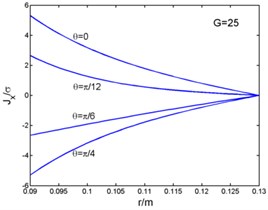
c)$J_x/\sigma ~r$

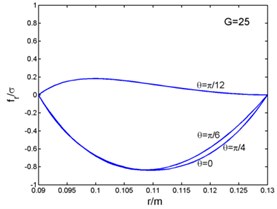
d)$f_r/\sigma ~r$

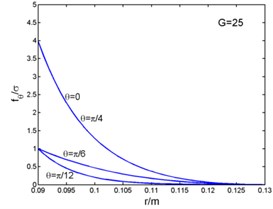
e)$f_{\theta }/\sigma ~r$

Fig. 3 shows that the magnetic flux density $B_r$ and $B_{\theta }$, eddy current density $J_x\text{,}$ and electro-magnetic forces $f_r$ and $f_{\theta }$($f_r/\sigma$ and $f_{\theta }/\sigma$ in the Fig. 3) curves with the changing of angle. And the angle can be taken as $t=2n\pi$ ($n=$1, 2, 3...). The figures illustrate the variation of physical quantities in one circumferential range with different radii. The radial and circumferential components of the magnetic flux density and the eddy current density are in the form of four times harmonic harmonics in a period. But the electromagnetic volume forces are in the form of eight times harmonic harmonics in a period. When this frequency is related to the natural frequency of the stator system, and meets the modal coupling relationship, the stator system will excite principal parametric resonance, subharmonic resonance and superharmonic resonance, and so on.

Fig. 3Magnetic flux density, current density and electromagnetic force – angle curves

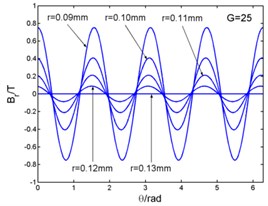
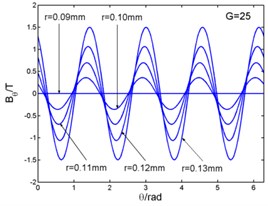
a)$B_r~\theta$

b)$B_{\theta }~\theta$

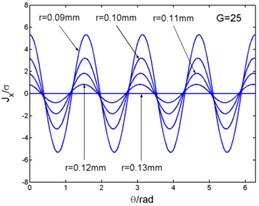
c)$J_x/\sigma ~\theta$

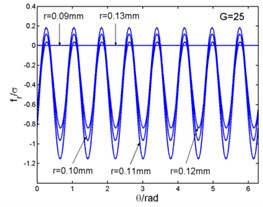
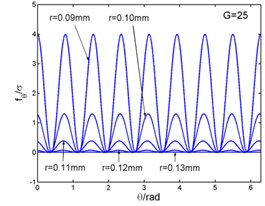
d)$f_r/\sigma ~\theta$

e)$f_{\theta }/\sigma ~\theta$

6. Conclusions

The magnetism and solid coupling vibration differential equation is derived and improved by the analysis of the ponderomotive force produced by eddy inside the stator core. Through the derivation, the electromagnetic field and forces can be obtained by the introducing of the magnetic potential. It is proved that the magnetism and solid coupling vibration of the stator system is generated by the interaction between the external air gap magnetic field and the internal magnetic field of the stator core.

The qualitative analysis of electromagnetic field and force illustrate the variation law of physical quantities and frequency relation. The method presented in this paper can be extended to the case where the high-order harmonic magnetic potential of stator and rotor windings is taken into account. The work in this paper also lays a foundation for the analysis of the magnetism and solid coupling vibration mechanism between the stator and rotor.