Analysis of electromagnetic characteristic in the interior permanent magnet brushless DC motor

Li, Zhengyang; Wan, Yi; Xia, Yan; Gong, Fangbin; Wang, Qiang; Chen, Fei

doi:10.21595/mme.2022.22950

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 30 September 2022

Check for updates

Analysis of electromagnetic characteristic in the interior permanent magnet brushless DC motor

Zhengyang Li¹

Yi Wan²

Yan Xia³

Fangbin Gong⁴

Qiang Wang⁵

Fei Chen⁶

^{1, 2}Key Laboratory of High Efficiency and Clean Mechanical Manufacture, Ministry of Education, School of Mechanical Engineering, Shandong University, Jinan, China

^{1, 2}National Demonstration Center for Experimental Mechanical Engineering Education, Shandong University, Jinan, China

³School of Mechanical Engineering, Qilu University of Technology (Shandong Academy of Sciences), Jinan, China

^{4, 5, 6}DeZhou HengLi Electrical Machinery Co., Ltd, Dezhou, China

Corresponding Author:

Yi Wan

Cite the article Download PDF

Downloads 437

Abstract

The motor vibration is mainly induced by the electromagnetic excitation. In order to improve the running performance of the permanent magnet brushless DC motor (BLDCM) within the rolling rotor compressor, this paper builds the predicted model of the electromagnetic excitation and analyzes the electromagnetic characteristic of the BLDCM. Firstly, the electromagnetic field is divided into four regions in 2D plane, including the magnet, air gap, stator slot, and slot-opening subdomains. Then, the relative equations of the electromagnetic field are constructed, and the vector magnetic potential is solved by the variable separation method. Thus, the magnetic flux density of the air gap is derived by the corresponding vector magnetic potential, which is used to describe the electromagnetic excitation. Based on the built model, the effects of the slot opening and air gap length on the electromagnetic characteristic are analyzed. The analysis results can provide a reference for the improvement of the electromagnetic characteristic of the BLDCM by structure optimization.

Analysis of electromagnetic characteristic in the interior permanent magnet brushless DC motor

Highlights

A 3D model of BLDCM is built to analyze its sturcture.
The electromagnetic characteristic of the BLDCM was analyzed.
The effect of the slot opening on the magnetic flux density was analyzed.
The effect of the air gap length on the electromagnetic force was analyzed.

1. Introduction

Due to the traits of high efficiency, easy control, long-life, simple construction and so on, the BLDCM is widely used in the various fields, especially in the home appliance [1]. For example, the BLDCM within the rolling rotor compressor is selected as the driving motor in the air conditioning. The vibration of the BLDCM could directly affect the running performance of the overall system, which is mainly caused by the electromagnetic excitation [2].

The research methods for the motor electromagnetic fields mainly include the analytical method, the finite element method (FEM), the graphical method, and so on. The FEM can ensure the predicted accuracy, but it will loss the efficiency. The analytical method shows the good calculated efficiency. Such as, Zhu et al. [3] investigated the effect of stator slotting on the radial magnetic field distribution. Dubas et al. [4] developed a new analytical solution for the multipole surface mounted permanent-magnet motors, where both the radial and parallel magnetization and the slotting effect were considered. Then, Zhu et al. [5] built an accurate analytical subdomain model for the magnetic field computation in surface-mounted permanent-magnet machines. Additionally, Lubin et al. [6] also proposed an analytical subdomain model to compute the magnetic field distribution in surface-mounted permanent-magnet motors with semi-closed slots, where the expression and solution of this model show more simplified and simple. He et al. [7] investigated the influence of rotor eccentricity on the electromagnetic performance by the finite element analyses and experiments.

In this paper, in order to investigate the electromagnetic characteristic of the BLDCM, the method [6] is introduced to describe the electromagnetic field. In Section 2, the predicted model is constructed by combining the equations of the different subdomains in 2D polar coordinates, and thus the electromagnetic excitation is derived and obtained. Then, the effects of the structure parameter including the slot opening and air gap length on the electromagnetic characteristic are analyzed in Section 3. Finally, some conclusions are listed in Section 4.

2. Analytical model of magnetic field of the BLDCM

2.1. Physical model of BLDCM

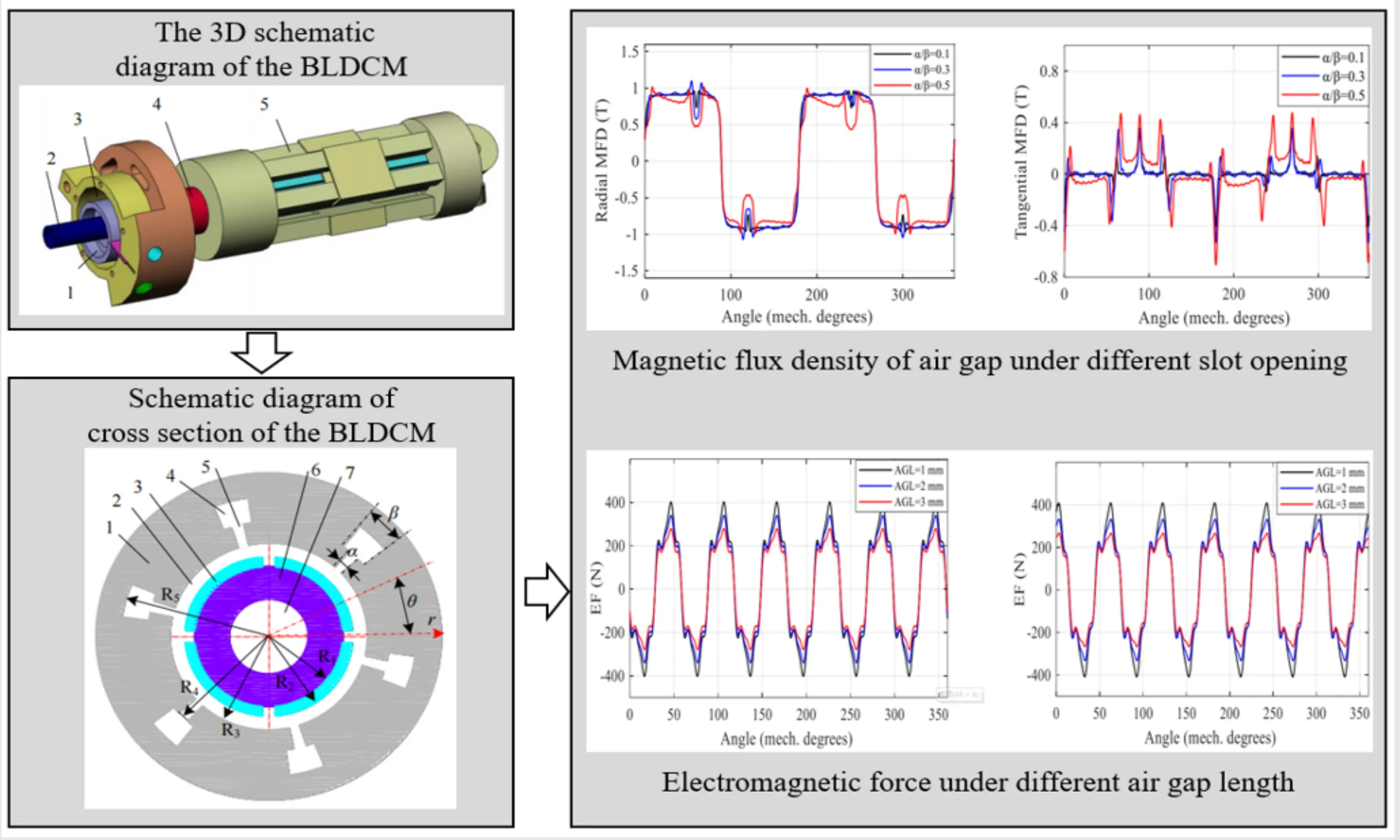
The BLDCM in this paper is inside the rolling rotor compressor used in the refrigeration equipment, such as air conditioning, refrigerators, and so on. The motor mainly consists of the rotor, stator, rolling rotor, shaft, sliding bearing and shell, whose 3D structure is shown in Fig. 1. The rotor, rolling rotor and sliding bearing are mounted on the same rotating shaft. During running, the BLDCM drives the rotating shaft and rolling rotor to rotate, which changes the volume of the working cavity composed of the rolling rotor and air cylinder to compress gas. As the basis of analysis the dynamic characteristic of the BLDCM, the electromagnetic excitation is investigated in the next subsection.

Fig. 1The 3D schematic diagram of the BLDCM: 1 – rolling rotor; 2 –shaft; 3 – air cylinder; 4 – upper bearing; 5 – stator

2.2. Analytical model of magnetic field

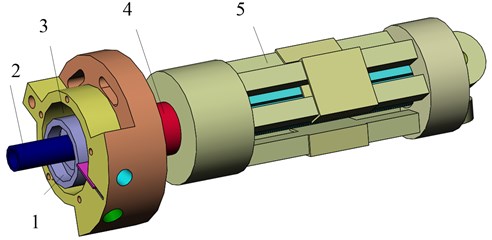
In Fig. 2, the cross section of the BLDCM is artificially divided into four parts, including the magnet, air gap, stator slot, and slot-opening subdomains. In 2D polar coordinates, i.e. $(r, θ)$ , $R_{1}$ and $R_{2}$ are the inner and outer radiuses of the permanent magnet, respectively. The rotor and permanent magnet subdomain are in contact at $R_{1}$ ; the two subdomains of the permanent magnet and air gap are in contact at $R_{2}$ . And $R_{3}$ are the outer radius of the air gap subdomain, where the two subdomains of the air gap and slot-opening are in contact at $R_{3}$ . $R_{4}$ and $R_{5}$ are the outer radiuses of the slot-opening and stator slot subdomains, respectively. In addition, $α$ and $β$ are the slot-opening angle and the slot-pitch angle, respectively.

For the sake of convenient analysis, some assumptions are listed as follows: (1) the silicon steel sheets are infinitely permeable; (2) the end effect is ignored; (3) the relative permeability of permanent magnet subdomain $μ_{0} \neq 1$ .

In air-gap subdomain, the Laplace equation can be built in forms of polar coordinates, which can be described as:

1

\frac{\partial^{2} A_{2}}{\partial r^{2}} + \frac{1}{r} \frac{\partial A_{2}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} A_{2}}{\partial θ^{2}} = 0, R_{2} \leq r \leq R_{3}, 0 \leq θ \leq 2 π,

where $A_{2}$ is the vector magnetic potential of air gap subdomain.

The boundary conditions of the air gap subdomain are:

2

\begin{array}{l} {\frac{\partial A_{2}}{\partial r}|}_{r = R_{2}} = {\frac{1}{μ_{0}} \frac{\partial A_{1}}{\partial r}|}_{r = R_{2}}, \\ {\frac{\partial A_{2}}{\partial r}|}_{r = R_{3}} = \{\begin{array}{l} {\frac{\partial A_{3}}{\partial r}|}_{r = R_{3}}, & θ - \frac{α}{2} \leq θ \leq θ + \frac{α}{2}, \\ 0, & o t h e r s, \end{array} \end{array}

where $A_{1}$ and $A_{3}$ are the vector magnetic potentials of the permanent magnet and slot-opening subdomains, respectively.

Fig. 2Schematic diagram of cross section of the BLDCM: 1 – stator; 2 – air gap; 3 – permanent magnet; 4 – slot; 5 – slot opening; 6 – rotor; 7 – shaft

Based on the variable separation method, Eq. (1) can be solved, whose general solution can be expressed by:

3

\begin{array}{l} A_{2} = \sum_{n = 1}^{\infty} [E_{n} \frac{R_{2}}{n} \frac{S_{n} (r, R_{3})}{T_{n} (R_{2}, R_{3})} + F_{n} \frac{R_{3}}{n} \frac{S_{n} (r, R_{2})}{T_{n} (R_{3}, R_{2})}] c o s (n θ) \\ + \sum_{n = 1}^{\infty} [G_{n} \frac{R_{2}}{n} \frac{S_{n} (r, R_{3})}{T_{n} (R_{2}, R_{3})} + H_{n} \frac{R_{3}}{n} \frac{S_{n} (r, R_{2})}{T_{n} (R_{3}, R_{2})}] s i n (n θ), \end{array}

where $E_{n}$ , $F_{n}$ , $G_{n}$ and $H_{n}$ refer to the harmonic coefficients of the magnetic vector potential in the air gap. Functions $S$ and $T$ are used to deal with the solutions of the magnetic vector potential [6].

The relationship between the magnetic flux density and the vector magnetic potential can be described as:

4

B_{r} = \frac{1}{r} \frac{\partial A}{\partial θ} B_{θ} = - \frac{\partial A}{\partial θ} .

Based on the Eq. (4), the radial and tangential magnetic flux density in the air gap can be obtained by:

5

\begin{matrix} B_{2 r} = \sum_{n = 1}^{\infty} [P_{1 n} s i n (n θ) + P_{3 n} c o s (n θ)], B_{2 θ} = \sum_{n = 1}^{\infty} [P_{2 n} s i n (n θ) + P_{4 n} c o s (n θ)], \end{matrix}

where:

6

\begin{array}{l} P_{1 n} = - \frac{1}{r} [E_{n} R_{2} \frac{S_{n} (r, R_{3})}{T_{n} (R_{2}, R_{3})} + F_{n} R_{3} \frac{S_{n} (r, R_{2})}{T_{n} (R_{3}, R_{2})}], \\ P_{2 n} = - \frac{1}{r} [G_{n} R_{2} \frac{T_{n} (r, R_{3})}{T_{n} (R_{2}, R_{3})} + H_{n} R_{3} \frac{T_{n} (r, R_{2})}{T_{n} (R_{3}, R_{2})}], \\ P_{3 n} = \frac{1}{r} [G_{n} R_{2} \frac{S_{n} (r, R_{3})}{T_{n} (R_{2}, R_{3})} + H_{n} R_{3} \frac{S_{n} (r, R_{2})}{T_{n} (R_{3}, R_{2})}], \\ P_{4 n} = - \frac{1}{r} [E_{n} R_{2} \frac{T_{n} (r, R_{3})}{T_{n} (R_{2}, R_{3})} + F_{n} R_{3} \frac{T_{n} (r, R_{2})}{T_{n} (R_{3}, R_{2})}], \end{array}

where $n$ is a positive integer.

The electromagnetic torque can be expressed by:

7

T_{e} = \frac{L_{m} r^{2}}{μ_{0}} \int_{0}^{2 π} B_{2 r} (r, θ) B_{2 θ} (r, θ) d θ, R_{2} < r < R_{3},

where $L_{m}$ is the axial length of the stator core, and $μ_{0}$ is the air gap permeability.

Substitution Eq. (5) into Eq. (7), the electromagnetic torque can be described by the Fourier series:

8

T_{e} = \frac{π L_{m} r^{2}}{μ_{0}} \sum_{n = 1}^{\infty} (P_{1 n} P_{2 n} P_{3 n} P_{4 n}) .

Based on the Maxwell tensor formula, the electromagnetic force along $x$ and $y$ directions can be written as:

9

\begin{array}{l} F_{e x} = \frac{L_{m} r}{2 μ_{0}} \int_{0}^{2 π} [(B_{2 r}^{2} - B_{2 θ}^{2}) c o s θ - 2 B_{2 r} B_{2 θ} s i n θ] d θ, \\ F_{e y} = \frac{L_{m} r}{2 μ_{0}} \int_{0}^{2 π} [(B_{2 r}^{2} - B_{2 θ}^{2}) s i n θ + 2 B_{2 r} B_{2 θ} c o s θ] d θ . \end{array}

Then, substituting the magnetic flux density in Eq. (5) into Eq. (9), Eq. (9) can be rewritten as the follows:

10

\begin{array}{l} F_{e x} = \frac{π L_{m} r}{4 μ_{0}} \sum_{|j - n| = 1} (P_{1 j} P_{1 n} - P_{2 j} P_{2 n} + P_{3 j} P_{3 n} - P_{4 j} P_{4 n}) \\ - \frac{π L_{m} r}{2 μ_{0}} [\sum_{j - n = 1} (P_{1 j} P_{2 n} - P_{3 j} P_{4 n}) - \sum_{j - n = - 1} (P_{1 j} P_{2 n} - P_{3 j} P_{4 n})], \\ F_{e y} = \frac{π L_{m} r}{4 μ_{0}} \sum_{j - n = 1} (P_{1 j} P_{3 n} - P_{3 j} P_{1 n} - P_{2 j} P_{4 n} + P_{4 j} P_{2 n}) \\ - \frac{π L_{m} r}{4 μ_{0}} \sum_{j - n = - 1} (P_{1 j} P_{3 n} - P_{3 j} P_{1 n} - P_{2 j} P_{4 n} + P_{4 j} P_{2 n}) + \frac{π L_{m} r}{2 μ_{0}} \sum_{|j - n| = 1} (P_{1 j} P_{2 n} + P_{3 j} P_{4 n}) . \end{array}

3. Analysis of electromagnetic characteristic of the BLDCM

This paper takes the BLDCM in the rolling rotor compressor of an air conditioner as an example, where the corresponding system parameters are listed in Table 1. Then, the system parameters are substituted into the above equations to obtain the electromagnetic excitation. The effects of the air gap length and the slot opening on the electromagnetic characteristic are analyzed in detail.

Table 1Parameters of the BLDCM

Items	Value	Items	Value
Axial length of stator $L_{m}$	80 (mm)	Pole-arc coefficient	1
Outer radius of rotor $R_{1}$	24.6 (mm)	Pole-pairs number	2
Outer radius of magnet $R_{2}$	27.7 (mm)	Number of stator slots	6
Radius of stator bore $R_{3}$	28.9(mm)	Relative permeability of magnet $μ_{0}$	1.02
Radius of slot opening $R_{4}$	31 (mm)	Residual magnetic flux density $B_{r}$	1.2 T
Radius of slot $R_{5}$	46.4 (mm)	Speed of motor	3000 r/min

3.1. The effect of the slot opening on the magnetic flux density (MFD)

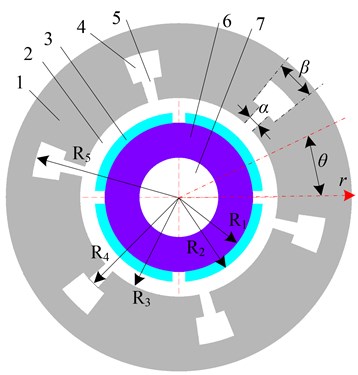
In order to analyze the effect of the slot opening ( $α$ / $β$ ) on the magnetic flux density (MFD), three values of the slot opening are selected, including $α$ / $β$ = 0.1, 0.3 and 0.5. The radial and tangential MFDs of the air gap are illustrated in the Fig. 3. In the figure, when the slot opening increases from 0.1 to 0.5, the fluctuation of magnetic flux density gradually aggravates. Especially, the radial MFDs obviously fluctuate at the slot opening. This shows that the fluctuation resulted from slot opening directly affects the electromagnetic excitation.

Fig. 3Magnetic flux density of air gap under different slot opening

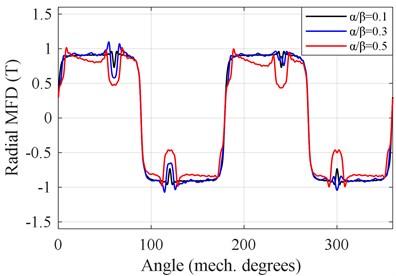
a) Radial MFD

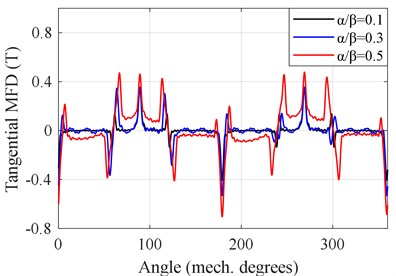
b) Tangential MFD

3.2. The effect of the air gap length on the electromagnetic force

Under the different air gap length, the rotor is subjected to the different electromagnetic forces, which further affects the dynamic characteristic of the motor. The air gap length (AGL) is selected with 1 mm, 2 mm and 3 mm, where the slot opening is 0.1. Then, the obtained electromagnetic forces (EFs) along $x$ and $y$ directions are shown in Fig. 4. When the air gap length increases, the electromagnetic forces gradually decreases. In other words, the increasing air gap length would weaken the electromagnetic excitation. Therefore, the structural parameters of the motors, such as the slot opening and the air gap length, should be optimized to improve the electromagnetic characteristic.

Fig. 4Electromagnetic force under different air gap length

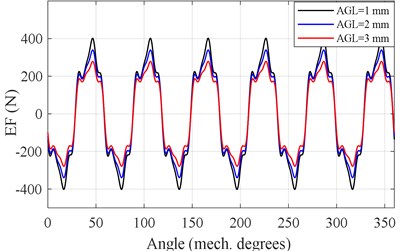
a) EF along $x$ direction

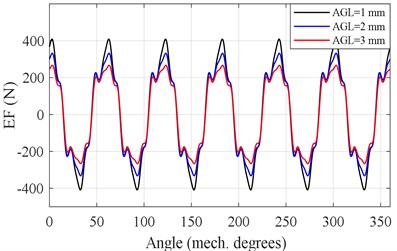
b) EF along $y$ direction

4. Conclusions

In this paper, a predicted model of the electromagnetic excitation for the BLDCM is built. Based on the obtained the vector magnetic potential, magnetic flux density of the air gap is derived, and thus the electromagnetic excitation including the electromagnetic torque and force are described. Then, the electromagnetic characteristics are analyzed according to the built model. The analysis results show that the increasing slot opening will aggravate the fluctuation of magnetic flux density, but the increasing air gap length can weaken the electromagnetic force. Therefore, the electromagnetic characteristic of the motor can be optimized using the appropriate structural parameters.

References

M. F. Unlersen, S. Balci, M. F. Aslan, and K. Sabanci, “The speed estimation via BiLSTM-based network of a BLDC motor drive for fan applications,” Arabian Journal for Science and Engineering, Vol. 47, No. 3, pp. 2639–2648, Mar. 2022, https://doi.org/10.1007/s13369-021-05700-w

Publisher
A. Zhang, Y. Bai, B. Yang, and H. Li, “Analysis of nonlinear vibration in permanent magnet synchronous motors under unbalanced magnetic pull,” Applied Sciences, Vol. 8, No. 1, p. 113, Jan. 2018, https://doi.org/10.3390/app8010113

Publisher
Z. Q. Zhu and D. Howe, “Instantaneous magnetic field distribution in brushless permanent magnet DC motors. III. Effect of stator slotting,” IEEE Transactions on Magnetics, Vol. 29, No. 1, pp. 143–151, Jan. 1993, https://doi.org/10.1109/20.195559

Publisher
F. Dubas and C. Espanet, “Analytical solution of the magnetic field in permanent-magnet motors taking into account slotting effect: no-load vector potential and flux density calculation,” IEEE Transactions on Magnetics, Vol. 45, No. 5, pp. 2097–2109, May 2009, https://doi.org/10.1109/tmag.2009.2013245

Publisher
Z. Q. Zhu, L. J. Wu, and Z. P. Xia, “An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines,” IEEE Transactions on Magnetics, Vol. 46, No. 4, pp. 1100–1115, Apr. 2010, https://doi.org/10.1109/tmag.2009.2038153

Publisher
T. Lubin, S. Mezani, and A. Rezzoug, “2-D exact analytical model for surface-mounted permanent-magnet motors with semi-closed slots,” IEEE Transactions on Magnetics, Vol. 47, No. 2, pp. 479–492, Feb. 2011, https://doi.org/10.1109/tmag.2010.2095874

Publisher
T. He, Z. Q. Zhu, F. Xu, Y. Wang, B. Hong, and L. Gong, “Influence of rotor eccentricity on electromagnetic performance of 2-pole/3-slot PM motors,” IEEE Transactions on Energy Conversion, Vol. 37, No. 1, pp. 696–706, Mar. 2022, https://doi.org/10.1109/tec.2021.3098669

Publisher

About this article

Received

22 August 2022

Accepted

27 September 2022

Published

30 September 2022

DOI

https://doi.org/10.21595/mme.2022.22950

Keywords

BLDCM

electromagnetic characteristic

slot opening

air gap length

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 51975336), Key Research and Development Program of Shandong Province (Grant No. 2020JMRH0202), the New Old Energy conversion Major Industrial Tackling Project of Shandong Province (Grant No. 2021-13), the Education and Teaching Reform Research Project of Shandong University (2022Y133, 2022Y124, 2022Y312), and Key Research and Development Program of Jining City (2021DZP005).

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2023 04 10

Discrete sliding mode control method for particle swarm optimization-based brushless DC motor of electric vehicle

Fei Wang, Qiongzhen Mei, Xiaolei Xin

Research article

2022 08 23

Analysis of unidirectional and bidirectional magnetic-thermal coupling of permanent magnet synchronous motor

Fang Ding, Aiguo Wang, Qianbin Zhang

Research article

2019 05 15

A novel hybrid topology for power quality improvement using multilevel inverter for the reduction of vibration and noise in brushless DC motor for industrial applications

Sampathkumar Ramasamy, Saravanakumar Gunasekaran, Suresh Balasubramaniam

Research article

2018 08 15

Interior noise and vibration prediction of permanent magnet synchronous motor

Kun Qian, Jintian Wang, Yang Gao, Qiang Sun, Jie Liang

Z. Li, Y. Wan, Y. Xia, F. Gong, Q. Wang, and F. Chen, “Analysis of electromagnetic characteristic in the interior permanent magnet brushless DC motor,” Mathematical Models in Engineering, Vol. 8, No. 3, pp. 91–97, Sep. 2022, https://doi.org/10.21595/mme.2022.22950

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/mme.2022.22950
UR  - https://doi.org/10.21595/mme.2022.22950
TI  - Analysis of electromagnetic characteristic in the interior permanent magnet brushless DC motor
T2  - Mathematical Models in Engineering
AU  - Li, Zhengyang
AU  - Wan, Yi
AU  - Xia, Yan
AU  - Gong, Fangbin
AU  - Wang, Qiang
AU  - Chen, Fei
PY  - 2022
DA  - 2022/09/30
PB  - JVE International Ltd.
SP  - 91-97
VL  - 8
IS  - 3
SN  - 2351-5279
SN  - 2424-4627
ER  - 

Copy Ris

Copied to clipboard!

@article{Li_2022,
	doi = {10.21595/mme.2022.22950},
	url = {https://doi.org/10.21595/mme.2022.22950},
	year = 2022,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {8},
	number = {3},
	pages = {91--97},
	author = {Zhengyang Li and Yi Wan and Yan Xia and Fangbin Gong and Qiang Wang and Fei Chen},
	title = {Analysis of electromagnetic characteristic in the interior permanent magnet brushless {DC} motor},
	journal = {Mathematical Models in Engineering}
}

Copy Bibtex

Copied to clipboard!

[1]Z. Li, Y. Wan, Y. Xia, F. Gong, Q. Wang, and F. Chen, “Analysis of electromagnetic characteristic in the interior permanent magnet brushless DC motor,” Mathematical Models in Engineering, vol. 8, no. 3, pp. 91–97, Sep. 2022, doi: 10.21595/mme.2022.22950.

Copy IEEE

Copied to clipboard!

Li, Zhengyang, Yi Wan, Yan Xia, Fangbin Gong, Qiang Wang, and Fei Chen. “Analysis of Electromagnetic Characteristic in the Interior Permanent Magnet Brushless DC Motor.” Mathematical Models in Engineering 8, no. 3 (September 30, 2022): 91–97. https://doi.org/10.21595/mme.2022.22950.

Copy Chicago

Copied to clipboard!

Analysis of electromagnetic characteristic in the interior permanent magnet brushless DC motor

Abstract

Highlights

1. Introduction

2. Analytical model of magnetic field of the BLDCM

2.1. Physical model of BLDCM

2.2. Analytical model of magnetic field

3. Analysis of electromagnetic characteristic of the BLDCM

3.1. The effect of the slot opening on the magnetic flux density (MFD)

3.2. The effect of the air gap length on the electromagnetic force

4. Conclusions

References

About this article

Related Articles