The kinematic analysis of flat lever mechanisms with application of vector calculation

Zhauyt, Algazy; Mamatova, Gulnar; Alipov, Kuanysh; Sakenova, Aizhan; Abdirova, Raushan

Vibroengineering Procedia

Browse Procedia

Published: 07 October 2016

Check for updates

The kinematic analysis of flat lever mechanisms with application of vector calculation

Algazy Zhauyt¹

Gulnar Mamatova²

Kuanysh Alipov³

Aizhan Sakenova⁴

Raushan Abdirova⁵

^{1, 2, 3, 4, 5}Kazakh National Research Technical University named after K. I. Satpayev, Almaty 050013, Kazakhstan

Corresponding Author:

Algazy Zhauyt

Cite the article Download PDF

Downloads 1513

Abstract

Linkwork, in its early applications, consisted mainly of revolute-connected members and was widely used for converting the continuous rotation of a water wheel into a reciprocating motion suited to piston pumps. The piston-cylinder combination at the end of the line represents a prismatic pair, of course, but ahead of this there are only the revolute connections generally associated with linkwork. Agricola’s arrangements show wheel and pump-power source and point of work-fairly close together. Such compactness did not always prevail; link-works of magnificent proportions were also part of the past. A linkwork is a means of power transmission as well as being a motion transformer. Before the introduction of rope transmissions and the now universal electric wire, linkwork was employed for long-distance transmission of power. Gigantic linkages, principally for mine pumping operations, connected water wheels at the riverbank to pumps high up on the hillside.

1. Introduction

The theory of synthesis of mechanisms and cars are closely connected with a task of the kinematic analysis. The unity of tasks of the analysis and synthesis is caused by coincidence of the equations defining interdependence of variables and fixed parameters of mechanisms and used in each case in their purposes [2]. Moreover, at the solution of a problem of synthesis it is necessary to use managements of kinematic analysis as restrictions. For example [1], at the solution of a problem of synthesis of directed and transmission gears of high classes it is necessary to use the kinematics equations for definition of a rotation angle $φ$ of the plane if $Q_{2}$ it isn’t set in a case when the considered problem of synthesis of the opened ABCD four-bar chain [3, 4]. Therefore, the vector method of the kinematic analysis is offered in this chapter which will be coordinated well with the method of synthesis of IKС stated in the previous chapter, and also it can independently be used for the solution of tasks on provisions, speeds and accelerations of the synthesizable mechanism [5].

2. Materials and methods

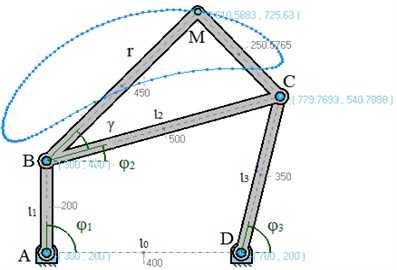
In this subsection the task of the analysis of the transfer and directing four-bar mechanisms of the II class with application of vector calculation is considered. The kinematic scheme of the transmission gear is submitted in Fig. 1. Let lengths of links $l_{0}$ , $l_{1}$ , $l_{2}$ , $l_{3}$ , and rotation angle $φ_{1}$ of an entrance link of AB are set. It is necessary to define provisions, speed and accelerations of all links.

We write down a condition of isolation of vector contour:

1

{\bar{l}}_{1} + {\bar{l}}_{2} = l_{0} + {\bar{l}}_{3} .

We enter system of coordinates $O x y z$ with single arts $\bar{i}$ , $\bar{j}$ , $\bar{k}$ . The provision of an entrance link of AB is defined in the type:

{\bar{l}}_{1} = l_{1} \{\bar{i} c o s φ_{1} + \bar{j} s i n φ_{1}\} .

Fig. 1The kinematic scheme of four-bar mechanism

We rewrite the Eq. (1) of rather unknown vectors ${\bar{l}}_{2}$ , ${\bar{l}}_{3}$ in the type:

2

{\bar{l}}_{2} - {\bar{l}}_{3} = l_{0} - {\bar{l}}_{1} = L .

The essence of an estimated method of definition of vectors ${\bar{l}}_{2}$ , ${\bar{l}}_{3}$ consists as follows. We spread out required vector ${\bar{l}}_{2}$ and ${\bar{l}}_{3}$ and on orthogonal vectors $\bar{L}$ $(\bar{k} \times \bar{L})$ :

3

\{\begin{matrix} {\bar{l}}_{2} = p_{2} \bar{L} + q_{2} (\bar{k} \times \bar{L}), \\ {\bar{l}}_{3} = p_{3} \bar{L} + q_{3} (\bar{k} \times \bar{L}), \end{matrix}

where $p_{2}$ , $q_{2}$ , $p_{3}$ , $q_{3}$ unknown coordinates of vectors ${\bar{l}}_{2}$ and ${\bar{l}}_{3}$ in new system of coordinates. We l substitute the Eq. (3) in Eq. (2), we receive:

4

(p_{2} - p_{3}) \bar{L} + (q_{2} - q_{3}) (\bar{k} \times \bar{L}) = \bar{L} .

Further considering, $q_{2} = q_{3} = q$ and $p_{2} = p$ , $p_{3} = p - 1$ system Eq. (3) we will represent in the form:

5

\{\begin{array}{l} {\bar{l}}_{2} = p \bar{L} + q_{2} (\bar{k} \times \bar{L}), \\ {\bar{l}}_{3} = (p - 1) \bar{L} + q (\bar{k} \times \bar{L}), \end{array}

where $p$ and $q$ are unknown parameters.

We determine parameters $p$ and $q$ from system Eq. (5). For this purpose, we will square both parts of the first and second equations of system Eq. (5):

6

\{\begin{array}{l} l_{2}^{2} = L^{2} (p^{2} + q^{2}), \\ l_{3}^{2} = L^{2} [{(p - 1)}^{2} + q^{2}], \end{array}

from here:

7

\{\begin{array}{l} p = \frac{1}{2} + \frac{l_{2}^{2} - l_{3}^{2}}{2 L^{2}}, \\ q = \pm [\frac{l_{2}^{2}}{L^{2}} - (\frac{1}{2} + \frac{l_{2}^{2} - l_{3}^{2}}{2 L^{2}})] . \end{array}

Here the plus and minus in the second equality correspond to different assemblies of the four-bar mechanism $A B C D$ .

The provisions of all links of the mechanism $A B C D$ can be defined from scalar products of arts of system of coordinates of $O x y z$ and the found vectors. Really, for definition of provisions $φ_{2}$ and $γ$ equalities are also fair:

8

\{\begin{array}{l} t g φ_{2} = \frac{{\bar{l}}_{2} \cdot \bar{j}}{l_{2} \cdot \bar{i}} = \frac{p L_{y} + q L_{x}}{p L_{x} - q L_{y}}, \\ t g φ_{3} = \frac{{\bar{l}}_{3} \cdot \bar{j}}{l_{3} \cdot \bar{i}} = \frac{(p - 1) L_{y} + q L_{x}}{(p - 1) L_{x} - q L_{y}}, \end{array}

where, $\bar{L} = L_{x} \cdot \bar{i} + L_{y} \cdot \bar{j}$ , ${\bar{L}}_{x} = l_{0 x} - l_{1} c o s φ_{1}$ , ${\bar{L}}_{y} = l_{0 y} - l_{1} s i n φ_{1}$ and the decision of Eq. (8) can be written down in the type:

9

\{\begin{array}{l} φ_{2} = a r c t g \frac{p L_{y} + q L_{x}}{p L_{x} - q L_{y}}, \\ φ_{3} = a r c t g \frac{(p - 1) L_{y} + q L_{x}}{(p - 1) L_{x} - q L_{y}} . \end{array}

We pass to definition of speed analogs. For this purpose we will differentiate Eq. (2) on $φ_{1}$ :

10

{\bar{l}}_{2}^{'} - {\bar{l}}_{3}^{'} = - {\bar{l}}_{1}^{'},

where:

{\bar{l}}_{2}^{'} = (\bar{k} \times {\bar{l}}_{2}) \frac{d φ_{2}}{d φ_{1}} = (\bar{k} \times {\bar{l}}_{2}) φ_{2}^{'}, {\bar{l}}_{3}^{'} = (\bar{k} \times {\bar{l}}_{3}) \frac{d φ_{3}}{d φ_{1}} = (\bar{k} \times {\bar{l}}_{3}) φ_{3}^{'}, {\bar{l}}_{1}^{'} = (\bar{k} \times {\bar{l}}_{1}),

from here:

11

\bar{k} \times {\bar{l}}_{2} φ_{2}^{'} - \bar{k} \times {\bar{l}}_{3} φ_{3}^{'} = - \bar{k} \times {\bar{l}}_{1} .

Multiplying the Eq. (11) scalarly on, ${\bar{l}}_{3}$ we will receive:

12

φ_{2}^{'} = - \frac{[{\bar{l}}_{3} \bar{k} {\bar{l}}_{1}]}{[{\bar{l}}_{3} \bar{k} {\bar{l}}_{2}]}, φ_{3}^{'} = - \frac{[{\bar{l}}_{2} \bar{k} {\bar{l}}_{1}]}{[{\bar{l}}_{3} \bar{k} {\bar{l}}_{2}]} .

Multiplying scalarly on ${\bar{l}}_{2}$ , we have similarly. We pass to definition of acceleration analogs. For this purpose we differentiate the Eq. (11) on $φ_{1}$ :

13

\bar{k} \times {\bar{l}}_{2} φ_{2}^{''} - \bar{k} \times {\bar{l}}_{2} {φ_{2}^{'}}^{2} - \bar{k} \times {\bar{l}}_{3} φ_{3}^{''} + \bar{k} \times {\bar{l}}_{3} {φ_{3}^{'}}^{2} = \bar{k} \times {\bar{l}}_{1} .

Multiplying scalarly to $l_{2}$ and $l_{3}$ , we receive analogs of accelerations of links of BC and CD in the type:

14

\{\begin{matrix} φ_{2}^{''} = \frac{({\bar{L}}_{1} l_{3})}{[{\bar{l}}_{3} \bar{k} {\bar{l}}_{2}]}, \\ φ_{3}^{''} = \frac{({\bar{L}}_{1} l_{2})}{[{\bar{l}}_{3} \bar{k} {\bar{l}}_{2}]}, \end{matrix}

where ${\bar{L}}_{1} = \bar{k} \times {\bar{l}}_{1} + \bar{k} \times {\bar{l}}_{2} {φ_{2}^{'}}^{2} - \bar{k} \times {\bar{l}}_{3} {φ_{3}^{'}}^{2}$ .

Thus, the received formulas allow to define in an explicit form provisions, speed and acceleration of all links of the transmission gear $A B C D$ .

The provision of conrod point $M$ of the link $B M$ of the directing four-bar mechanism $A B M C D$ (see Fig. 1) is defined depending on the provision of a link of $B S$ as follows:

15

{\bar{ρ}}_{M} = {\bar{l}}_{1} + \frac{r c o s γ}{l_{2}^{2}} {\bar{l}}_{2} + \frac{r s i n γ}{l_{2}^{2}} (\bar{k} \times {\bar{l}}_{2}) .

The analogs of speed and acceleration are defined by differentiation of the Eq. (15) on $φ_{1}$ :

16

\{\begin{array}{l} {\bar{ρ}}_{M}^{'} = - {\bar{l}}_{1} + \frac{r c o s γ}{l_{2}^{}} (\bar{k} \times {\bar{l}}_{2}) φ_{2}^{'} - \frac{r s i n γ}{l_{2}^{}} {\bar{l}}_{2} φ_{2}^{'}, \\ {\bar{ρ}}_{M}^{''} = - {\bar{l}}_{1} + \frac{r c o s γ}{l_{2}^{}} (\bar{k} \times {\bar{l}}_{2}) φ_{2}^{''} - \frac{r s i n γ}{l_{2}^{}} {\bar{l}}_{2} φ_{2}^{''} - \frac{r c o s γ}{l_{2}^{}} {\bar{l}}_{2} {φ_{2}^{'}}^{2} - \frac{r s i n γ}{l_{2}^{}} (\bar{k} \times {\bar{l}}_{2}) {φ_{2}^{'}}^{2} . \end{array}

The considered technique can be used for the analysis of the four-bar mechanism with forward couples. It is possible to use the received formulas and directly, having carried out limit transition with lengths of the corresponding links striving for infinity.

On the basis of the formulas removed in this paragraph the kinematic analysis of the synthesized mechanisms of the II class has been made. The second equation of system Eq. (9) has been applied at synthesis of guides and transmission gears for definition of unknown provision of the mobile plane $Q_{2}$ .

Fig. 2Computed plot of the M point position module

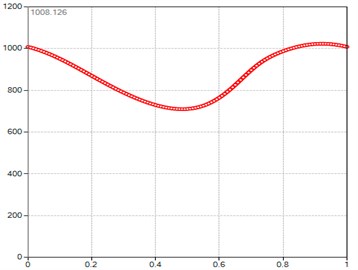
Fig. 3Computed plot of the M point velocity module

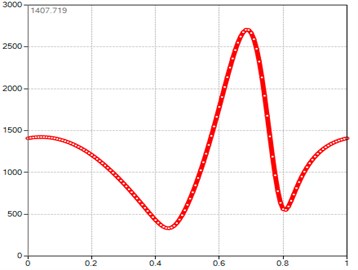
Fig. 4Computed plot of the M point acceleration module

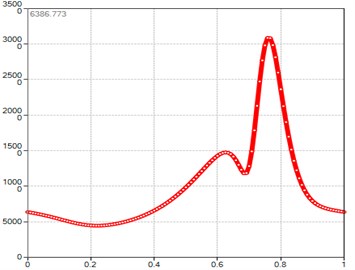
Fig. 5Computed plot of the M point tangent acceleration module

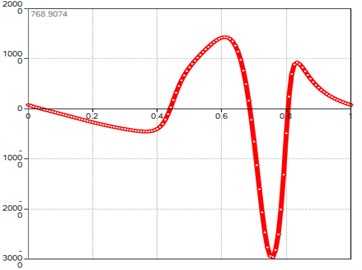
3. Results and discussion

A proper dynamic model has been developed within GIM software to provide information on the feasibility of the proposed design solution. Simulation tests have been carried out and results are discussed for validating the proposed design and characterizing its operation.

Fig. 6Computed plot of the M point normal acceleration module

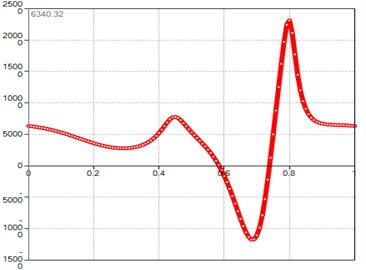
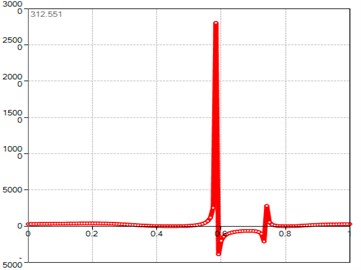
Fig. 7Computed plot of the M point curvature radius module

4. Conclusions

As practice has shown the researcher can make the procedure of drawing of mechanical system for this purpose it is necessary to calculate coordinates of characteristic points and in them to display the corresponding elements. The set of standard procedures for receiving Karina’s animation of mechanisms movement, some of them has been created for this purpose, necessary for the solution of an objective are given above. For engineers and researchers the created program has great practical value by designing directing lever mechanisms i.e. on set at the law movement point within several seconds it is possible to receive the real mechanism with animation.

References

Zhauyt Algazy The substantiating of the dynamic parameters of the shaking conveyor mechanism. Journal of Vibroengineering Procedia, Vol. 5, 2015, p. 15-20.

Search CrossRef
Joldasbekov Skanderbek, Ibraev Sayat, Zhauyt Algazy, Nurmagambetova Aiman, Imanbaeva Nurbibi Modular synthesis of plane lever six-link mechanism of high class. Middle-East Journal of Scientific Research, Vol. 21, Issue 12, 2014, p. 2339-2345.

Search CrossRef
Dobija Marta, Drewniak Józef, Zawiślak Stanisław, Shingissov Beibit, Zhauyt Algazy Countour graph application in kinematical analysis of crane mechanism. 24th International Conference on Theory of Machines and Mechatronic Systems, Poland, 2014, p. 31-32.

Search CrossRef
Zhauyt A., Kosbolov S., Shingissov B., Alymbetov A., Telesheva A., Karabashev O., Tashkenbayev A. Synthesis of four-link basic kinematic chains [BKC] with spherical pairs for spatial mechanisms. Mediterranean Journal of Social Sciences, Vol. 5, Issue 23, 2014, p. 2627-2637.

Search CrossRef
Kosbolov Serikbay, Zhauyt Algazy, Kosbolov Serikbol Kinematic synthesis of spatial linkages with spherical pairs. Journal of Theoretical and Applied Mechanics, Vol. 54, Issue 1, 2016, p. 75-85.

Search CrossRef
Kosbolov Serikbay, Duisebayeva Kulzada, Zhauyt Algazy, Buzauova Toty Synthesis of spatial lever mechanisms on the basis of the initial kinematic chains SSS pairs. Ponte, Vol. 72, Issue 2, 2016, p. 31-52.

Search CrossRef

About this article

Received

07 June 2016

Accepted

15 June 2016

Published

07 October 2016

SUBJECTS

Mechanical vibrations and applications

Keywords

computed plot

mechanism

point

machine

kinematic

simulation

four-bar mechanism

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.