Abstract
The article considers the mathematical model of a system of two electric motors. The motors are mounted on hydro mounts with magnetorheological fluid. The viscosity of the magnetorheological fluid changes when applying a magnetic field. The validity of the model is confirmed as the analysis of the balance of power in the steady state with a static load, and analysis of transient process of synchronization shaft at different coefficients of dissipative. The model allows evaluating the electrical energy consumption of electric motor in transient process.
1. Introduction
One of the perspective methods of the controlled vibration impact is magnetorheological fluid dampers [1, 2], their viscosity being changed by the magnetic field, which is created be the exciting coil. Mathematic modeling is necessary to reproduce the processes of energy consumption, transmission and transduction to process control reasonable algorithms of dampers dissipation at the electric drive operation conditions. Electromechanics conventionally displays such phenomena by ordinary differential equations – state equations which present simultaneous processes in elements of different physical nature. The task is set to form and check this system relevance on the basis of the pilot installation processes analyses [3], its asynchronous motor being equipped by out-of balance shafts junctures and mounted on an elastic foundation, which is supported by dampers with configurable dissipation.
2. Object for modeling
It is practical to apply relative units, representing variables and parameters the corresponding parts of base values. For the pilot installation having asynchronous motors 4АА56В2У3 [4] the base values, through which according to the conventional physical relations are calculated by the derived base values are shown in Table 1.
3. Mathematical model
The desk dynamic relations, having the viscosity ratio and mass together with the installed motors and other equipment basing on dampers having the equivalent dissipation ratios , in case of one asynchronous motor is presented by a set of equations [5]:
where and – the desk vibration displacement speed and together with the rotor rotation angular frequency, and – eccentricity mass and eccentricity creating the imbalance; ,, – rotating masses moment of inertia, electromagnetic torque and the moment of resistance on the shaft.
Taking into account the second one and more rotors there are added 1, 2 etc. into the first equation the correspondent items and by analogue – the pair of the latest equations reflecting the motor rotors displacement.
Table 1Key base values
Name | Parameters | ||
Notation | Value | Physical quantity | |
Voltage | 310 V | stator phase voltage amplitude | |
Current | 0.51 A | stator phase current amplitude | |
Frequency | 50 Hz | power-line frequency | |
Angular frequency | 314.1593 1/s | power-line angular frequency | |
Vector angle | 1 rad | supply voltage vector angle | |
Mass | 0.2 kg | motor rotor mass | |
Linear movement | 0.0025 m | motor rotor radius | |
Magnetorheological fluids viscosity in damper [1, 6] depends on multiple factors the main of which being the magnetic field temperature and voltage. Temperature changes take place relatively slowly and immediately not overlap the mechanical system oscillation processes. The magnetic field could be changed at milliseconds thus influencing the damper dissipation in the phase of desk vibrations and periodical current changes and linkage of the motor. In first approximation the equivalent damper dissipation ratio depending on magnetization ratio is expressed by a multinomial:
where in the given case ratios are: 1, 6, 9, 15.
In this case a 30-rate increase of value takes place within the range of the damper workload.
The electric motor receives the electrical energy from the supply net, its electromagnetic interaction of the stator and rotor shown as [7] with the coordinate transduction by a matrix equation:
connecting the transduced stator linkage and rotor along the coordinate axes and :
with the application of coordinate stator and rotor transduction matrixes:
where the system of axes frequency coincides with the angular one of three phase power supply.
In Eq. (3) the ratios, determined by standard parameters of the motor displacement scheme are used as well as the real matrix :
where , –stator and rotor active resistance, , , – rotor and stator dissipation induction as well as the main loop motor magnetization.
The transduced stator and rotor currents worked out to the single number of turns are calculated by the linkage:
using the enriched matrix of stator and rotor inductive interaction:
which due to coordinates transformation does not depend on the rotor angular displacement. The air gap torque, developed by the motor, is calculated according to the formula [4]:
where – relation of full and electromagnetic power of the asynchronous motor.
4. Power balance in static mode at different dissipation
At state Eqs. (1), (3) there were reproduced one asynchronous motor static functioning modes at a permanent load under the condition of simulated out-of-balance rotor shaft. There are considered power consumption and power requirement at different magnetization of the damper magnetorheological fluid, with a difference of the ratio relative values ranging from 1 to 30 [8]. Fig. 1 shows the assumption diagram of the motor starting at heavy damper magnetization.
It is obvious that the motor electromagnetic moment exceeds the moment of resistance in a steady-state mode. It is pre-conditioned by the enhanced damper resistance because of the increased dissipation.
Fig. 2 (as for this process) shows the instant modulus power curves: – consumed from the power source, – losses in stator and rotor active resistance, – disposed mechanical loads, – damper losses. These are calculated at the values of non-transduced stator currents and the rotor ones according to the formulas:
Fig. 2 shows that at the heavy viscosity of the magnetorheological fluid the damper losses are significant. In fact, they are proportionate to electrical loses [9]. In the case of viscosity lowering due to this fluid magnetization drop, the damper losses appear to be significantly lower than electrical losses. Active energy components calculated for the period of the supply source voltage according to the losses values are:
where , , , .
As shown in Table 2 the modeling shows that the recorded damper magnetization level increase leads to 2 times decrease in a desk vibration displacement in the considered examples.
Fig. 1The assumption diagram of the asynchronous motor starting with simulated out-of-balance rotor heavy damper magnetization
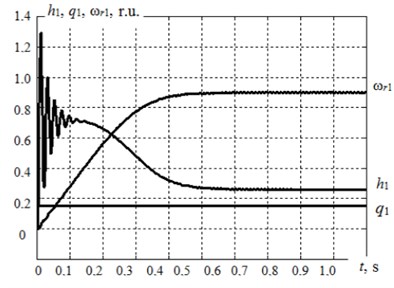
Fig. 2The assumption diagram of powers in the asynchronous functioning settled mode with out-of-balance rotor at damper heavy magnetization
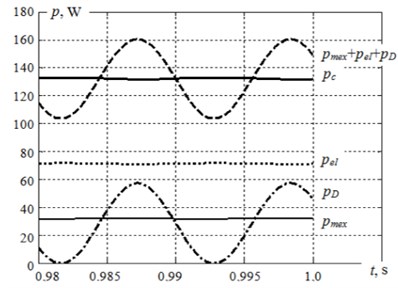
Table 2Key base values
Notation | Energy value, J | |
At heavy magnetization | At light magnetization | |
2.705 | 1.983 | |
0.647 | 0.677 | |
1.456 | 1.265 | |
0.590 | 0.067 | |
5. Dissipation influence on shafts synchronization
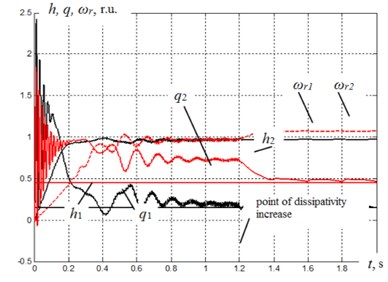
An important feature of electromechanical system operation unstable to self-synchronization [10-12] is several external power supplies, determining torque and translation movements of separate elements as well as vibrating elastic medium, through which the energy is supplied. The reproduction results of these complicated processes with the help of the proposed model correspond to the experimental results. Thus in several cases of motor start at different rotation frequencies accompanied by a go-with grab at a lower frequency and synchronization of shaft rotation, the dissipation increase leads to energy consumption increase its redistribution and in the end the break in the synchronization mode and both the motors reaching their synchronic speeds.
Fig. 3 shows an assumption diagram of the asynchronous motor starting with the angular frequency of the energy supply source 100 s-1 and the second – its frequency being 120 s-1. Within the range of 0 – 1.2 s with low damper magnetization there is obtained the mode of torque frequency at the level . At the moment 1.2 s heavy damper magnetization at the ranges is switched on, coinciding with the phase of vibration displacement speed and the break of synchronization mode take place together with the set torque frequencies.
Fig. 3Assumption diagram of displacement process of starting two asynchronous motors with synchronization of shafts speed and this mode breakdown at the increase of damper dissipation
6. Conclusions
Here is presented a valid mathematic model of the electromechanical system, providing the analysis of static and dynamic modes taking into account electrical energy consumption and redistribution at changing the damper dissipation value with the magnetorheological fluid. The method is provided to control the damper magnetic field in-phase with the exciting impact on it.
References
-
Gordeev B. А., Gordeev А. B., Kovrigin D. А., Leontyeva А. V. Hydraulic vibration mounts application in synchronous mechanical systems. Privolzhsky Nauchny Zhurnal, Vol. 3, 2009, p. 49-53.
-
Wereley N. M., Singh H. J., Choi Y. T. Magnetorheology: Advances and Applications. Royal Society of Chemistry, Cambridge, 2014.
-
Gordeev B. А., Leontyeva А. V., Osmekhin А. N., Okhulkov S. N., Bugaysky V. V. Experimental investgayion of side effects at synchronization of two engines on elastic foundation. Vestnik Mashinostroeniya, Vol. 6, 2013, p. 39-42.
-
Kravchik А. E. Asynchronous Motors of 4А Series: Reference Book. Bursa, Moscow, 2002.
-
Shreyner R. T. Mathematical modeling of alternating current drives with semiconductor frequency converters. URO RAN, Ekaterinburg, 2000.
-
Gordeev B. А., Kovrigin D. А., Leontyeva А. V. The task to synchronize a pair of engines on elastic foundation rotation. Vestnik Mashinostroeniya, Vol. 10, 2011, p. 3-7.
-
Sokolov V. V. Wave propagation in magnetic nanofluids (A Review). Acoustical Physics, Vol. 56, 2010, p. 972-988.
-
Ovchinnikov I. E., Sokolov V. V. Effect of an external magnetic field on the propagation velocities of magnetoacoustic waves in a magnetic fluid. Acoustical Physics, Vol. 55, 2009, p. 359-364.
-
Hornowski T. Ultrasonic properties of EMG-605 magnetic liquid. Proceedings SPIE Acousto-Optics and Applications V, Vol. 5828, 2005, p. 205-212.
-
Gordeev B. A., Kovrigin D. A., Leontyeva A. V. The task of synchronizing rotation of a pair of motors on an elastic foundation. Vestnik Mashinostroyeniya, Vol. 10, 2011, p. 3-7.
-
Degang W., Bo F., Hongliang Y., Bangchun W. Mathematical analysis of self-synchronous theory of vibrating system. Journal of Multidisciplinary Engineering Science and Technology, Vol. 2, 2015, p. 303-310.
-
Lai Xin, Xie Wanjun Theoretical and experimental study on electromechanical coupling properties of multihammer synchronous vibration system. Shock and Vibration, Vol. 20, 2013, p. 327-340.
About this article
The research was performed with the support of the Russian Science Foundation Grant (Project No. 15-19-10026).
