Development of a mathematical model of frequency controlled induction electric drive

Darimbaeva, Nazira; Mustafin, Marat; Almuratova, Nurgul; Zhauyt, Algazy

doi:10.21595/jve.2021.22051

Journal of Vibroengineering

Browse Journal

Submit article

Published: 09 September 2021

Check for updates

Development of a mathematical model of frequency controlled induction electric drive

Nazira Darimbaeva¹

Marat Mustafin²

Nurgul Almuratova³

Algazy Zhauyt⁴

^{1, 2, 3}Department of Electrical Machines and Electric Drive, Almaty University of Power Engineering and Telecommunications, Almaty, Kazakhstan

⁴Department of Electronics and Robotics, Almaty University of Power Engineering and Telecommunications, Almaty, Kazakhstan

Corresponding Author:

Marat Mustafin

Cite the article Download PDF

Downloads 751

Abstract

A mathematical model of a frequency-controlled induction (asynchronous) electric drive is proposed, which makes it possible to study electromagnetic and electromechanical processes in an electric drive with any drive mechanism and takes into account the non-sinusoidality of the output voltage of the frequency converter. The block diagram of the algorithms of calculations performed in the “Mathcad” computer application, the results of modeling and their analysis are presented.

Development of a mathematical model of frequency controlled induction electric drive

1. Introduction

At present, the most massive consumers of electrical energy are electric drives based on Induction (asynchronous) electric motors (IM). At the design stages of new and modernization of existing electric drives with IM, an important place is occupied by mathematical modeling of the object [1]. The mathematical description of the electromagnetic and electromechanical processes of an induction electric drive has been known for a long time [2]. Different authors and at different times have used different approaches, methods of analysis, forms of mathematical description of stationary and dynamic modes of operation of induction drive systems [3]. However, the existing models of the electric drive with IM either do not take into account the features of the driven mechanism or designed for one type of mechanisms [5]. So, in, a model of an induction drive for centrifugal mechanisms with a quadratic dependence of the torque resistance on speed is proposed [6]. The authors propose the universalization of the mathematical model of the electric drive in order to use it for mechanisms with any torque resistance. In addition, in the known models, one of the assumptions was the sinusoidality of the supply voltage of the IM. In reality, the output voltage of frequency converters contains higher harmonic components [7-9], leading to distortion of the shape of the motor currents and the electromagnetic torque. The article proposes to supplement the asynchronous motors (AM) model in order to take into account the real form of voltages and currents in a frequency-controlled electric drive [10]. The model, created on the basis of the computer mathematical application “Mathcad”, and this model is quite universal, since it covers all options for IM control. By setting the necessary initial conditions [11], all types of transient processes (start, stop, reverse, load shedding and surge) are modeled, various forms of setting influences for their formation. Calculation of instantaneous values of currents, torques, and powers is accompanied by the calculation of integral characteristics - powers during the transient process, power factors and efficiency [12]. The complete system of initial differential equations describing the processes in the induction electric drive of centrifugal pumps consists of three groups: the equations of electromagnetic equilibrium (Kirchhoff), which describe the electromagnetic processes in the engine, the equations of electromechanical energy conversion, and the equations characterizing the features of the mechanical load on the motor shaft [13-15].

2. Materials and methods

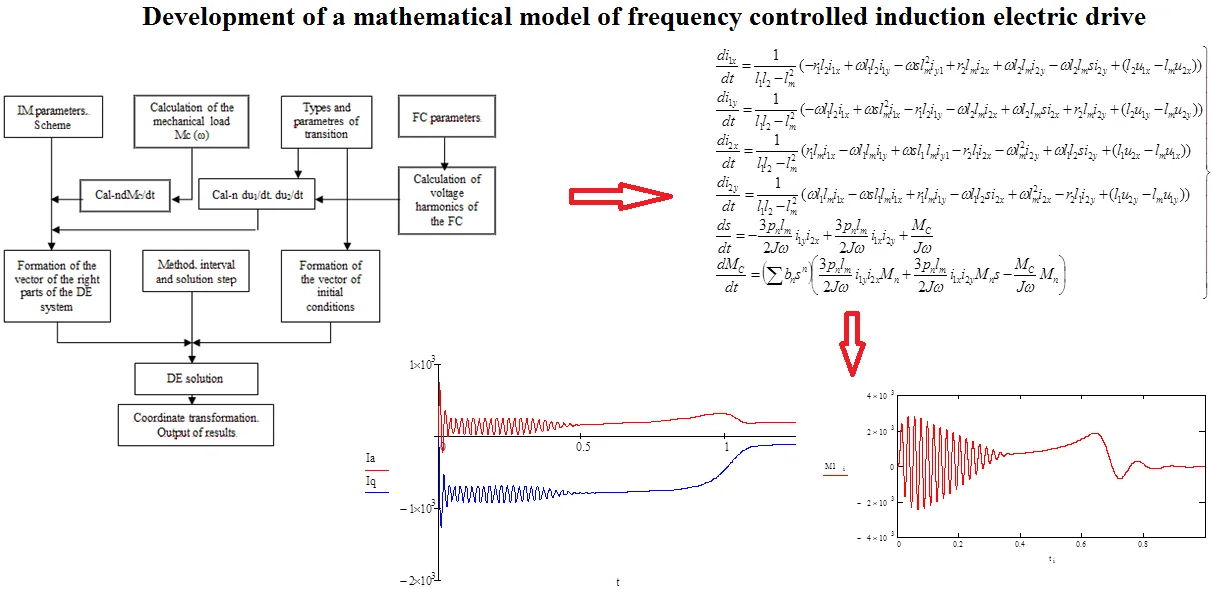
Fig. 1 shows a block diagram of the mathematical model of an electric drive based on IM. The added blocks for calculating the mechanical load and the parameters of the frequency converter, which are discussed in this article, are highlighted here [16].

Fig. 1Block diagram of the mathematical model

The model described in includes a mandatory block of electromechanical conversions in the drive [1]. In general, the electromechanical relations in the program are calculated by the components of the equation of motion of the electric drive:

1

M - M_{C} = J \frac{d ω}{d t} .

In Eq. (1), the electromagnetic torque developed by the engine is determined quite simply:

2

M = - \frac{3}{2} p_{n} l_{m} |\begin{array}{l} i_{1 x} & i_{2 x} \\ i_{1 y} & l_{2 y} \end{array}| .

To determine the dependence $M_{c} (ω)$ , it is necessary to carry out a calculation and analysis of mechanical characteristics for each investigated mechanism. For example, under centrifugal loading, the moment of resistance of the $M_{C}$ mechanism is a complex function of speed [17]. In addition, for the numerical solution of the system of differential equations of the drive, it is necessary to write in an analytical form (calculate) the first derivative ( $d M_{C} / d t$ value). In this case, various types of simplifications and assumptions are used that reduce the accuracy of the simulation results.

In [1], for instance, $d M_{C} / d t$ calculated as:

\frac{d M_{C}}{d t} = \frac{d M_{C}}{d s} \frac{d s}{d t},

\frac{d s}{d t} = - \frac{1}{ω_{0}} \frac{d ω}{d t} = - \frac{1}{J ω_{0}} (\frac{3 p_{n} l_{m}}{2} (i_{1 y} i_{2 x} - i_{1 x} i_{2 y}) - M_{C}) .

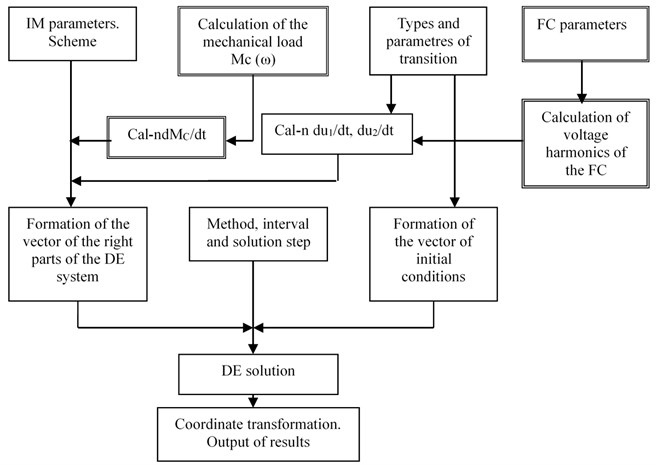
In the proposed model, it has been proposed to unify this calculation by making it applicable for any dependence $M_{c} (ω) .$ The mechanical characteristic of the most mechanisms is a continuous “smooth” function without jumps and discontinuities and, therefore, this can be approximated by a polynomial function [18]. The computer mathematical application “Mathcad” has a number of built-in functions that simplify this solution. One of the is used in the developed model. Let $M_{C}$ change during speed regulation according to a nonlinear dependence, uncertain analytically. It is determined experimentally or according to the passport characteristics presented by the manufacturer in the form of graphs or Tables. Fig. 2 shows two such characteristics corresponding to a mechanism with a constant power on the motor shaft ( $M_{c 1}$ ) and with a “fan” load ( $M_{c 2}$ ).

Fig. 2Changes in the moment of resistance

In the “Calculation of mechanical load” block, the mechanical characteristic presented in the form of a table is converted into a polynomial regression of the form:

3

M c (ω) = b_{0} + b_{1} ω + b_{2} ω^{2} + . . + b_{n} ω^{n} .

Next, the value of $d M p / d ω$ is calculated, which in our case has the form:

4

d M c (ω) / d ω = b_{1} + {2 b}_{2} ω + {3 b}_{3} ω^{2} + . . + n b_{n} ω^{n - 1}

Fig. 3 shows a fragment of the program and the results of the calculation in the “Calculation of mechanical load” block for an object with a mechanical characteristic $M_{c 1}$ .

Fig. 3Fragment of the program “Calculation of mechanical load”

In the program, the dependence $M_{c} (ω)$ is presented in the form of the ММ1 vector. To solve the problem, the program “ $r e g r e s s (X, Y, k)$ ” is used which built into Mathcad, which returns the vector “coeffs” containing the coefficients of the $k$ degree polynomial, which best approximates the “cloud” of points with coordinates stored in vectors $X$ and $Y$ .

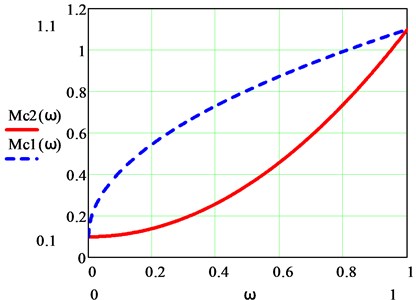
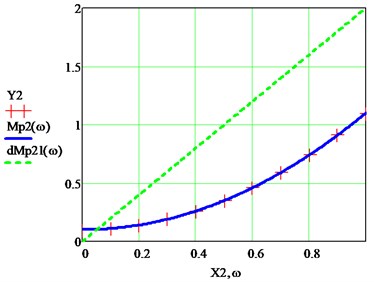
Graphical interpretation of the result is shown in Fig. 4. Tabular values of the mechanical characteristics ( $X$ , $Y$ , indicated by crosses) are approximated with high accuracy by the polynomial $M_{p} (ω)$ . The calculated derivative $d M_{p} (ω)$ is also shown here [19].

To obtain the characteristics of any other mechanism in the initial data of the program, it is enough to set the tabular data of its mechanical characteristics. In the figure below (see Fig. 5) the calculation results for the mechanism with the “fan” load $M_{c 2}$ are shown [20].

Fig. 4Exact approximation of the polynomials Mpω and dMp(ω)

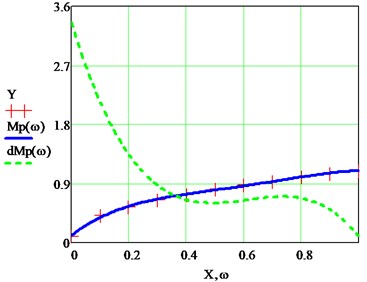
Fig. 5Fan load moment of resistance

In accordance with the proposed changes, the block for solving the system of differential equations of the mathematical model of an electric drive with IM takes the form:

5

\{\begin{array}{l} \frac{d i_{1 x}}{d t} = \frac{1}{l_{1} l_{2} - l_{m}^{2}} (- r_{1} l_{2} i_{1 x} + ω l_{1} l_{2} i_{1 y} - ω s l_{m}^{2} i_{y 1} + r_{2} l_{m} i_{2 x} \\ + ω l_{2} l_{m} i_{2 y} - ω l_{2} l_{m} s i_{2 y} + (l_{2} u_{1 x} - l_{m} u_{2 x})), \\ \frac{d i_{1 y}}{d t} = \frac{1}{l_{1} l_{2} - l_{m}^{2}} (- ω l_{1} l_{2} i_{1 x} + ω s l_{m}^{2} i_{1 x} - r_{1} l_{2} i_{1 y} - ω l_{2} l_{m} i_{2 x} \\ + ω l_{2} l_{m} s i_{2 x} + r_{2} l_{m} i_{2 y} + (l_{2} u_{1 y} - l_{m} u_{2 y})), \\ \frac{d i_{2 x}}{d t} = \frac{1}{l_{1} l_{2} - l_{m}^{2}} (r_{1} l_{m} i_{1 x} - ω l_{1} l_{m} i_{1 y} + ω s l_{1} l_{m} i_{y 1} - r_{2} l_{1} i_{2 x} \\ - ω l_{m}^{2} i_{2 y} + ω l_{1} l_{2} s i_{2 y} + (l_{1} u_{2 x} - l_{m} u_{1 x})), \\ \frac{d i_{2 y}}{d t} = \frac{1}{l_{1} l_{2} - l_{m}^{2}} (ω l_{1} l_{m} i_{1 x} - ω s l_{1} l_{m} i_{1 x} + r_{1} l_{m} i_{1 y} - ω l_{1} l_{2} s i_{2 x} \\ + ω l_{m}^{2} i_{2 x} - r_{2} l_{1} i_{2 y} + (l_{1} u_{2 y} - l_{m} u_{1 y})), \\ \frac{d s}{d t} = - \frac{3 p_{n} l_{m}}{2 J ω} i_{1 y} i_{2 x} + \frac{3 p_{n} l_{m}}{2 J ω} i_{1 x} i_{2 y} + \frac{M_{C}}{J ω}, \\ \frac{d M_{C}}{d t} = (\sum b_{n} s^{n}) {(\frac{3 p_{n} l_{m}}{2 J ω} i_{1 y} i_{2 x} M_{n} + \frac{3 p_{n} l_{m}}{2 J ω} i_{1 x} i_{2 y} M_{n} s - \frac{M_{C}}{J ω} M_{n})}_{} . \end{array}

Fig. 6 and Fig. 7 show the dependences of the torque resistance $M_{c 1} (t)$ and $M_{c 2} (t)$ at the start of the IM, obtained on this model.

The curves of the IM electromagnetic torque at start-up with various types of loads, obtained on the proposed model, are presented in Fig. 8 and Fig. 9.

Fig. 6Dependence of the moment of resistances Mc1t at the state of the IM

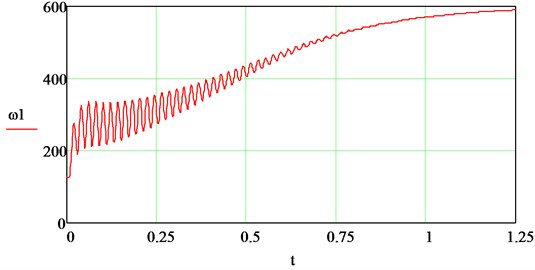
Fig. 7Dependence of the moment of resistances Mc2t at the start of the IM

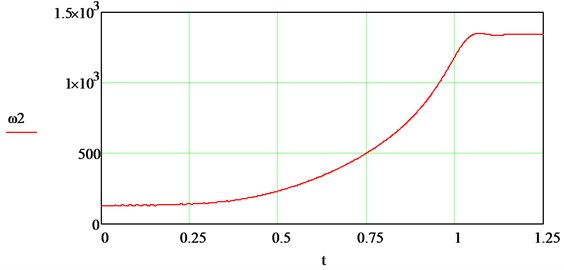
Fig. 8Electromagnetic moment of IM at start with MC1

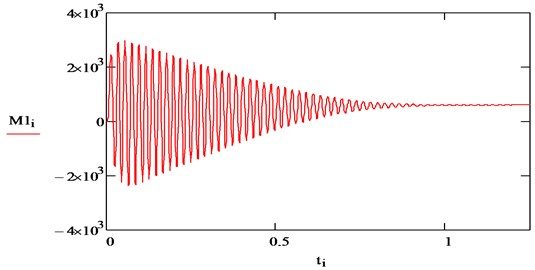
Fig. 9Electromagnetic moment of IM at start with MC2

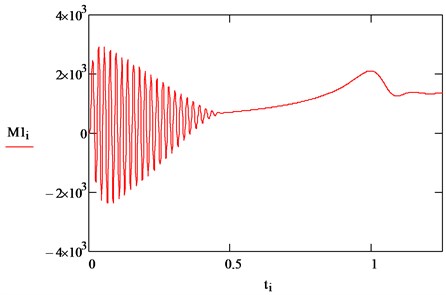
3. Results and discussion

The obtained curves correspond to the concept of transient processes in an electric drive at the torque resistance of the mechanism, depending on the speed of the motor shaft, as well as to the mechanisms considered in the article (see Fig. 2). The results of simulating a drive with a centrifugal load (Fig. 7-9) coincide with the results obtained in on a model of an induction electric drive of a centrifugal pump [1]. In the previous model, one of the assumptions was the sinusoidality of the supply voltage of the IM. In reality, the output voltage of frequency converters contains higher harmonic components, leading to distortion of the shape of the motor currents and the electromagnetic torque [2]. The article proposes to supplement the IM model in order to take into account the real form of voltages and currents in a frequency-controlled electric drive. For this, the system is supplemented with equations that reflect the output parameters and properties of power supplies [5]. The block diagram adds two blocks (“Frequency converter parameters” and “Calculation of harmonics of the inverter voltage”), in which the harmonic analysis of the inverter output voltage is carried out and the obtained values are converted into synchronous coordinates $x$ , $y$ . In the calculations, we use the basic concepts of the vector-harmonic method for analyzing electromagnetic processes in IM. It is known that the higher harmonic components of voltages and currents can, like the first harmonics, be represented by vectors rotating with a frequency that is a multiple of the order of harmonics, and, therefore, they can be transformed in different coordinate systems. This makes it possible to use the same algorithms and formulas for calculating the distorting components of motor currents as for calculating electromagnetic processes in IM by the first harmonics. For $ν$ - $х$ harmonic components of IM currents and voltages, the equation of electrical equilibrium Eq. (1) retains the structure:

6

|\begin{matrix} U_{1 x υ}^{} \\ U_{1 y υ}^{} \\ 0 \\ 0 \end{matrix}| = |\begin{matrix} r_{1} + p (l_{1} + l_{m}) & - ω_{υ} (l_{1} + l_{m}) & p l_{m} & - ω_{υ} l_{m} \\ ω_{υ} (l_{1} + l_{m}) & r_{1} + p_{n} (l_{1} + l_{m}) & ω_{υ} l_{m} & p_{n} l_{m} \\ p_{n} l_{m} & - ω_{υ} s_{ν} l_{m} & r_{2} p_{n} (l_{2} + l_{m}) & - ω_{υ} s_{ν} (l_{2} + l_{m}) \\ ω_{υ} s_{ν} l_{m} & p_{n} l_{m} & ω_{υ} s_{ν} (l_{2} + l_{m}) & r_{2} (l_{2} + l_{m}) \end{matrix}| |\begin{array}{l} I_{1 x υ}^{} \\ I_{1 y υ}^{} \\ I_{2 x υ}^{} \\ I_{2 y υ}^{} \end{array}|,

where $ν$ – is the serial number of the harmonic component of current and voltage; $U_{1 x ν}$ – is the projection of the $ν$ -th harmonic of stator voltage on the $x$ -axis; $U_{1 y ν}$ – is the projection of the $ν$ -th harmonic of the stator voltage onto the $y$ -axis; $I_{1 x ν}$ , $I_{1 y ν}$ – is the projections of the $ν$ -th harmonic of the stator current, respectively, on the $x$ and $y$ axes; $I_{2 x ν}$ , $I_{2 y ν}$ – is the projections of the $ν$ -th harmonic of the rotor current, respectively, on the $x$ and $y$ axes; $l_{1}$ , $l_{2}$ – is the phase leakage inductance of the stator and rotor; $l_{m}$ – is the inductance of the magnetizing circuit; $ω$ – is the angular frequency of rotation of the rotor; $r_{1}$ , $r_{2}$ – is the active resistances of the stator and rotor phases; $ω_{ν}$ – is the rotation frequency $ν$ -th harmonic component.

The difference from the first harmonic equation is as follows [1]. In Eq. (6), the value of $s_{ν}$ appears – slip relative to higher harmonic ones:

7

S_{ν} = \frac{ω_{ν} \pm ω}{ω_{ν}} .

In Eq. (7), the minus sign refers to the harmonic components of the positive sequence (including the first harmonic), the plus sign refers to the harmonic negative sequence, the vector of which rotates in the opposite direction.

In the equations of electromechanical energy conversion, the time derivative of $s_{ν}$ :

8

\frac{d s_{ν}}{d t} = - \frac{1}{ω_{ν}} \frac{d ω}{d t} = - \frac{1}{J ω_{ν}} (\frac{3 p_{n} l_{m}}{2} (i_{1 y ν} i_{2 x ν} - i_{1 x ν} i_{2 y ν}) - M_{C}) .

In the program for calculating the dynamic characteristics of the centrifugal mechanism drive, the quadratic dependence of the moment of resistance on the rotation frequency was used.

One more equation in the system ( $d M_{C} / d t$ value) is obtained by differentiating the equation of motion of the electric drive with a quadratic dependence of the moment of resistance on the rotation frequency [12]:

9

\frac{d M_{C}}{d t} = \frac{d M_{C}}{d s_{ν}} \frac{d s_{ν}}{d t} = (- 2 M_{n} + 2 M_{n} s_{ν}) [- \frac{1}{J ω_{ν}} (\frac{3 p_{n} l_{m}}{2} (i_{1 y ν} i_{2 x ν} - i_{1 x ν} i_{2 y ν}) - M_{C})] .

As a result, taking into account expressions Eqs. (6-9), the system of equations of an asynchronous electric drive takes the form:

10

\{\begin{array}{l} \frac{d i_{1 x ν}}{d t} = \frac{1}{l_{1} l_{2} - l_{m}^{2}} (- r_{1} l_{2} i_{1 x ν} + ω_{ν} l_{1} l_{2} i_{1 y ν} - ω_{ν} s_{ν} l_{m}^{2} i_{y 1 ν} + r_{2} l_{m} i_{2 x ν} \\ + ω_{ν} l_{2} l_{m} i_{2 y ν} - ω_{ν} l_{2} l_{m} s_{ν} i_{2 y ν} + (l_{2} u_{1 x ν} - l_{m} u_{2 x ν})), \\ \frac{d i_{1 y ν}}{d t} = \frac{1}{l_{1} l_{2} - l_{m}^{2}} (- ω_{ν} l_{1} l_{2} i_{1 x ν} + ω_{ν} s_{ν} l_{m}^{2} i_{1 x ν} - r_{1} l_{2} i_{1 y ν} - ω_{ν} l_{2} l_{m} i_{2 x ν} \\ + ω_{ν} l_{2} l_{m} s_{ν} i_{2 x ν} + r_{2} l_{m} i_{2 y ν} + (l_{2} u_{1 y ν} - l_{m} u_{2 y ν})), \\ \frac{d i_{2 x ν}}{d t} = \frac{1}{l_{1} l_{2} - l_{m}^{2}} (r_{1} l_{m} i_{1 x ν} - ω_{ν} l_{1} l_{m} i_{1 y ν} + ω_{ν} s_{ν} l_{1} l_{m} i_{y 1 ν} - r_{2} l_{1} i_{2 x ν} \\ - ω_{ν} l_{m}^{2} i_{2 y ν} + ω_{ν} l_{1} l_{2} s_{ν} i_{2 y ν} + (l_{1} u_{2 x ν} - l_{m} u_{1 x ν})), \\ \frac{d i_{2 y ν}}{d t} = \frac{1}{l_{1} l_{2} - l_{m}^{2}} (ω_{ν} l_{1} l_{m} i_{1 x ν} - ω_{ν} s_{ν} l_{1} l_{m} i_{1 x ν} + r_{1} l_{m} i_{1 y ν} - ω_{ν} l_{1} l_{2} s_{ν} i_{2 x ν} \\ + ω_{ν} l_{m}^{2} i_{2 x ν} - r_{2} l_{1} i_{2 y ν} + (l_{1} u_{2 y ν} - l_{m} u_{1 y ν})), \\ \frac{d s_{ν}}{d t} = - \frac{3 p_{n} l_{m}}{2 J ω_{ν}} i_{1 y ν} i_{2 x ν} + \frac{3 p_{n} l_{m}}{2 J ω_{ν}} i_{1 x ν} i_{2 y ν} + \frac{M_{C}}{J ω_{ν}}, \\ \frac{d M_{C}}{d t} = \frac{3 p_{n} l_{m}}{J ω_{ν}} i_{1 y ν} i_{2 x ν} M_{n} - \frac{3 p_{n} l_{m}}{J ω_{ν}} i_{1 y ν} i_{2 x ν} M_{n} s_{ν} - \frac{3 p_{n} l_{m}}{J ω_{ν}} i_{1 x ν} i_{2 y ν} M_{n} \\ + \frac{3 p_{n} l_{m}}{J ω_{ν}} i_{1 x ν} i_{2 y ν} M_{n} s_{ν} - \frac{2 M_{C}}{J ω_{ν}} M_{n} + \frac{2 M_{C}}{J ω_{ν}} M_{n} s_{ν} . \end{array}

Figs. 10-14 show the results of calculations of transient processes taking into account the nonsinusoidality of the output voltage of the inverter by the example of starting an asynchronous motor with a squirrel-cage rotor.

Fig. 10Active and reactive components of the IM stator current (first harmonics)

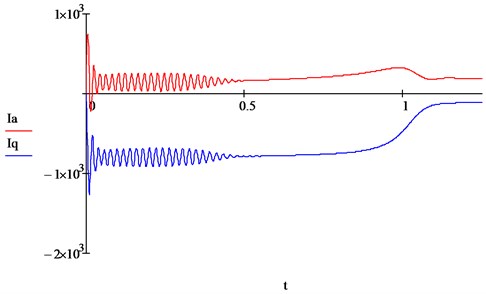
Fig. 11a) Speed and b) torque IM (first harmonics)

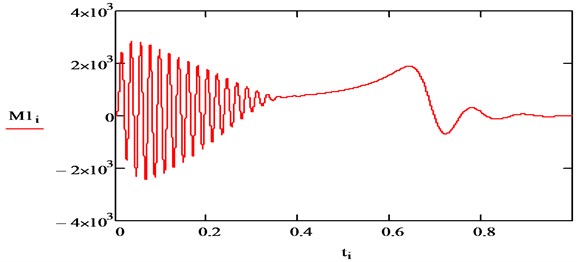
a)

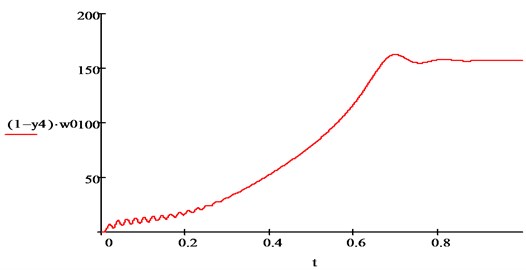
b)

The curves of the transient process for the first harmonics (see Figs. 2-3) are similar to the results obtained in [1], which confirms the adequacy of the model. For calculations for higher harmonic voltages and currents, a frequency converter with a controlled rectifier, made according to a 6-pulse (bridge) circuit, is adopted [13-15]. The output voltage of such an inverter contains higher harmonic components of the order of: $ν = 6 n \pm 1$ , where $n =$ 1, 2,….

Figs. 4-6 show the results of modeling of transient processes for the seventh harmonics. The frequency and attenuation of the components of the higher harmonics of the stator current of the IM correspond to the well-known concepts of electrical engineering.

Fig. 12Active and reactive components of the AM stator current (seventh harmonic)

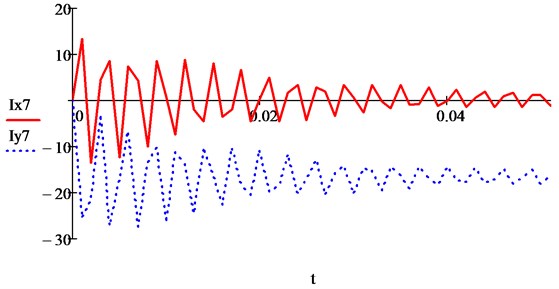
Fig. 13 shows the curve of the change in the electromagnetic torque of the IM from the interaction of the seventh harmonics of currents, calculated by the formula:

11

M_{7} = \frac{3}{2} p_{n} L_{m} (i_{1 y 7} i_{2 x 7} - i_{1 x 7} i_{2 y 7}) .

Fig. 13Electromagnetic moment of IM from the interaction of seventh harmonics

Obviously, the value of such a torque (1.1 Nm) is negligible (the nominal torque of the IM in the model is 1200 Nm). But in the engine, as a result of the interaction of harmonic flux and currents of different orders, pulsating moments are formed [16]. Their main source is the interaction of the main flow with the higher harmonic components of the rotor current:

M_{1, ν} = {\bar{Ф}}_{1} \cdot {\bar{i}}_{2 ν},

or for the interaction of 1st and 7th harmonics:

12

M_{1,7} = \frac{3}{2} p_{n} L_{m} (i_{1 y} i_{2 x 7} - i_{1 x} i_{2 y 7}) .

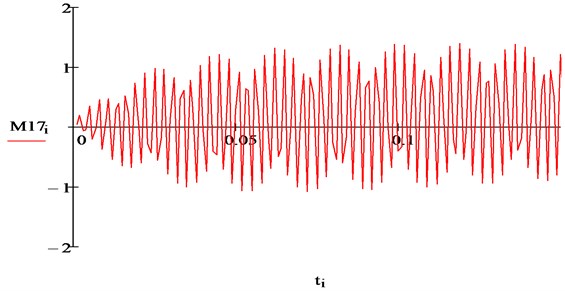
The curve of the IM electromagnetic moment calculated according to Eq. (12) is shown in Fig. 6.

Fig. 14Electromagnetic moment of IM from the interaction of the first and seventh harmonics

The amplitude of oscillations of the electromagnetic moment is 115 Nm, i.e. up to 9 % of the nominal value [17, 18]. The total pulsating moment from the interaction of the main flow with all harmonic currents of the rotor can be determined as conclusions:

M_{1, ν} = \frac{3}{2} p_{n} L_{m} \sum_{ν = 1}^{\infty} ‍ (i_{1 y} i_{2 x ν} - i_{1 x} i_{2 y ν}) .

As a result of the further development of the mathematical model of an adjustable induction electric drive, it becomes possible to use the model to study electric drives of mechanisms with any moment of resistance with minimal preparation of data on the load [19]. At the same time, the adequacy of the model is preserved with a high accuracy of representation of the real mechanical characteristics of the driven mechanism, obtained experimentally or from the manufacturer, by a polynomial [20]. The model allows, in addition to options for IM control, types of transient processes, the nature of the load, to take into account the features of the circuit and the principle of operation of the frequency converter.

4. Conclusions

The mathematical model proposed in the article, in addition to the blocks describing electromagnetic and electromechanical processes in an asynchronous motor, includes blocks for calculating the mechanical load and parameters of the frequency converter. The frequency converter (FC) parameter block calculates the harmonic composition of the FC output voltage and prepares data for calculating the highest harmonic components of the IM currents. As a result, the currents and the electromagnetic moment of the IM are calculated taking into account the real (non-sinusoidal) form of the FC voltage. In this case, the calculation is possible for any circuit solution and method of forming the FC voltage. The proposed upgrade allows not only to refine the calculation of the dynamic and static characteristics of the electric drive, but also to assess the impact of the properties of the FC on its energy performance. Taking into account the change in the mechanical load on the motor shaft when adjusting its speed presents significant difficulties. In the proposed model, it is proposed to unify the mathematical description of the mechanical characteristics of the working mechanism. To do this, in the mechanical load calculation block, the entered tabular load data is converted into the coefficients of a polynomial of a given degree, which most accurately approximates the mechanical characteristic of any complexity. The obtained result is further used in solving the equation of motion of the electric drive. As a result, it becomes possible to use the model to study electric drives of mechanisms with any moment of resistance with minimal preparation of load data. Thus, a mathematical model of an adjustable asynchronous electric drive is obtained, which allows, in addition to options for controlling the IM, types of dynamic and stationary processes, to adequately take into account the features of the circuit and the principle of operation of the frequency converter, as well as the features of the mechanical load of any complexity.

References

Mustafin M. and Almuratova N., “Calculation of transient processes of electric drives of centrifugal mechanisms,” International Journal of Pharmacy and Technology, Vol. 8, No. 3, pp. 17745–17756, 2016.

Search CrossRef
L. S. Bocii and V. Muller, “Mathematic model of three-phase induction machine connected to advanced inverter for traction system for electric trolley,” Anais da Academia Brasileira de Ciências, Vol. 85, No. 2, pp. 849–858, May 2013, https://doi.org/10.1590/s0001-37652013005000028

Publisher
A. P. Mark, R. Vairamani, and G. C. R. Irudayaraj, “Mathematical modeling and analysis of different vector controlled CSI fed 3-phase induction motor drive,” Journal of Applied Mathematics, Vol. 2014, pp. 1–13, 2014, https://doi.org/10.1155/2014/623982

Publisher
K. P. Phillips, “Current-source converter for AC motor drives,” IEEE Transactions on Industry Applications, Vol. IA-8, No. 6, pp. 679–683, Nov. 1972, https://doi.org/10.1109/tia.1972.349851

Publisher
M. Veerachary, “Optimal control strategy for a current source inverter fed induction motor,” Computers and Electrical Engineering, Vol. 28, No. 4, pp. 255–267, Jul. 2002, https://doi.org/10.1016/s0045-7906(00)00051-3

Publisher
M. Salo and H. Tuusa, “A vector-controlled PWM current-source-inverter-fed induction motor drive with a new stator current control method,” IEEE Transactions on Industrial Electronics, Vol. 52, No. 2, pp. 523–531, Apr. 2005, https://doi.org/10.1109/tie.2005.844243

Publisher
M. Babaei and H. Heydari, “Direct torque control of pulse width modulation current source inverter-fed induction motor by novel switching method,” Electric Power Components and Systems, Vol. 38, No. 5, pp. 514–532, Mar. 2010, https://doi.org/10.1080/15325000903376933

Publisher
D. G. Holmes, B. P. Mcgrath, and S. G. Parker, “Current regulation strategies for vector-controlled induction motor drives,” IEEE Transactions on Industrial Electronics, Vol. 59, No. 10, pp. 3680–3689, Oct. 2012, https://doi.org/10.1109/tie.2011.2165455

Publisher
O. Kuznyetsov, “Mathematical model of a three-phase induction machine in a natural abc reference frame utilizing the method of numerical integration of average voltages at the integration step and its application to the analysis of electromechanical systems,” Mathematical Problems in Engineering, Vol. 2019, pp. 1–13, Dec. 2019, https://doi.org/10.1155/2019/4581769

Publisher
A. Dineva et al., “Review of soft computing models in design and control of rotating electrical machines,” Energies, Vol. 12, No. 6, p. 1049, Mar. 2019, https://doi.org/10.3390/en12061049

Publisher
D. Wang, X. Yuan, and M. Zhang, “Power-balancing based induction machine model for power system dynamic analysis in electromechanical timescale,” Energies, Vol. 11, No. 2, p. 438, Feb. 2018, https://doi.org/10.3390/en11020438

Publisher
A. Parizad, S. Mohamadian, M. E. Iranian, and J. M. Guerrero, “Power system real-time emulation: a practical virtual instrumentation to complete electric power system modeling,” IEEE Transactions on Industrial Informatics, Vol. 15, No. 2, pp. 889–900, Feb. 2019, https://doi.org/10.1109/tii.2018.2837079

Publisher
M. Dagbagi, A. Hemdani, L. Idkhajine, M. W. Naouar, E. Monmasson, and I. Slama-Belkhodja, “ADC-based embedded real-time simulator of a power converter implemented in a low-cost FPGA: application to a fault-tolerant control of a grid-connected voltage-source rectifier,” IEEE Transactions on Industrial Electronics, Vol. 63, No. 2, pp. 1179–1190, Feb. 2016, https://doi.org/10.1109/tie.2015.2491883

Publisher
M. D. Omar Faruque et al., “Real-time simulation technologies for power systems design, testing, and analysis,” IEEE Power and Energy Technology Systems Journal, Vol. 2, No. 2, pp. 63–73, Jun. 2015, https://doi.org/10.1109/jpets.2015.2427370

Publisher
L. Wang et al., “Methods of interfacing rotating machine models in transient simulation programs,” IEEE Transactions on Power Delivery, Vol. 25, No. 2, pp. 891–903, Apr. 2010, https://doi.org/10.1109/tpwrd.2009.2039809

Publisher
M. Y. Pustovetov, “Approach to computer implementation of mathematical model of 3-phase induction motor,” IOP Conference Series: Materials Science and Engineering, Vol. 327, p. 022085, Mar. 2018, https://doi.org/10.1088/1757-899x/327/2/022085

Publisher
M. Sokola and E. Levi, “A novel induction machine model and its application in the development of an advanced vector control scheme,” The International Journal of Electrical Engineering and Education, Vol. 37, No. 3, pp. 233–248, Jul. 2000, https://doi.org/10.7227/ijeee.37.3.3

Publisher
S. E. Zirka, Y. I. Moroz, and C. M. Arturi, “Accounting for the influence of the tank walls in the zero-sequence topological model of a three-phase, three-limb transformer,” IEEE Transactions on Power Delivery, Vol. 29, No. 5, pp. 2172–2179, Oct. 2014, https://doi.org/10.1109/tpwrd.2014.2307117

Publisher
Maksimkina J., “Direct start-up of the squirrel-cage induction motor at variable parameters of the rotor,” Latvian Journal of Physics and Technical Sciences, Vol. 50, No. 1, pp. 10–21, 2013.

Search CrossRef
Benecke M., Doebbelin R., Griepentrog G., and Lindemann A., “Skin effect in squirrel cage rotor bars and its consideration in simulation of non-steady-state operation of induction machines,” in Progress in Electromagnetics Research Symposium Proceedings, pp. 1451–1455, 2011.

Search CrossRef

About this article

Received

12 May 2021

Accepted

18 August 2021

Published

09 September 2021

SUBJECTS

Dynamics and oscillations in electrical and electronics engineering

DOI

https://doi.org/10.21595/jve.2021.22051

Keywords

mathematical modeling

induction motor

characteristic

frequency

energy

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 08 06

A numerical study of rotor eccentricity and dynamic load in induction machines for motor current analysis based diagnostics

Haiyang Li, Zhexiang Zou, Xiuquan Sun, Fengshou Gu, Andrew D. Ball

Research article

2021 06 28

Active reduction of magnetic noise occurring in the stators of an induction motors

Artem Ermolaev, Vladimir Erofeev, Alexandr Plekhov, Dmitriy Titov

Research article

2021 06 21

Sucker rod pump frequency-elastic drive mode development – from the numerical model to the field test

Clemens Langbauer, Thomas Langbauer, Rudolf Fruhwirth, B. Mastobaev

Research article

2021 01 06

Induction motor pre-excitation starting based on vector control with flux linkage deviation decoupling

Zhe Cao, Jingzhuo Shi, Bo Fan

N. Darimbaeva, M. Mustafin, N. Almuratova, and A. Zhauyt, “Development of a mathematical model of frequency controlled induction electric drive,” Journal of Vibroengineering, Vol. 23, No. 8, pp. 1833–1844, Sep. 2021, https://doi.org/10.21595/jve.2021.22051

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2021.22051
UR  - https://doi.org/10.21595/jve.2021.22051
TI  - Development of a mathematical model of frequency controlled induction electric drive
T2  - Journal of Vibroengineering
AU  - Mustafin, Marat
AU  - Darimbaeva, Nazira
AU  - Almuratova, Nurgul
AU  - Zhauyt, Algazy
PY  - 2021
DA  - 2021/09/09
PB  - JVE International Ltd.
SP  - 1833-1844
IS  - 8
VL  - 23
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Mustafin_2021,
	doi = {10.21595/jve.2021.22051},
	url = {https://doi.org/10.21595/jve.2021.22051},
	year = 2021,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {23},
	number = {8},
	pages = {1833--1844},
	author = {Marat Mustafin and Nazira Darimbaeva and Nurgul Almuratova and Algazy Zhauyt},
	title = {Development of a mathematical model of frequency controlled induction electric drive},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]M. Mustafin, N. Darimbaeva, N. Almuratova, and A. Zhauyt, “Development of a mathematical model of frequency controlled induction electric drive,” Journal of Vibroengineering, vol. 23, no. 8, pp. 1833–1844, Sep. 2021, doi: 10.21595/jve.2021.22051.

Copy IEEE

Copied to clipboard!

Mustafin, Marat, Nazira Darimbaeva, Nurgul Almuratova, and Algazy Zhauyt. “Development of a Mathematical Model of Frequency Controlled Induction Electric Drive.” Journal of Vibroengineering 23, no. 8 (September 9, 2021): 1833–44. https://doi.org/10.21595/jve.2021.22051.

Copy Chicago

Copied to clipboard!

Development of a mathematical model of frequency controlled induction electric drive

Abstract

1. Introduction

2. Materials and methods

3. Results and discussion

4. Conclusions

References

About this article

Related Articles