Laser gyro signal filtering by combining CEEMDAN and principal component analysis

Huang, Rongrong; Yan, Lei; Liu, Jing

doi:10.21595/jve.2021.21980

Journal of Vibroengineering

Browse Journal

Submit article

Published: 03 September 2021

Check for updates

Laser gyro signal filtering by combining CEEMDAN and principal component analysis

Rongrong Huang¹

Lei Yan²

Jing Liu³

^{1, 2}College of General Quality Education, Wuchang University of Technology, Wuhan, 430223, China

³Wutaizha Primary School, Wuhan, 430000, China

Corresponding Author:

Rongrong Huang

Cite the article Download PDF

Downloads 701

WoS Core Citations 1

CrossRef Citations 3

Abstract

In order to suppress the random shift error of laser gyro and improve the practical precision of inertial navigation system, an improved gyro filtering method is proposed by combining the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and principal component analysis (PCA). Firstly, the gyro signal is decomposed by CEEMDAN, and the noise energy of each intrinsic mode function (IMF) is estimated according to the distribution model of noise energy. Then, on basis of noise energy, the principal component analysis is used to remove the noise IMF to achieve the final denoising of gyro signal. In the proposed method, CEEMD can improve the mode mixing and denoising effect of gyro signal. Moreover, PCA is used to decompose each IMF. According to the noise energy, the noise of each IMF is removed adaptively to avoid the selection of noise IMF and better retain the useful information of the signal. The proposed method is completely dependent on the characteristics of gyro signal and has good adaptability and strong denoising ability. Furthermore, the filtered effect of different methods is analyzed by overlapping Allan variance. The experimental results show that the proposed method can suppress the gyro random drift more efficiently, and the effect of removing noise is better than EMD threshold method and EMD correlation coefficient method.

1. Introduction

Laser gyroscope is a new generation of inertial measurement element. Compared with traditional mechanical gyroscope, it has many outstanding advantages and has been widely used in many fields [1]. The accuracy of the output signal of laser gyro will directly affect the alignment efficiency of inertial navigation system. Due to the influence of uncertain factors such as internal structure and external environment, the output signal of the gyro often contains a lot of random noise that seriously affects its accuracy. How to effectively reduce the random drift of the gyro and improve the output accuracy of the signal has always been a hot and difficult point in laser gyro [2]. There are currently two main methods to reduce gyro random drift [3]: one is to establish a time series model of the gyro random drift, and the Kalman filter and more are used for random drift compensation based on this; the other is to use wavelet transform and more to reduce the noise of the gyro output data. Since the gyro signal will be interfered by a variety of uncertain factors, the random drift has the characteristics of slow time-varying, nonlinear, and non-stationary, which makes it impossible to establish an accurate drift model. Therefore, a time series model is difficult to obtain the ideal compensation effect, and the current gyro signal processing mainly adopts noise reduction method [3].

To solve the problem of large random drift of MEMS gyroscope, scholars at home and abroad have adopted many methods to deal with it. For example, a digital low-pass filter was used to filter out high-frequency noise [4], but this filter needs to be designed according to experience and is not suitable for the aliasing of noise spectrum and signal spectrum. The wavelet denoising method was proposed and the wavelet coefficients were optimized through sparse redundancy representation [5], but the appropriate threshold value and wavelet basis function is difficult to be selected in the wavelet filtering. An advanced neural architecture search cyclic neural network (NAS-RNN) method was adopted [6], but the basic structure and modules used in the NAS algorithm are difficult to rely on manual design, and require a large amount of computation. The time series model with Kalman filtering method is the most commonly used method for MEMS gyroscope error compensation [7], but the filtering accuracy is low.

The empirical mode decomposition (EMD) method does not require any prior knowledge of the signal [8], nor does it need to establish an error model. The original signal can be directly decomposed into several intrinsic mode functions (IMFs) and a margin, and then the high-frequency component containing noise is removed and the low-frequency component is reconstructed to achieve the original signal. In reference [9], the dominant component of noise was screened by calculating the variance of the autocorrelation function of each IMF. The IMF component with a small variance value can be considered as the dominant component of noise. In reference [10], the correlation coefficient method was used to screen IMF. When the local minimum appeared for the first time in the correlation coefficient graph, the IMF component before the extreme point could be determined as the noise component. In reference [11], IMF components were divided into noise IMF, aliasing IMF and signal IMF according to Pearson correlation coefficient criterion, and the aliasing component was processed with good denoising effect. However, there is no definite criterion for the selection of the IMF with noise. The traditional EMD denoising method directly removes the high-frequency component dominated by noise, which will lose some useful information and lead to the deviation of reconstructed signal. In reference [12], EMD algorithm with traditional time series modeling filtering method was used to compensate the error of gyroscope. Although good filtering effect is achieved, several high-order Kalman filters are used in the filtering process, leading to poor real-time performance.

In order to overcome the influence of EMD mode mixing and noise IMF selection on denoising, a gyro signal denoising method combining CEEMDAN and principal component analysis (PCA) is proposed in this paper. This method uses CEEMD instead of EMD to achieve almost perfect signal reconstruction. It improves the mode mixing and denoising effect of gyro signal. Moreover, PCA is used to decompose each IMF, and the principal components to be retained are selected adaptively according to the noise energy, thereby removing the noise of IMF r, avoiding the screening of noise IMF, and further improving the denoising effect of gyro signal. The proposed method is completely dependent on the characteristics of gyro signal, without judging the IMF noise term and setting the threshold value. In this paper, the noise reduction experiments of laser gyro test signals are carried out, and the experimental results are analyzed by overlapping Allan variance. The results show that the proposed method can suppress the gyro random drift more effectively than the existing EMD noise reduction methods.

2. CEEMDAN and principal component analysis

2.1. CEEMDAN

The CEEMDAN algorithm can effectively solve the problem of modal aliasing caused by EMD by adding adaptive white noise in each stage of decomposition. Meanwhile, it overcomes the problem of reconstruction errors caused by EEMD through adding white noise. The CEEMDAN algorithm is shown below [13]:

Step 1: Find the first-order modal component. Add positive and negative pairs of Gaussian white noise $(- 1)^{m} ε n^{i} (t)$ to the original signal $x (t)$ in order to form a new signal $x (t) + (- 1)^{m} ε n^{i} (t)$ , and $m \in {1,2}$ . $ε$ is the amplitude. $n^{i} (t)$ is the white noise sequence added for the $i$ time and obeys the standard normal distribution, and $i$ is the number of auxiliary noises, $i = 1,2, \dots, N$ . EMD of the new signal is obtained:

1

x (t) + (- 1)^{m} ε n^{i} (t) = I M F_{1}^{i} (t) + r_{1} (t) .

At this time, $N$ first-order components $I M F_{1}^{i} (t)$ are obtained. The average value through $N$ $I M F_{1}^{i} (t)$ is found and the final weight of the first stage is obtained:

2

\bar{I M F_{1}} (t) = \frac{1}{N} \sum_{i = 1}^{N} I M F_{1}^{i} (t) .

From Eq. (1) and Eq. (2), the first-order residual component $r_{1} (t)$ is obtained:

3

r_{1} (t) = x (t) + (- 1)^{m} ε n^{i} (t) - \bar{I M F_{1}} (t) .

Step 2: Find the second-order modal component. Add positive and negative pairs of Gaussian white noise $(- 1)^{m} ε n^{i} (t)$ to the remaining component $r_{1} (t)$ to form a new signal $r_{1} (t) + (- 1)^{m} ε n^{i} (t)$ . EMD is used to decompose again:

4

r_{1} (t) + (- 1)^{m} ε n^{i} (t) = I M F_{2}^{i} (t) + r_{2} (t) .

Then, the second-order component $\bar{I M F_{2}} (t)$ is obtained by averaging $N I M F_{2}^{i} (t)$ :

5

\bar{I M F_{2}} (t) = \frac{1}{N} \sum_{i = 1}^{N} I M F_{2}^{i} (t) .

Finally, the second-order residual component is obtained:

6

r_{2} (t) = r_{1} (t) + (- 1)^{m} ε n^{i} (t) - \bar{I M F_{2}} (t) .

Step 3: Repeat step 2 until the remaining signal cannot be decomposed. Suppose that $K$ average IMF components are obtained at the end of the algorithm, the final residual signal $R (t)$ is:

R (t) = x (t) - \sum_{k = 1}^{K} \bar{I M F_{k}} (t) .

The original signal can be expressed as:

x (t) = \sum_{k = 1}^{K} \bar{I M F_{k}} (t) + R (t) .

2.2. Principal component analysis

PCA is a typical decorrelation algorithm [14], which has been widely used in dimensionality reduction, data compression, and noise removal. Suppose $X$ is a $m \times n$ matrix, i.e.:

7

X = [\begin{matrix} X_{1} \\ X_{2} \\ ⋮ \\ X_{3} \end{matrix}] = [\begin{matrix} x_{1}^{1} & x_{1}^{2} & \dots & x_{1}^{n} \\ x_{2}^{1} & x_{2}^{2} & \dots & x_{2}^{n} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ x_{3}^{1} & x_{3}^{2} & \dots & x_{m}^{n} \end{matrix}] .

Take the mean of $X_{i}$ as ${\bar{X}}_{i}$ , ${\bar{X}}_{i} = \frac{1}{n} \sum_{j = 1}^{n} x_{i}^{j}$ , and let $\bar{X} = [X_{1} - {\bar{X}}_{1}, X_{2} - {\bar{X}}_{2}, \dots, X_{m} - {\bar{X}}_{m}]^{T}$ , then the covariance matrix $Ω$ of $X$ is $Ω = \frac{1}{n} \bar{X} \cdot {\bar{X}}^{T}$ . The purpose of PCA transformation is to find an orthogonal matrix $P$ . The components in $X$ are de-correlated by the transformation $Y = P X$ , and the covariance matrix of $Y$ is diagonal matrix. Because $Ω$ is a symmetric matrix, and $Ω$ can be expressed by singular decomposition:

Ω = Φ Λ Φ^{T} = [ϕ_{1}, ϕ_{2}, \dots ϕ_{m}],

where, $Φ = [ϕ_{1}, ϕ_{2}, \dots ϕ_{m}]$ is an orthogonal matrix,}, $Λ = d i a g {λ_{1}, λ_{2}, \dots λ_{m}}$ . $λ_{1}, λ_{2}, \dots, λ_{m}$ represents the characteristic root of covariance matrix and satisfy $λ_{1} \geq λ_{2} \geq \dots \geq λ_{m}$ . $ϕ_{i}$ represents the eigenvector corresponding to $x (t)$ . If $k$ , and then the disjoint operation of each component in data $X$ can be realized by transforming $i m f_{k} = {d_{1}, d_{2}, \dots, d_{N}}$ . Components in matrix $ε (i m f_{k})$ are independent to each other.

In addition to de-correlation, another important feature of PCA is to de-noise signals by optimizing the selection of some principal components. After PCA decomposition, the noise-containing signal is mainly concentrated in the first few principal components, and the noise is distributed in each principal component to varying degrees. Therefore, as long as the first few principal components are retained for reconstruction, the noise in the signal can be significantly removed and a good de-noising effect can be achieved. That is, if let $\tilde{Y} = [Y_{1}^{T}, Y_{2}^{T}, \dots, Y_{H}^{T}, 0, \dots, 0]^{T}$ , $K < m$ , and then:

8

\tilde{X} = P^{T} \tilde{Y} = \sum_{i = 1}^{H} ϕ_{i} Y_{i},

is the result of denoising the original noise-containing signal $X$ .

3. Gyro signal denoising based on PCA and CEEMDAN

3.1. Energy composition model of gyro signal IMF

The laser gyro signal $x (t)$ is decomposed by CEEMDAN. The IMF at layer $k$ is $\bar{I M F_{k}} = {d_{1}, d_{2}, \dots, d_{N}}$ , and the energy of $\bar{I M F_{k}}$ $ε (\bar{I M F_{k}})$ is defined as [15]:

9

ε (\bar{I M F_{k}}) = \bar{I M F_{k}} \cdot {\bar{I M F_{k}}}^{T} = \sum_{n = 1}^{N} d_{n}^{2},

where, $i m f_{1}$ represents the length of $\bar{I M F_{k}}$ . For the sake of discussion, let $f_{k} = \bar{I M F_{k}}$ , assuming that:

10

f_{k} = g_{k} + V_{k},

where, $g_{k}$ represents the signal component contained in $f_{k}$ , and $V_{k}$ represents the noise component in $f_{k}$ , there are:

f_{k} - E (f_{k}) = g_{k} + V_{k} - E (g_{k} + V_{k}) = [g_{k} - E (g_{k})] + [V_{k} - E (V_{k})] .

Among them, $E ()$ indicates the expectation. According to EMD, the resolution characteristics of zero mean white noise $E (V_{k}) = 0$ , and let:

\hat{f} = f - E (f), \hat{g} = g - E (g) .

Then the above equation becomes:

11

\hat{f_{k}} = \hat{g_{k}} + V_{k} .

The energy of $\hat{f_{k}}$ , $\hat{g_{k}}$ and $V$ are $ε (\hat{f_{k}})$ , $ε (\hat{g_{k}})$ and $ε (V_{k})$ respectively. According to Eq. (9):

ε (\hat{f_{k}}) = \hat{f_{k}} \cdot {\hat{f_{k}}}^{T} = (\hat{g_{k}} + V_{k}) (\hat{g_{k}} + V_{k})^{T} = \hat{g_{k}} \cdot {\hat{g_{k}}}^{T} + \hat{g_{k}} \cdot V_{k}^{T} + V_{k} \cdot {\hat{g_{k}}}^{T} + V_{k} \cdot V_{k}^{T} .

Because signal $\hat{f_{k}}$ has nothing to do with the noise $V_{k}$ , and:

\hat{f_{k}} V_{k}^{T} = [g_{k} - E (g_{k})] [V_{k} - E (V_{k})]^{T} \approx 0, V_{k} {\hat{g_{k}}}^{T} = [V - E (V)] [\hat{g_{k}} - E (\hat{g_{k}})]^{T} \approx 0 .

So:

12

ε (\hat{f_{k}}) \approx \hat{g_{k}} {\hat{g_{k}}}^{T} + V_{k} V_{k}^{T} = ε (\hat{g_{k}}) + ε (V_{k}) .

That is, the energy of $\hat{f_{k}}$ is mainly composed of signal energy $ε (V_{k})$ and noise energy $ε (V_{k})$ . When $\hat{f_{k}}$ is denoising, if the noise with energy $ε (V_{k})$ can be removed from $\hat{f_{k}}$ , then it can be considered that the remaining part is all signal information and no longer contains noise.

The energy of $ε (V_{k})$ in $\hat{f_{k}}$ is unknown. Since the signal and noise are mixed together, and it is usually impossible to find the noise energy contained in $\hat{f_{k}}$ . However, based on the energy model of the noise signal decomposed by EMD [17, 18], the energy of $ε (V_{k})$ in $\bar{I M F_{k}}$ can be approximated. After EMD decomposition of the signal contaminated by white noise, the embedded mode function of the first layer $\bar{I M F_{1}}$ is basically composed of noise and contains only a small amount of signal information. Assuming that $\bar{I M F_{1}}$ is completely composed of noise, that is, $ε (V_{1}) = ε (\bar{I M F_{1}})$ , then the energy $ε (V_{k})$ of the noise contained in the $k$ -th IMF can be approximately obtained according to the following formula:

13

ε (V_{k}) = \frac{ε (V_{1})}{β} ρ^{k}, k \geq 2,

where, $m$ and $r$ . According to Eq. (2) and Eq. (3), the noise energy in $\hat{f_{k}} = \bar{I M F_{k}} - E (\bar{I M F_{k}})$ is the same as that in $f_{k} = \bar{I M F_{k}}$ . Therefore, the energy $ε (V_{k})$ of noise contained in $\hat{f_{k}}$ can be approximately obtained through Eq. (13). Simply let $ε (V_{1}) = ε (\bar{I M F_{1}})$ , regardless of the detailed information contained in $\bar{I M F_{1}}$ , it will lead to the excessive estimation of noise energy, which is not conducive to the preservation of signal details. If PCA is applied to $\bar{I M F_{1}}$ to extract some detailed signal information, the noise energy value of $ε (V_{1})$ in $\bar{I M F_{1}}$ can be estimated more accurately.

3.2. Principal component selection for IMF denoising at each layer

After CEEMDAN decomposition of the gyro signal, there are different degrees of noise in each IMF layer. PCA is used to further remove the noise of each IMF layer. Still make $f_{k} = \bar{I M F_{k}}$ and $\hat{f_{k}} = f_{k} - E (f_{k})$ , and let $Z = (Z_{1}, Z_{2}, \dots, Z_{N})^{T} = (f_{k})^{T}$ and $X = (X_{1}, X_{2}, \dots, X_{N})^{T} = (\hat{f_{k}})^{T}$ .

Let $m_{Z} = E (Z)$ and $m_{X} = E (X)$ , due to $X = Z - m_{Z}$ , obviously $m_{X} = 0$ , and the covariance matrix of $Z$ is obtained $C_{Z} = E {(Z - m_{Z}) (Z - m_{Z})^{T}} = E {(X - m_{X}) (X - m_{X})^{T}} = C_{X}$ .

Therefore, using PCA to denoise $f_{k}$ is equivalent to using PCA to denoise $\hat{f_{k}}$ . Let $λ_{1} \geq λ_{2} \geq \dots \geq λ_{N}$ be the characteristic value of $C_{X}$ , and $ϕ_{1}, ϕ_{2}, \dots, ϕ_{N}$ be the corresponding eigenvectors. Let $Φ = [ϕ_{1}, ϕ_{2}, \dots, ϕ_{N}]^{T}$ , i.e. $Φ$ is an orthogonal matrix. Define:

Y = (Y_{1}, Y_{2}, \dots, Y_{N})^{T} = Φ (X - m_{X}) .

According to the decomposition characteristics of PCA, the noise in $X$ is distributed in all the components in $Y_{i}$ , while the signal is mainly concentrated in the components of the first few layers. If the first $H$ eigenvectors are selected to form a new transformation matrix $Φ_{H} = [ϕ_{1}, ϕ_{2}, \dots, ϕ_{H}, 0, \dots, 0]^{T}$ , then the approximate value $\tilde{X}$ of the original signal $X$ can be obtained from $Y_{H}$ by the inverse transformation:

\tilde{X} - m_{X} = Φ_{H}^{T} Y_{H} = \sum_{i = 1}^{H} ϕ_{i} Y_{i} .

Therefore, $\tilde{X} = \sum_{i = 1}^{H} ϕ_{i} Y_{i} + m_{X}$ is the signal de-noised by $\hat{f_{k}}$ , and:

14

Δ X = X - \tilde{X} = \sum_{i = H + 1}^{N} ϕ_{i} Y_{i},

is equivalent to the noise removed from $\hat{f_{k}}$ . When PCA is used to remove the noise in $i m f_{k}$ , an appropriate number of principal components is selected for reconstruction. Usually, according to the cumulative contribution rate of the first $H$ principal components $r = (\sum_{i = 1}^{H} λ_{i} / \sum_{i = 1}^{N} λ_{i})$ to determine the principal components retained. However, the selection of principal component is not simple: if the cumulative contribution rate r is too high, there will be a lot of residual noise, resulting in incompletely removal of noise; If the cumulative contribution rate r is too small, more signal details will be lost. Moreover, the intensity of noise contained in each IMF layer is different. Therefore, in the denoising process of $\bar{I M F_{k}}$ , the cumulative contribution rate $r$ cannot be set to a fixed value. Based on the distribution characteristics of noise energy in $\bar{I M F_{k}}$ , this paper adaptively determines the value of the cumulative contribution rate r in denoising.

3.2.1. Principal component selection of $\bar{I M F_{1}}$

From CEEMDAN's decomposition characteristics of noise signals [16], it can be seen that IMF is basically composed of noise and only contains a small amount of signal details. After PCA decomposition, the signal is basically only concentrated in the first principal component. Therefore, when using PCA to de-noise $\hat{f_{1}}$ , only the first principal component is retained for reconstruction. That is, make $X = \hat{f_{1}},$ and $X$ de-noised by PCA is the signal $\tilde{X} = (ϕ_{1}, 0,0, \dots, 0) Y = ϕ_{1} Y_{1}$ . At this point, the noise removed from $X$ is:

15

Δ X = X - \tilde{X} = \sum_{i = 2}^{N} ϕ_{i} Y_{i} .

Therefore, the energy of noise $ε (V_{1}) ε (Δ X)$ contained in $\hat{f_{1}}$ can be obtained. According to the noise energy distribution in the EMD model Eq. (13) and $ε (V_{1})$ , $\hat{f_{k}}$ value contained in the noise energy is calculated.

3.2.2. Principal component selection of $\bar{I M F_{k}} (k \geq 2)$

The following discusses the principal component selection method of $\hat{f_{k}} = \bar{I M F_{k}} - E (\bar{I M F_{k}})$ at $k \geq 2$ . From Eq. (12), the energy of $\hat{f_{k}}$ is mainly composed of ideal signal energy and noise energy. If appropriate $H$ is selected during the PCA reconstruction, the energy of noise $Δ X$ deleted in Eq. (14) is the same as that of $V_{k}$ contained in $\hat{f_{k}}$ . That is, $H$ is selected, let:

ε (Δ X) = ε (V_{k}) .

It is considered that the noise has been completely removed, and the remaining principal component is the ideal signal $\hat{g_{k}}$ without noise. In order to facilitate the calculation and reduce the error, the above Formula is modified to:

16

\frac{ε (Δ X)}{ε (X)} = \frac{ε (V_{k})}{ε (X)} .

It can be seen from Eq. (14) that the energy of the deleted noise $Δ X$ is:

ε (Δ X) = (Δ X)^{T} Δ X = \sum_{i = H + 1}^{N} \sum_{j = H + 1}^{N} Y_{i}^{T} ϕ_{i}^{T} ϕ_{j} Y_{j} = \sum_{i = H + 1}^{N} Y_{i}^{2} = \sum_{i = H + 1}^{N} Y_{i} Y_{i}^{T} .

Since $Y_{i} = ϕ_{i}^{T} (X - m_{X})$ , and:

ε (Δ X) = \sum_{i = H + 1}^{N} ϕ_{i}^{T} (X - m_{X}) (X - m_{X})^{T} ϕ_{i} = N \sum_{i = H + 1}^{N} ϕ_{i}^{T} [\frac{1}{N} (X - m_{X}) (X - m_{X})^{T}] ϕ_{i}

= N \sum_{i = H + 1}^{N} ϕ_{i}^{T} E [(X - m_{X}) (X - m_{X})^{T}] ϕ_{i} = N \sum_{i = H + 1}^{N} ϕ_{i}^{T} C_{X} ϕ_{i} = N \sum_{i = H + 1}^{N} ϕ_{i}^{T} λ_{i} ϕ_{i}

= N \sum_{i = H + 1}^{N} λ_{i} .

Due to $X = \sum_{i = 1}^{N} ϕ_{i} Y_{i} + m_{X}$ and $m_{X} = 0$ , and the energy of signal $X$ is:

ε (X) = X^{T} X = (\sum_{i = 1}^{N} ϕ_{i} Y_{i}) (\sum_{j = 1}^{N} ϕ_{j} Y_{j}) = \sum_{i = 1}^{N} \sum_{j = 1}^{N} Y_{i}^{T} ϕ_{i}^{T} ϕ_{j} Y_{j} = \sum_{i = 1}^{N} Y_{i} Y_{i}^{T}

= N \sum_{i = 1}^{N} ϕ_{i}^{T} \frac{1}{N} (X - m_{X}) (X - m_{X})^{T} ϕ_{i}^{} = N \sum_{i = 1}^{N} ϕ_{i}^{T} E [(X - m_{X}) (X - m_{X})^{T}] ϕ_{i}

= N \sum_{i = 1}^{N} ϕ_{i}^{T} C_{X} ϕ_{i}^{} = N \sum_{i = 1}^{N} λ_{i} .

When using PCA to de-noise $\hat{f_{k}}$ , if the first $H$ principal components are selected for reconstruction, the ratio of the energy of the deleted noise $Δ X$ to that of the original signal $X$ is $\frac{ε (Δ X)}{ε (X)} = \frac{\sum_{i = H + 1}^{N} λ_{i}}{\sum_{i = 1}^{N} λ_{i}}$ . It can be seen from Eq. (16) that in order to make the energy of deleted noise equal to that of the noise contained in $\tilde{f} = f - \bar{f}$ , an appropriate $H$ should be selected as that $\frac{\sum_{i = H + 1}^{N} λ_{i}}{\sum_{i = 1}^{N} λ_{i}} = \frac{ε (V_{k})}{ε (X)}$ . It can be considered that all noises in $\tilde{f} = f - \bar{f}$ has been removed, and the remaining part is all composed of signal information without noise. $\tilde{f} (n)$ can be calculated by Eq. (7) and noise energy model Eq. (13), and $ε (X)$ can be calculated directly. When choose $H$ , it is hard to be sure that $\frac{\sum_{i = H + 1}^{N} λ_{i}}{\sum_{i = 1}^{N} λ_{i}} = \frac{ε (V_{k})}{ε (X)}$ is true.

In this paper, the value of $H$ is selected according to the following method: if there is ${ϕ_{i}}$ , Eq. (17) is established, and let $r_{N}$ :

17

M = m_{0} \leq \frac{ε (V_{k})}{ε (X)} \leq i m f_{k}, (k = 1,2 \dots, N) .

3.3. De-noising steps of gyro signal based on CEEMDAN and PCA

The laser gyro signal denoising algorithm based on CEEMDAN and PCA proposed in this paper are as follows:

Conduct CEEMDAN on the gyro signal $x (t)$ , and set its intrinsic modal function as $\bar{I M F_{k}}$ $(k = 1,2 \dots, K)$ , and the remainder as $R (t)$ ;

Let $ε (V_{1}) = ε (\bar{I M F_{1}})$ , and calculate the energy $ε (W_{k})$ $(k \geq 2)$ of the noise contained in $\bar{I M F_{k}}$ according to Eq. (13).

Let $\hat{f_{k}} = \bar{I M F_{k}} - E (\bar{I M F_{k}})$ , $k = 1,2, \dots, K$ .

PCA decomposition is performed on $\hat{f_{k}}$ . Through Eq. (17), the principal component $H$ retained in the denoising of feature space is calculated. According to $\tilde{X} = \sum_{i = 1}^{H} ϕ_{i} Y_{i} + m_{X}$ , the denoising result is found in the feature space, and the original image ${\hat{f_{k}}}^{'}$ is found through iteration.

The de-noising result of $\bar{I M F_{k}}$ is ${\bar{I M F_{k}}}^{'} = {\hat{f_{k}}}^{'} + E (\bar{I M F_{k}})$ . Accumulate and reconstruct ${\bar{I M F_{k}}}^{'}$ $(k = 1,2, \dots, K)$ to get the de-noised gyro signal $x' (t) = \sum_{k = 1}^{N} {\bar{I M F_{k}}}^{'} (t) + R (t)$ .

4. Experimental analysis

4.1. Experiment 1

The experimental data in this article comes from the drift test of a laser gyro under a static base at normal temperature (20 °C) (the nominal gyro drift is 1 °/h). The sampling interval is 1 s, and the output signal of 2000 epochs on the $x$ -axis is taken for experimental analysis (similar to the $y$ and $z$ -axes). The experimental data is shown in Fig. 1. In order to compare the denoising effect, the gyro signal is de-noised by the EMD threshold method [12], the EMD correlation coefficient method [9] and the proposed method in this paper. In the denoising of EMD threshold method and EMD correlation coefficient method, the number of decomposition layers is 9. After the experimental signal is decomposed by CEEMDAN under the proposed method, 10 IMF components and one remainder are obtained.

4.1.1. Direct comparison of denoising gyro signals

The laser gyro drift signal is de-noised by the EMD threshold method, the EMD correlation coefficient method and the method, and the results are shown in Fig. 2, Fig. 3, and Fig. 4 respectively. Compared with the signals de-noised by the EMD threshold method and the EMD correlation coefficient method, the signal de-noised by the proposed method is smoother. Calculate the mean value and variance of the original signal and the denoising signal respectively, and the results are shown in Table 1. It can be seen that the mean values of the three methods after denoising are basically the same. The variance of the proposed method after denoising is small, which shows that the random noise in the gyro drift data is better eliminated.

Table 1Comparison table of mean and variance

	Original signal	EMD threshold method	EMD correlation coefficient method	Proposed method
Mean (pulse/s)	2.4733	2.3384	2.2429	2.0491
Variance (pulse/s)²	104.8087	3.3047	2.7739	1.5620

Fig. 1The original signal of the laser gyroscope

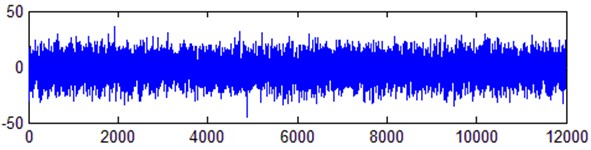
Fig. 2EMD threshold method denoising

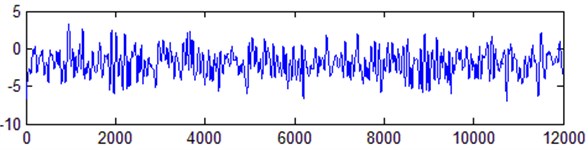
Fig. 3EMD correlation coefficient method denoising

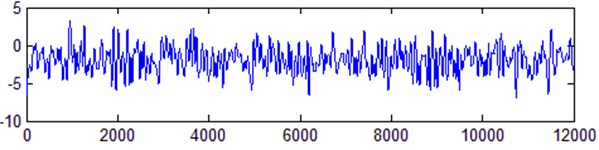
Fig. 4Denoising method of the proposed method

4.1.2. Comparison of overlapping Allan variance of denoising gyro signal

In order to further analyze the denoising effect of the method in this paper on the gyro signal, the overlapped Allan variance is used to compare and analyze the denoising results of the three methods [17]. Overlapping Allan variance is an improvement to ordinary Allan variance. It has a larger confidence interval than ordinary Allan variance analysis and is suitable for error analysis of non-stationary random gyro signals. Let the overlapped Allan standard deviation of the signal be $σ (τ) τ = n τ_{0}$ , and $τ = n τ_{0}$ be the sampling interval. The double logarithmic curve of $σ (τ) ~ τ$ can describe the different random error components of the gyro signal. The original signal is obtained by the overlapping Allan analysis method, and the coefficients of the five source errors of the signal after the three methods are de-noised, including: quantization noise ( $Q$ ), angle random walk ( $N$ ), bias instability ( $B$ ), rate random walk ( $K$ ) and rate ramp ( $R$ ). The results are shown in Table 2.

It can be seen from Table 2 that after the filtering processing of the three noise reduction algorithms, the error coefficients is reduced, indicating that the three methods have a certain denoising effect on the gyro signal. Compared with the EMD threshold method and the EMD correlation coefficient method, the various indicators of the signal after noise reduction in this method are low. It indicates that the gyro signal after the EMD threshold method and the EMD correlation coefficient method still contains a certain degree of error components. The method in this paper further weakens the various error components of the gyro signal. It can also be seen from Table 2 that quantization noise is the main factor causing the random errors in the gyro signal. After noise reduction by EMD threshold method, EMD correlation coefficient method and this proposed method, the quantization noise error coefficient of the signal is reduced to the original 13.82 %, 11.14 % and 6.46 %, respectively.

Table 2Comparison of noise error coefficient before and after denoising

Algorithm	$Q$ (μrad)	$N$ / (°/h^-1/2)	$B$ (°/h)	$K$ / (°/h^3/2)	$R$ (°/h²)	$Q$ noise reduction front-to-rear ratio (%)
Original signal	6.3632	0.1372	0.4879	2.3392	6.2326e-04	100
EMD threshold method	0.8792	0.0287	0.2190	0.4068	1.2144e-04	13.82
EMD correlation coefficient method	0.7091	0.0194	0.1613	0.3089	4.2933e-05	11.14
Proposed method	0.4113	0.0086	0.0924	0.1322	1.2977e-05	6.46

4.2. Experiment 2

In this experiment, the low cost MPU-6050 gyroscope is studied. At room temperature, the calibrated MEMS inertial sensor is fixed on the horizontal test bench through a clamp, and the sampling frequency is set to 100 Hz. After power-on, the data is collected continuously for 30 s after preheating for 0.5 h. The $Y$ axis sampling data of the gyroscope is used as the original output data of the gyroscope. After calculation, the original signal of gyroscope random drift error is shown in Fig. 5. The de-noised results of EMD threshold method, EMD correlation coefficient method and the proposed method are shown in Fig. 5. To further evaluate the effect of various denoising methods, root mean square error (MSE) and signal-to-noise ratio (SNR) are used to measure the denoising effect:

18

M S E = \sqrt{\sum_{i = 1}^{N} {[f (i) - f^{'} (i)]}^{2}},

19

S N R = 10 \times \lg (\frac{\sum_{i = 1}^{N} f^{2} (i)}{\sum_{i = 1}^{N} {[f (i) - f^{'} (i)]}^{2}}),

where, $f (i)$ is the original signal, and $f' (i)$ is the de-noised signal. The larger the SNR is, the smaller the root mean square error is, and the better the denoising effect will be.

MSE and SNR are calculated respectively as shown in Table 3. The EMD Threshold Method denoising method directly removes the coefficients that are smaller than the threshold value in each IMF layer, resulting in partial information missing. The EMD correlation coefficient method directly removes the modal units with small correlation coefficients, which also leads to the loss of gyro signal. While using the proposed method to de-noise, the signal waveform is well preserved. Compared with the EMD threshold method, the MSE of the proposed method is reduced by 12 % and the SNR is improved by 13 %. Compared with the EMD correlation coefficient method, the MSE of the proposed method is reduced by 12 % and the SNR is increased by 13 %.

Table 3Evaluation of gyroscope signal denoising effect

Method	MSE	SNR
Original signal	0.1065	15.3005
EMD threshold method	0.0914	22.3445
EMD correlation coefficient method	0.0943	23.7260
The proposed method	0.0827	25.3522

Experiment 1 and experiment 2 are carried out by Windows10 system, 2.90G Hz i5 processor of CPU, 16.0GB memory, and the software uses the Matlab2019A. In the experiment, the number of decomposition layers of CEEMDAN is set as 9. In experiment 1, the average running time of the three denoising methods is about 0.60227 s, 0.62782 s and 1.06885 s, respectively. In experiment 2, the average running time of them is about 0.38944 s, 0.40896 s and 0.71315 s, respectively.

Fig. 5Denoisied results of three methods in Experiment 2

a) Original signal

b) EMD threshold method denoising

c) EMD correlation coefficient method denoising

d) Denoising method of the proposed method

Through comparative analysis, it can be seen that in the proposed method, due to the need of multiple iterative decomposition for CEEMDAN and the use of PCA to remove the noise in each IMF, the running time is increased to a certain extent compared with the EMD Threshold Method and the EMD Correlation Coefficient Method. In the Matlab2019A environment, the average time of the implementation phase of the proposed method is about 0.891 s. It can be seen that the proposed method can quickly obtain the denoising results of gyro signals in practical applications. If the algorithm is written into the hardware by $C$ or other compiled languages, the running speed will be further improved. Therefore, the proposed method in this paper can meet the requirements in terms of real-time performance under certain conditions.

5. Conclusion

1) In order to overcome the shortcomings of the existing EMD gyro signal denoising algorithm, this paper combines CEEMDAN and PCA to propose an improved gyro signal denoising method.

2) According to the noise energy contained in IMF in each layer of gyro signal, the principal components of IMF that should be retained after PCA decomposition is adaptively selected to realize the denoising of gyro signal.

3) In the denoising process, the proposed method can adaptively calculate the model parameters according to the characteristics of gyro signal. Therefore, the denoising process is only related to the characteristics of gyro signal and does not require cumbersome parameters and threshold adjustments.

4) The noise reduction of the measured gyro random drift signal is carried out, and the noise reduction effects of different denoising methods are compared and analyzed by using direct comparison method and overlapping Allan variance method.

5) The experimental results show that compared with EMD threshold denoising method and EMD correlation coefficient denoising method, the noise reduction effect of the proposed method improves to a certain extent. It can remove noise, reduce the error components of gyro signal, and improve the accuracy of the inertial guidance solution more effectively. Moreover, the proposed method in this paper has better stability and adaptability in the processing of gyro signals.

References

Y. V. Filatov, P. A. Pavlov, A. A. Velikoseltsev, and K. U. Schreiber, “Precision angle measurement systems on the basis of ring laser gyro,” Sensors, Vol. 20, No. 23, p. 6930, Dec. 2020, https://doi.org/10.3390/s20236930

Publisher
M. Wang, X. Dong, C. Qin, and J. Liu, “Adaptive H∞ Kalman filter based random drift modeling and compensation method for ring laser gyroscope,” Measurement, Vol. 167, p. 108170, Jan. 2021, https://doi.org/10.1016/j.measurement.2020.108170

Publisher
K. Liu et al., “Noise analysis of a passive resonant laser gyroscope,” Sensors, Vol. 20, No. 18, p. 5369, Sep. 2020, https://doi.org/10.3390/s20185369

Publisher
F. S. Tian, “Research on navigation solution of multi-rotor UAV based on multiple sensors,” Harbin Institute of Technology, 2017.

Search CrossRef
J. Song, Z. Shi, B. Du, L. Han, H. Wang, and Z. Wang, “MEMS gyroscope wavelet de-noising method based on redundancy and sparse representation,” Microelectronic Engineering, Vol. 217, p. 111112, Sep. 2019, https://doi.org/10.1016/j.mee.2019.111112

Publisher
Z. Zhu, Y. Bo, and C. Jiang, “A MEMS gyroscope noise suppressing method using neural architecture search neural network,” Mathematical Problems in Engineering, Vol. 2019, pp. 1–9, Nov. 2019, https://doi.org/10.1155/2019/5491243

Publisher
Liu X. B., Chen G. W., Wang D., and Wang D. F., “Analysis and compensation of drift and noise in MEMS Gyroscop,” Chinese Journal of Sensors and Actuators, Vol. 31, No. 3, p. 368, 2018.

Search CrossRef
N. E. Huang et al., “The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis,” Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, Vol. 454, No. 1971, pp. 903–995, Mar. 1998, https://doi.org/10.1098/rspa.1998.0193

Publisher
Liu M., Liu J. H., Chen J. H., and Peng F. C., “MEMS Gyroscope noise reduction method based on improved EMD,” Chinese Journal of Sensors and Actuators, Vol. 33, No. 5, pp. 705–710, 2020.

Search CrossRef
He J. N., Zhong Y., and Li X. F., “Multi-scale prediction of MEMS gyroscope random drift based on EMD-SVR,” Journal of Measurement Science and Instrumentation, Vol. 11, No. 3, pp. 290–296, 2020.

Search CrossRef
Liu Wenta, Liu Jieyu, and Shen Qiang, “Integrated modeling and filtering of fiber optic gyroscope’s random errors,” Opto-Electronic Engineering, Vol. 45, No. 10, p. 180082, 2018.

Search CrossRef
Yang J. H. et al., “A modeling method for random errors of micromechanical gyroscope based on the improved EMD,” Chinese Journal of Scientific Instrument, Vol. 40, No. 12, pp. 196–204, 2019.

Search CrossRef
M. E. Torres, M. A. Colominas, G. Schlotthauer, and P. Flandrin, “A complete ensemble empirical mode decomposition with adaptive noise,” in ICASSP 2011 – 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 4144–4147, May 2011, https://doi.org/10.1109/icassp.2011.5947265

Publisher
Lei Zhang, R. Lukac, Xiaolin Wu, and D. Zhang, “PCA-based spatially adaptive denoising of CFA images for single-sensor digital cameras,” IEEE Transactions on Image Processing, Vol. 18, No. 4, pp. 797–812, Apr. 2009, https://doi.org/10.1109/tip.2008.2011384

Publisher
P. Flandrin, G. Rilling, and P. Goncalves, “Empirical mode decomposition as a filter bank,” IEEE Signal Processing Letters, Vol. 11, No. 2, pp. 112–114, Feb. 2004, https://doi.org/10.1109/lsp.2003.821662

Publisher
X.-D. Niu, L.-R. Lu, J. Wang, X.-C. Han, X. Li, and L.-M. Wang, “An improved empirical mode decomposition based on local integral mean and its application in signal processing,” Mathematical Problems in Engineering, Vol. 2021, pp. 1–30, Feb. 2021, https://doi.org/10.1155/2021/8891217

Publisher
K. Maciuk, J. Kudrys, M. Bagherbandi, and I. V. Bezmenov, “A new method for quantitative and qualitative representation of the noises type in Allan (and related) variances,” Earth, Planets and Space, Vol. 72, No. 1, p. 186, Dec. 2020, https://doi.org/10.1186/s40623-020-01328-6

Publisher

Cited by

2024 IEEE International Conference on Contemporary Computing and Communications (InC4)

K. Sathvik Kamath | M. Lekshmi Nair | Rinu Chacko | P. E Ameenudeen

(2024)

A spatiotemporal model for PM2 .5 prediction based on the K‐Core idea and label distribution

Yizhun Zhang | Qisheng Yan

(2023)

2023 5th International Academic Exchange Conference on Science and Technology Innovation (IAECST)

Guorui Luan | Yihu Xu

(2023)

About this article

Received

07 April 2021

Accepted

06 August 2021

Published

03 September 2021

SUBJECTS

Dynamics and oscillations in electrical and electronics engineering

DOI

https://doi.org/10.21595/jve.2021.21980

Keywords

Gyro random drift

CEEMDAN

principal component analysis

filtering

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 10 31

Research on tool condition monitoring (TCM) using a novel unsupervised deep neural network (DNN)

Jingjing Gao, Jing Liu, Xinli Yu

Research article

2019 11 15

Novel complete ensemble EMD with adaptive noise-based hybrid filtering for rolling bearing fault diagnosis

Xiaojun Song, Hongwei Sun, Liwei Zhan

Research article

2018 09 30

Feature extraction for rolling element bearing weak fault based on MOMEDA and ICEEMDAN

Lei Zhao, Yongxiang Zhang, Danchen Zhu

Research article

2017 12 31

EEMD-Based cICA method for single-channel signal separation and fault feature extraction of gearbox

Junfa Leng, Shuangxi Jing, Chenxu Luo, Zhiyang Wang

R. Huang, L. Yan, and J. Liu, “Laser gyro signal filtering by combining CEEMDAN and principal component analysis,” Journal of Vibroengineering, Vol. 23, No. 8, pp. 1820–1832, Sep. 2021, https://doi.org/10.21595/jve.2021.21980

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2021.21980
UR  - https://doi.org/10.21595/jve.2021.21980
TI  - Laser gyro signal filtering by combining CEEMDAN and principal component analysis
T2  - Journal of Vibroengineering
AU  - Huang, Rongrong
AU  - Yan, Lei
AU  - Liu, Jing
PY  - 2021
DA  - 2021/09/03
PB  - JVE International Ltd.
SP  - 1820-1832
IS  - 8
VL  - 23
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Huang_2021,
	doi = {10.21595/jve.2021.21980},
	url = {https://doi.org/10.21595/jve.2021.21980},
	year = 2021,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {23},
	number = {8},
	pages = {1820--1832},
	author = {Rongrong Huang and Lei Yan and Jing Liu},
	title = {Laser gyro signal filtering by combining {CEEMDAN} and principal component analysis},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]R. Huang, L. Yan, and J. Liu, “Laser gyro signal filtering by combining CEEMDAN and principal component analysis,” Journal of Vibroengineering, vol. 23, no. 8, pp. 1820–1832, Sep. 2021, doi: 10.21595/jve.2021.21980.

Copy IEEE

Copied to clipboard!

Huang, Rongrong, Lei Yan, and Jing Liu. “Laser Gyro Signal Filtering by Combining CEEMDAN and Principal Component Analysis.” Journal of Vibroengineering 23, no. 8 (September 3, 2021): 1820–32. https://doi.org/10.21595/jve.2021.21980.

Copy Chicago

Copied to clipboard!

Laser gyro signal filtering by combining CEEMDAN and principal component analysis

Abstract

1. Introduction

2. CEEMDAN and principal component analysis

2.1. CEEMDAN

2.2. Principal component analysis

3. Gyro signal denoising based on PCA and CEEMDAN

3.1. Energy composition model of gyro signal IMF

3.2. Principal component selection for IMF denoising at each layer

3.2.1. Principal component selection of IMF1¯

3.2.2. Principal component selection of IMFk¯ (k≥2)

3.3. De-noising steps of gyro signal based on CEEMDAN and PCA

4. Experimental analysis

4.1. Experiment 1

4.1.1. Direct comparison of denoising gyro signals

4.1.2. Comparison of overlapping Allan variance of denoising gyro signal

4.2. Experiment 2

5. Conclusion

References

Cited by

About this article

Related Articles

3.2.1. Principal component selection of $\bar{I M F_{1}}$

3.2.2. Principal component selection of $\bar{I M F_{k}} (k \geq 2)$