The fuzzy model of ships collision risk rating in a heavy traffic zone

Sedov, Viktor A.; Sedova, Nelly A.; Glushkov, Sergey V.

Vibroengineering Procedia

Browse Procedia

Published: 07 October 2016

Check for updates

The fuzzy model of ships collision risk rating in a heavy traffic zone

Viktor A. Sedov¹

Nelly A. Sedova²

Sergey V. Glushkov³

^{1, 2, 3}Maritime State University named after G. I. Nevelskoy, Vladivostok, Russian Federation

Corresponding Author:

Viktor A. Sedov

Cite the article Download PDF

Downloads 1273

Abstract

The fuzzy model to determine the risk collision rating of ships in a heavy traffic zone is proposed. Fuzzy system includes four inputs and one output linguistic variables, describing collision risk rating. The fuzzy sets corresponding to the term of these linguistic variables and their graphical view is represented. The product base contains 400 fuzzy rules, making by a maneuverable plane-table.

1. Introduction

Navigation today is characterized by, on the one hand, requirements for safe operation of water transportation, and, on the other hand, by the lack of reduction in the number of dangerous incidents and accidents. Automated methods have been developed to support the decision makers (DMP) on board, including systems using the methods of cognitive analysis, probabilistic methods [1] and / or the theory of fuzzy sets [2-4]. Such automated systems [5] are designed, for instance, for the evaluation of a particular situation related to navigation and/or calculating the risk collision rating (risk or probability of danger area) with objects and/or other vessels [6]. These are in no way a substitute for the requirement to maintain “proper sight and hearing”, regulated by rule 8 of the International Regulations for Preventing Collisions at Sea (COLREG) [7]; instead they notify the decision makers about potential dangers in order to prevent accidents. In this paper, we propose a model using the theory of fuzzy sets to determine the risk collision rating of ships in a heavy traffic zone [7, 8]. In this model the maneuverable plane-table was used for forming fuzzy base products, and the well-known Mamdani algorithm was used for fuzzy inference algorithm [9].

2. Description of the logical-linguistic model for assessing the risk rate of ship collision

The logical-linguistic model [10] consists of four input linguistic variables (LV) [11]: bearing; the course of the operator vessel (our vessel); the course of the target vessel (TV), i.e. the vessel which should the operator vessel (OV) should miss; mutual velocity, i.e., the ratio of TV speed to OV speed, and one output LV – the risk collision rating. The first three inputs of the LV are characterized by a universal set [0; 360]°, the fourth input of the LV is a universal set [0; 2] (and the right-hand limit of the set may be increased). The output LV is characterized by the set [0, 1]; in this case the closer the LV is to one, the greater the risk of collision of TV and OV. The output LV can be replaced by any other segment that is convenient for the DMP, but it is necessary to pre-normalize.

The basic term-set of the first LV input “bearing” (B) includes the following five terms of basic term-sets: the eastern bearing (EB), the western bearing (WB), the northern left bearing (NLB), the northern right bearing (NRB) and the southern bearing (SB).

Membership functions for the first input LV term “bearing” have a trapezoidal shape with parameters for EB function: $a =$ 60, $b =$ 70, $c =$ 110, $d =$ 120; for WB function: $a =$ 240, $b =$ 250, $c =$ 290, $d =$ 300; for NLB function: $a =$ 300, $b =$ 310, $c =$ 350, $d =$ 360; for NRB functions: $a =$ 0, $b =$ 10, $c =$ 50, $d =$ 60; and for SB function they are: $a =$ 120, $b =$ 130, $c =$ 230, $d =$ 240.

The second LV input “the course of operator vessel” (COS) is a basic term-set consisting of the following elements: course left to the north (NL), course right to the north (NR), course to the east (E), to the south (S) and to the west (W). Membership functions for the second input LV terms are trapezoidal with following parameters for function NR: $a =$ 0, $b =$ 10, $c =$ 50, $d =$ 60; for NL: $a =$ 300, $b =$ 310, $c =$ 350, $d =$ 360; for E: $a =$ 60, $b =$ 70, $c =$ 110, $d =$ 120; for S: $a =$ 120, $b =$ 130, $c =$ 230, $d =$ 240 and for W: $a =$ 240, $b =$ 250, $c =$ 290, $d =$ 300.

The third LV input “the course of target vessel” (CTV) is a basic term-set including the following elements: course left to the north (TNL), course right to the north (TNR), course to the east (TE), course to the south (TS) and course to the west (TW). Membership functions for the terms of the third input LV has a trapezoidal shape with parameters for TNL function: $a =$ 300, $b =$ 310, $c =$ 350, $d =$ 360; for TNR function: $a =$ 0, $b =$ 10, $c =$ 50, $d =$ 60; for TE function: $a =$ 60, $b =$ 70, $c =$ 110, $d =$ 120; for TS function: $a =$ 120, $b =$ 130, $c =$ 230, $d =$ 240 and for the TW function: $a =$ 240, $b =$ 250, $c =$ 290, $d =$ 300.

Analytical representation of the LV input terms “bearing”, “CTV” and “COS” is shown below:

μ_{N R B; N R; T N R} (x) = \{\begin{array}{l} 0, x \leq 0, \\ \frac{x}{10}, 0 \leq x \leq 10, \\ 1, 10 \leq x \leq 50, \\ \frac{60 - x}{10}, 50 \leq x \leq 60, \\ 0, 60 \leq x, \end{array} μ_{E B; E; T E} (x) = \{\begin{array}{l} 0, x \leq 60, \\ \frac{x - 60}{10}, 60 \leq x \leq 70, \\ 1, 70 \leq x \leq 110, \\ \frac{120 - x}{10}, 110 \leq x \leq 120, \\ 0, 120 \leq x, \end{array}

μ_{S B; S; T S} (x) = \{\begin{array}{l} 0, x \leq 120, \\ \frac{x - 120}{10}, 120 \leq x \leq 130, \\ 1, 130 \leq x \leq 230, \\ \frac{240 - x}{10}, 230 \leq x \leq 240, \\ 0, 240 \leq x, \end{array} μ_{W B; W; T W} (x) = \{\begin{array}{l} 0, x \leq 240, \\ \frac{x - 240}{10}, 240 \leq x \leq 250, \\ 1, 250 \leq x \leq 290, \\ \frac{300 - x}{10}, 290 \leq x \leq 300, \\ 0, 300 \leq x, \end{array}

μ_{N L B; N L; T N L} (x) = \{\begin{array}{l} 0, x \leq 300, \\ \frac{x - 300}{10}, 330 \leq x \leq 310, \\ 1, 310 \leq x \leq 350, \\ \frac{360 - x}{10}, 350 \leq x \leq 360, \\ 0, 360 \leq x . \end{array}

The fourth LV input “relative speed” (RS) has the following terms of basic term-sets: standing target (ST), less than one (L1), equal to one (E1), more than one (M1). Membership functions for the fourth LV input terms are triangular and S-shaped functions with parameters for ST: $a =$ 0, $b =$ 0, $c =$ 0,13; for L1 function: $a =$ 0,13, $b =$ 0,5, $c =$ 0,87; for E1 function: $a =$ 0,87, $b =$ 1, $c =$ 1,13 and for M1 function: $a =$ 1,13, $b =$ 1,5. ST term of fourth input LV RS is the membership function, analytic form which:

μ_{S T} (x) = \{\begin{array}{l} \frac{0,13 - x}{0,13}, 0 < x < 0,13, \\ 0, 0,13 \leq x . \end{array}

The L1 and E1 terms of the fourth LV input RS have the following membership functions respectively:

μ_{L 1} (x) = \{\begin{array}{l} 0, x \leq 0,13, \\ \frac{x - 0,13}{0,37}, 0,13 \leq x \leq 0,5, \\ \frac{0,87 - x}{0,37}, 0,5 \leq x \leq 0,87, \\ 0, 0,87 \leq x . \end{array} μ_{E 1} (x) = \{\begin{array}{l} 0, x \leq 0,87, \\ \frac{x - 0,87}{0,13}, 0,87 \leq x \leq 1, \\ \frac{1,13 - x}{0,13}, 1 \leq x \leq 1,13, \\ 0, 1,13 \leq x . \end{array}

M1 therm of the fourth LV input RS is the membership function with analytic form:

μ_{M 1} (x) = \{\begin{array}{l} 0, x \leq 1,13, \\ \frac{x - 1,13}{0,37}, 1,13 < x < 1,5, \\ 1, 1,5 \leq x . \end{array}

The output LV “Danger of collision” (DofC) has a triangular membership function with the parameters for the term “low danger of collision» (LDC): $a =$ 0, $b =$ 0, $c =$ 0,4; for the term “medium danger of collision” (MDC): $a =$ 0,1, $b =$ 0,5, $c =$ 0,9 and for the term “high danger of collision” (HDS): $a =$ 0,6, $b =$ 1, $c =$ 1.

The LDC term of LV output DofC has a membership function, which is an analytical view:

μ_{L D C} (x) = \{\begin{array}{l} \frac{0,4 - x}{0,4}, 0 < x < 0,4, \\ 0, 0,4 \leq x . \end{array}

The MDC term of output LV DofC has a following membership function:

μ_{M D C} (x) = \{\begin{array}{l} 0, x \leq 0,1, \\ \frac{x - 0,1}{0,4}, 0,1 \leq x \leq 0,5, \\ \frac{0,9 - x}{0,4}, 0,5 \leq x \leq 0,9, \\ 0, 0,9 \leq x . \end{array}

The HDC term of output LV DofC has a membership function with analytical form:

μ_{L D C} (x) = \{\begin{array}{l} \frac{x - 0,6}{0,4}, 0,6 < x < 1, \\ 1, 1 \leq x . \end{array}

3. The rule base of fuzzy productions

The general scheme of the logical-linguistic model for determining the risk of collision rate of ships in a heavy traffic zone is shown on Fig. 1.

A maneuvering plane-table was used for forming the base of fuzzy rules products (FRP). For each rule of the fuzzy production the following procedure was carried out.

Step 1. A list of various situations using an exhaustive search with certain intervals for each input LV term-set was determined; this enabled the conditions for each FRP to be determined.

Step 2. Fixing the terms constituting each FPR for input into the rule base of fuzzy products.

Step 3. The disposition of each situation formed in step 1 was laid out on a maneuvering plane-table.

Step 4. Getting a numerical equivalent in the interval [0, 1] of the rating of risk collision degree taking into account step 3, COLREG rules [7], COLREG commentaries and “good seamanship” recommendations.

Step 5. Fixed the terms for input into the rule base of the FPR based on the data about risk collision degree obtained in step 4.

Thus, the FPR base, consisting of 400 rules, was formed.

Fig. 1The general scheme of the logical-linguistic model

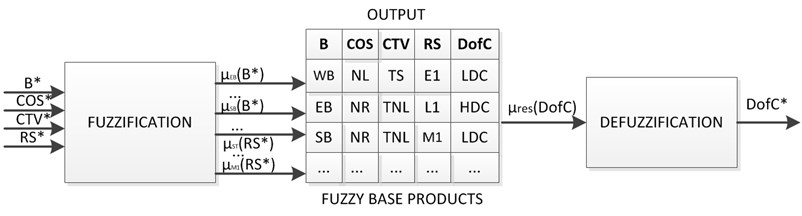
The logical-linguistic model for determining the risk collision rating of ships in a heavy traffic zone was implemented using Matlab software [6]. A simulation of the logical-linguistic model was tested on 400 test cases. The following was calculated to evaluate the quality of the simulation $t$ :

1) Mean Absolute Error, MAE:

M A E = \frac{1}{N} \cdot \sum_{i = 1}^{N} | D o f C_{i} - \bar{D o f C_{i}} |,

where $N$ – the number of test cases, $D o f C_{i}$ – The reference value of risk collision rating for the $i$ th test case, $\bar{D o f C_{i}}$ – The value of risk collision rating for the i-th test case calculated using the logical-linguistic model.

2) Root Mean Square Error, RMSE, calculated using the formula:

R M S E = \sqrt{\frac{1}{N} \cdot \sum_{i = 1}^{N} {(D o f C_{i} - \bar{D o f C_{i}})}^{2}} .

3) Symmetric Mean Absolute Percentage Error, SMAPE, calculated using the formula [11]:

S M A P E = \frac{\sum_{i = 1}^{N} (| D o f C_{i} - \bar{D o f C_{i}} |)}{\sum_{i = 1}^{N} (D o f C_{i} + \bar{D o f C_{i}})} .

Using several test cases we will show the efficacy of the logical-linguistic model to determine the risk collision rating of ships in a heavy traffic zone.

Consider the first test situation. Assume that the speed of the OV is 15 knots and the course is 330°. According to the radar we identified that the course of TV as 330°, the bearing to the target is equal to 330° and speed of TV is 18 knots. Thus, the relative velocity is equal to 1,2. This situation is not considered dangerous because the TV moved before the OV on the same course as the TV and the TV speed is greater than OV speed, so with time the TV will be move farther and farther away from the OV. Therefore, the OV need to keep moving according to the planned course. Entering information about the location of vessels into the realized logical-linguistic model, we get the value of 0,179, which means a low risk collision rating.

Consider the second test situation. Assume that the speed of the OV is a little more than 4 knots and the course is 90°. On the radar the following information is identified: the speed of the TV is 15 knots, the course is 330°, the bearing to the target is equal to 90°. Thus, the relative speed of ships is 0,3. In this situation, the TV is located directly on the course of the OV and it is dangerous, because the range of divergence of the TV and OV is small. According to Rule No. 16 COLREG-72 [7] the OV must give way to the TV. Turning to the right at 30 degrees in a given situation will be considered sufficient because the OV will go by to the stern of the TV and the vessels will disperse at a safe distance. Since the speed of the OV is low, the decision-makers have sufficient time to assess the situation and make a decision to carry out the maneuver of divergence. This situation is characterized by an average risk collision rating. Putting information about the vessels location, we get a value of 0,5, which means an average risk collision rating.

Consider a third situation. The OV speed is 15 knots, its course is 270°. The following information is identified on radar: the speed of the TV is 20 knots, its course is 330° and the bearing to the target is equal to 180°. This situation is considered dangerous because the courses of the TV and the OV are intersecting. The TV is located to the left of the OV and is a dangerous target. According to Rule 17 (II) [7] the OV must immediately take action to avoid a collision. The risk of collision in this situation is high. Entering information about the location of vessels into logical-linguistic model we get a value of 0,844, which means a high risk collision rating.

Based on the results of modeling the following values on quality evaluations were received: MAE = 0,1235, RMSE = 0,1366, SMAPE = 0,3599. Such results demonstrate the efficiency of the logic-linguistic model presented here.

4. Conclusions

Thus, in this article we proposed logical-linguistic model for determining the risk collision rating of ships in a heavy traffic zone, introduced the input and output linguistic variables, formed the 22 terms of five basic term-sets and set the parameters of membership functions for each term. Using a maneuvering plane-table 400 fuzzy products rules of the logic-linguistic model were formed. Testing of the described model showed the adequacy of the proposed solutions to decision-makers recommendations on simulated vessels and concurrence of this solutions to COLREG-72 [7] recommendation. Further research will be focused to development the software and hardware implementation of the system for determining the risk collision rating of ships in a heavy traffic zone.

References

Song B. H., Lee K. H., Jeong M. A., Lee S. R. Bayesian collision risk estimation algorithm for efficient collision avoidance against multiple traffic vessels. The Korean Institute of Communications and Information Sciences, Vol. 36, Issue 3, 2011, p. 248-253.

Search CrossRef
Bobyr M. V., Titov V. S., Nasser A. A. Automation of the cutting-speed control process based on soft fuzzy logic computing. Journal of Machinery Manufacture and Reliability, Vol. 44, Issue 7, 2015, p. 633-641.

Search CrossRef
Chernova I. V., Sumin S. A., Bobyr M. V., Seregin S. P. Forecasting and diagnosing cardiovascular disease based on inverse fuzzy models. Biomedical Engineering, Vol. 49, Issue 5, 2016, p. 263-267.

Search CrossRef
Luneva E. E., Banokin P. I., Yefremov A. A. Evaluation of social network user sentiments based on fuzzy sets. IOP Conference Series: Materials Science and Engineering, 21st International Conference for Students and Young Scientists, 2015, p. 012054.

Search CrossRef
Antipin A. F. Improving response time of real time control systems based on multidimensional interval-logical controllers. Automation and Remote Control, Vol. 76, Issue 3, 2015, p. 480-486.

Search CrossRef
Chernyi S., Zhilenkov A. Modeling of complex structures for the ship’s power complex using XILINX system. Transport and Telecommunication, Vol. 16, Issue 1, 2015, p. 73-82.

Search CrossRef
Dolotov N. A., Palamarchuk N. A. International Regulations for Preventing Collisions at Sea (Mezhdunarodnye Pravila Preduprezhdeniy Stolknoveniy Sudov v More, 1972 Goda), Glavnoe Upravlenie Navigatsii i Okeanografii MO SSSR, Moscow, 1982, p. 87.

Search CrossRef
Yaskevich A. P., Zurabov Yu. G. Commentaries to International Rules of Preventing Collision at Sea (COLREGS) (Kommentarii k MPPSS-72). Reference Book, Transport Publications, Moscow, 1990, p. 479.

Search CrossRef
Yefremov A. A. New operations on fuzzy numbers and intervals. Proceedings of 2014 International Conference on Mechanical Engineering, Automation and Control Systems, 2014, p. 6986900.

Search CrossRef
Nyrkov A. P., Chernyi S. G., Zhilenkov A. A., Sokolov S. S. The use of fuzzy neural structures to increase the reliability of drilling platforms. Intelligent Manufacturing and Automation, Proceedings of the 26th International DAAAM Symposium, 2016, p. 672-677.

Search CrossRef
Antipin A. F. A computer-aided system for designing multidimensional logic controllers with variables representing a set of binary logic arguments. Automation and Remote Control, Vol. 74, Issue 9, 2013, p. 1573-1581.

Search CrossRef
Ramesh K., Kesarkar A. P., Bhate J., Venkat Ratnam M., Jayaraman A. Adaptive neuro fuzzy inference system for proﬁling of the atmosphere. Atmospheric Measurement Techniques Discussion, Vol. 7, 2014, p. 2715-2736.

Search CrossRef

About this article

Received

15 August 2016

Accepted

17 August 2016

Published

07 October 2016

SUBJECTS

Mathematical models in engineering

Keywords

ship collision avoidance

heavy traffic zone

linguistic variable

bearing

operator ship

target ship

fuzzy set

fuzzy production rule

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.