Oscillations of a rigid block on supported base

1. Introduction

The dynamic of solid body on a vibrating base was first considered in [1]. The author drew attention to the fact that the elongated tall free-standing structures, such as columns and water-pressure tanks, sometimes much better to suffer an earthquake, then more stable by sight constructions. This phenomenon is due to the fact that such constructions may oscillate alternately resting on one of the support ribs. Dedicated to this task a lot of publications, as in [2] found a large number of combination resonances and modes of chaotic oscillations. Considered similar tasks, taking into account slippage between the body and the support surface, the base of the elastic and the separation from the base [3-6]. Most of the results obtained by direct numerical integration. Management issues fluctuations considered in [7], there are built boundary of stability of the body in the plane of the frequency – amplitude excitations with zero initial conditions.

2. Formulation of the problem

Consider the motion of a solid parallelepiped on a horizontal supporting plane. Assume that the slippage between the plane and the parallelepiped is absent, i.e. lower base can either be fully supported on a plane, or deviate from it at an angle $\alpha$ (Fig. 1). We confine the box movements in the plane of the figure and assume that the plane of support oscillates horizontally.

Fig. 1The design scheme

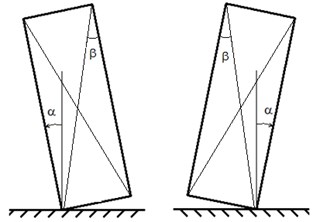
As the shock model we use Newton’s hypothesis that the relation ${\dot{\alpha }}_{+}=-R{\dot{\alpha }}_{-}$, where ${\dot{\alpha }}_{\pm }=\dot{\alpha }(t_0\pm 0)$, $t_0$ – the time at which there is shock ($\alpha \left(t_0\right)=0$), $R$ – the coefficient of restitution.

Using the theorem on change of angular momentum of the body relative to the reference ribs we get:

where $J$ – moment of inertia with respect to each of the parallelepiped supported ribs, $m$ – its mass, $d$ – half of the diagonall, $\beta$ – the angle between the vertical rib and diagonal, $g$ – acceleration of gravity, $F$ and ${\theta }_0$ – acceleration amplitude and frequency of vibrations of the plane, respectively, $r=1-R$, $\delta \left(\alpha \right)-$ normalized unit delta function, the dot denotes differentiation with respect to time.

We introduce the dimensionless time $\tau =t/{\omega }_0$, where ${\omega }_0=\sqrt{mgd\mathrm{c}\mathrm{o}\mathrm{s}\beta /J}$ and we obtain the equation of oscillations in the dimensionless form:

Where $f=F/g$, $\mu =\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(\alpha \right)$, $c=\mathrm{t}\mathrm{g}\beta$, $\theta ={\theta }_0/{\omega }_0$.

If the box height is substantially greater than the width ($c\ll 1$), the appropriate assumption of the smallness of the angle $\alpha$. If $\alpha \ll 1$ then Eq. (1) has the form:

It introduced the small parameter $\epsilon$, i.e. the amplitude of the excitation and the power dissipation is assumed to be asymptotically small that allows you to apply effective methods of nonlinear mechanics [8, 9].

At $\epsilon =0$ Eq. (2) describes the oscillations on the fixed plane of the parallelepiped. When the initial conditions $\alpha \left(0\right)=A$, $\dot{\alpha }\left(0\right)=0$ solution has the form $\alpha \left(\tau \right)=c-(c-A)ch\tau$, which is valid on a quarter of the oscillation period. From the condition $\alpha \left(\pi /\left(2\omega \right)\right)=0$ we obtain the dependence of the oscillation amplitude $A$ of the frequency $\omega$:

and a decision at one period has the form:

3. Solution

We write the solution of Eq. (2) on the one period in the form of vibrations:

here introduced the notation $B\left(\psi \right)=\psi -\left(1-\mu \right)\frac{\pi }{2}$.

New variables $A=A\left(\tau \right)$ and $\psi =\psi \left(\tau \right)$ are functions of time, and $\omega =\omega \left(A\right)$ – corresponding to Eq. (3) dependence on the amplitude of the oscillation frequency at a stationary reference plane. When $\psi =\omega \tau$ Eq. (4) corresponds to the solution of the unperturbed Eq. (2).

In the new variables the equation of oscillations of a parallelepiped have the form:

In Eq. (5) is necessary to substitute dependence:

We introduce a small frequency different $\epsilon \lambda =n\theta -m\omega$, where $n$, $m$ – mutually prime integers. Main resonance corresponds to the values $n=\mathrm{}m=\mathrm{}$1. In accordance with this assumption put $\psi =\frac{n}{m}\theta \tau -\phi$, $\dot{\psi }=\frac{n}{m}\theta -\dot{\phi }$, and we obtain the following system of equations for the slow variables $A$ and $\phi$:

Since both $A$ and $\phi$ – slow function of time, replace the Eq. (6) the time-averaged equations. In this problem the averaged equations are quite simple form for the principal resonance and combinative resonances $n=1$, $m=\mathrm{}$1, 3, 5,.... For these resonances averaged Eq. (6) up to terms of the first order have the form:

These equations allow us to find the dependence $A\left(\tau \right)$ for free oscillations of the box on a fixed plane ($f=0$) taking into account the dissipation of the impact on Newton’s model:

where $A_0=A\left(0\right)$. The second Eq. (7) in this case has the form $\dot{\psi }=\omega$, where the function can be found from Eq. (2).

Considering the forced oscillation, we confine ourselves to the steady-state oscillations (stationary mode), putting in Eq. (7) $\dot{A}=0$, $\dot{\phi }=0$. These equations together with Eq. (2) relate the amplitude and phase of oscillation $A$, $\phi$, the frequency of free oscillations $\omega$ and low frequency differens $\lambda$. The frequency of the excitation and the frequency of free oscillations associated dependency $\epsilon \lambda =n\theta -m\omega$, that allows you to build a dependence of the oscillation amplitude of the excitation frequency.

To investigate the stability of the solutions we linearize the system of Eq. (7) in the vicinity of the steady state. For asymptotic stability of stationary regimes is necessary and sufficient that the eigenvalues of the right side of the equations have negative real parts. These conditions can be obtained in an explicit form, but are not mentioned here because of their bulkiness.

4. The discussion of the results

On Fig. 2 shows the dependence $A\left(\theta \right)$ for the parameters $c=\mathrm{}$0,1; $r=\mathrm{}$0,1 and two amplitude of the base motion $f=\mathrm{}$0,01; 0,02 (curves 2 and 3 respectively). Curve 1 indicates the amplitude of the frequency of free oscillations Eq. (2). This curve fitting solutions corresponding to the main resonance. Curve 2 is built to the amplitude of the base motion $f=\mathrm{}$0,01, curve 3 – for $f=\mathrm{}$0,02. The thick lines represent stable solutions. For small excitation amplitude $f=$ 0,01 the effect of the assumed value of the parameter dissipation$\mathrm{}r=\mathrm{}$0,1 significantly, and the two solutions form a loop, the upper part of which corresponds to the stable solution.

As follows from Eq. (7), frequency deferens increases with excitation frequency, so in Fig. 2 shows the results only in low frequencies. For $f=\mathrm{}$0,02 (curve 3), even in this setting the frequency deferens $\lambda$ is not small, so the results should be regarded as qualitative. Fig. 3 shows the dependence $A\left(\theta \right)$ for parameters $c=\mathrm{}$0,1; $r=$0,02; $f=\mathrm{}$0,02. Curve 1 is the dependence $A\left(\omega \right)$. Curve 2 corresponds to the fundamental resonance, curves 3 and 4 – sub-harmonic resonance $n=\mathrm{}$1, $m=\mathrm{}$3 and $n=\mathrm{}$1, $m=\mathrm{}$5 respectively. For this family of solutions increases the frequency differences is unlimited, not only at high frequencies, but also the approach of the oscillation amplitude to the limit $A=c$.

Fig. 2The dependence of the oscillation amplitude from the excitation frequency. The main resonance

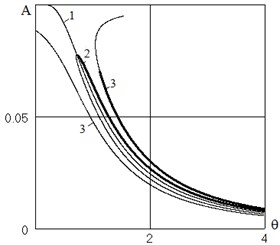
Fig. 3The dependence of the oscillation amplitudes from the excitation frequency. Combination resonances

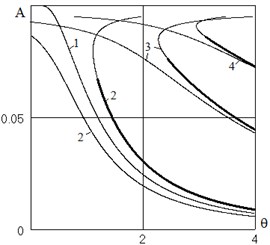
In all these cases, the amplitude of excitation is small ($f<c$), so that with zero initial conditions the body is at rest relative to the plane, and there is another stable solution $A\equiv 0$. For small oscillations of the excitation frequency for arbitrary initial conditions of a box may returns to its rest position relative to the base or overturns. With increasing excitation frequency there is one more solution – stationary oscillations in the neighborhood of the equilibrium position, the output of the main resonance. With further increase of the frequency it is possible to access to the combination resonances.

These results coincide with the exact solution [10]. The use of this paper, the averaging method has allowed not only to get the decision, but also to study their stability, which is especially important for the practical application of the results.