The polynomial dimensional decomposition method in a class of dynamical system with uncertainty

Lu, Kuan; Hou, Lei; Chen, Yushu

Vibroengineering Procedia

Browse Procedia

Published: 08 December 2016

Check for updates

The polynomial dimensional decomposition method in a class of dynamical system with uncertainty

Kuan Lu¹

Lei Hou²

Yushu Chen³

¹College of Engineering, The University of Iowa, Iowa City, IA 52242, USA

^{1, 2, 3}School of Astronautics, Harbin Institute of Technology, Harbin 150001, P. R. China

²School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, P. R. China

Corresponding Author:

Kuan Lu

Cite the article Download PDF

Downloads 1435

Abstract

In this paper, polynomial dimensional decomposition (PDD) method is applied to study the dynamical model for the first time. PDD method can reserve the amplitude-frequency characteristics of the exact solution which is obtained by the Monte Carlo simulation (MCS) method except the frequency close to the resonance, the perturbations appear around the resonance frequency. All these results are shown on the two degrees of freedom (DOF) spring system with uncertainties; the dynamical characteristics of stiffness and hybrid uncertainty uncertainty are studied in seven cases respectively. The higher PDD order approximates better to the MCS results.

1. Introduction

The dynamical analysis of multiple degree of freedom (DOF) linear system has received significant attention over the past decade. The calculating quantity of the multiple DOF (MDOF) system is very expensive and the qualitative analysis is so difficult that the MDOF system should be reduced to lower DOF one. There are a variety of efficient order reduction methods can be applied in MDOF system: center manifold method [1], inertial manifold method [2], POD method [3-5], Galerkin method [6], Lyapunov-Schmidt method [7], and other order reduction methods [8]. Rega [9] also reviewed the common order reduction methods in applied nonlinear dynamics. These methods can usually be applied in the deterministic systems and will be out of action in the stochastic systems.

On the basis of the design uncertainty, some physical parameters may vary in an uncertain way, so the response may change also in one uncertain way. The goal is to allow an estimate of the dynamic responses generated by these considerations on the actual physical parameters. Considering this, there are many different methods to take account of uncertainties in this kind of problem such as the Monte Carlo simulation (MCS) [10], polynomial chaos expansion [11], or polynomial dimensional decomposition [12]. MCS is an efficient method and well adapted to include uncertainties in a deterministic model by generating samples of the random parameters. But the computational cost of MCS is very expensive due to the reason that a large number of samples should have convergence of this method [13]. Both the PCE and PDD are the methods based on the representation of the stochastic processes and variables in a set of orthogonal bases of random variables, they are widely applied in the uncertain quantification of high-dimensional complex systems [14].

The PDD approximation commits a smaller error than does the PCE approximation for identical expansion orders when the cooperative efforts of input variables on an eigenvalue attenuate rapidly or vanish altogether [15]. Some numerical results also verify that the PDD is more efficient and the calculating time is less expensive than the PCE method [16]. The PDD method has shown to be an accurate and efficient way to solve the problems with uncertainties, so the PDD method is used in this paper.

The objective of this paper is to apply the PDD method to uncertain dynamical system in an accurate and computational-efficient manner. The amplitude-frequency characteristics of two DOF spring system with mass, stiffness, damping and hybrid case uncertainties are discuss respectively. The PDD method is compared with the MCS method to show the accuracy and efficiency of the PDD method. The influence of the PDD order is also highlighted.

2. Response of random dynamical system with harmonic excitation

In this section, uncertainties in the dynamical system are introduced first, and then we apply the PDD method to the dynamical equation.

2.1. Design uncertainties in a dynamical system

The dynamical system can be described by the $n \times n$ mass, damping, and stiffness matrices, $M$ , $C$ and $K$ , where $n$ is the DOF number. The external excitation force acting on this system can be described by $F (t)$ , and $y (t)$ is the vector of DOF.

The mass, damping and stiffness matrices are assumed to be uncertain and can be provided by:

1

M = \underline{M} (1 + c o v_{M} δ_{M}),

the stiffness, damping and mass are all assumed to be uncertain in this study. The parameters in Eqs. (1) is shown as follows, the representations of the damping and stiffness are similar as the mass: $δ_{M}$ : standard normal deviate of mass, $c o v_{M}$ : $c o v$ of mass.

The system is deterministic when the coefficient of variance ( $c o v$ ) is 0. The simple uncertainty is chosen to show the aim of this paper. We want to explain and highlight the special dynamical behaviors around the deterministic resonance frequency based on the PDD method. So this class of uncertainty will make the system clearer and more convenient to explain. It must be specified that it is the first time to apply the PDD method to solve the dynamical problems. On the basis of actually physical significance, standard normal distribution will lead to negative values of the design parameters, so we consider the control parameters are very small, the corresponding design parameters will be positive. The PDD method can not only be applied in the normal distribution but also in other distributions, such as the uniform distribution, beta distribution and so on.

The general dynamical equation can be written as:

2

M \ddot{y} (t) + C \dot{y} (t) + K y (t) = F (t) .

The external excitation is assumed to be harmonic $F (t) = F_{0} e^{i ω t}$ , and the steady state response of the system is considered as $y (t) = Y e^{i ω t}$ , where $i = \sqrt{- 1}$ , and $Y$ is the solution of the following equation:

3

(- ω^{2} M + i ω C + K) Y = F_{0},

where $M$ , $C$ , $K$ and $Y$ are the random mass, damping, stiffness and vector, which can be described by its moments. The first two moments (mean and standard deviation (SD)) are calculated. The calculating formulas of mean and SD are provided in [17]. The amplitude of the Eq. (3) is $|Y_{1} + i Y_{2}|$ , $Y_{1}$ and $Y_{2}$ are the real and complex part of $Y$ .

Actually, several methods can be used to derive these moments, such as the MCS, PCE and PDD method. In this paper, the results of MCS method will be the reference solutions and the PDD method will be compared with the MCS method.

The PDD method is an order reduction method widely applied in the stochastic systems [12], an $S$ -variate approximation PD of the response $y (x)$ , described by [18]:

4

{\tilde{y}}_{S} (x) = y_{0} + \sum_{i = 1}^{N} y_{i} (x_{i}) + \sum_{i_{1}, i_{2} = 1; i_{1} < i_{2}}^{N} y_{i_{1} i_{2}} (x_{i_{1}}, x_{i_{2}})

+ \sum_{i_{1}, i_{2}, i_{3} = 1; i_{1} < i_{2} < i_{3}}^{N} y_{i_{1} i_{2} i_{3}} (x_{i_{1}}, x_{i_{2}}, x_{i_{3}}) + \dots + \sum_{i_{1}, \dots, i_{S} = 1; i_{1} < \dots i_{S}}^{N} y_{i_{1} \dots i_{S}} (x_{i_{1}}, \dots, x_{i_{S}}),

can be viewed as a finite hierarchical expansion of an output function in terms of the input variables with the increasing dimensions, and $y_{0}$ is a constant, $y_{i} (x_{i})$ is a univariate component function that represents individual contribution to $y (x)$ by input variable $x_{i}$ acting alone. In a similar way, $y_{i_{1} i_{2}} (x_{i_{1}}, x_{i_{2}})$ is a bivariate component function, $y_{i_{1} i_{2} i_{3}} (x_{i_{1}}, x_{i_{2}}, x_{i_{3}})$ is trivariate and $y_{i_{1} \dots i_{S}} (x_{i_{1}}, \dots, x_{i_{S}})$ is a an $S$ -variate component function. When $S \to N$ , the response converges to the exact function $y (x)$ .

Here, we give the approximate expressions of the first variate component functions, described by:

5

y_{i} (x_{i}) ≅ \sum_{j = 1}^{m} α_{i j} ψ_{i j} (x_{i}),

where $α_{i j}$ is the corresponding coefficients, see details in [12].

2.2. Dynamical equation based on PDD

As is mentioned above, the DOF vector $y (t)$ is random, and $y (t)$ is a solution to the dynamical Eq. (2), where $M$ is defined by Eq. (1), the damping and stiffness terms are similar. An $S$ -variate approximation of the PDD of response $y (t)$ can be express as:

6

{\tilde{y}}_{S} (X) ≅ y_{0} + \sum_{i = 1}^{N} \sum_{j = 1}^{m} α_{i j} ψ_{i j} (X_{i}) + \sum_{i_{1}, i_{2} = 1; i_{1} < i_{2}}^{N} \sum_{j_{2} = 1}^{m} \sum_{j_{1} = 1}^{m} β_{i_{1} i_{2} j_{1} j_{2}} ψ_{i_{1} j_{1}} (X_{i_{1}}) ψ_{i_{2} j_{2}} (X_{i_{2}})

+ \sum_{i_{1}, i_{2}, i_{3} = 1; i_{1} < i_{2} < i_{3}}^{N} \sum_{j_{3} = 1}^{m} \sum_{j_{2} = 1}^{m} \sum_{j_{1} = 1}^{m} γ_{i_{1} i_{2} i_{3} j_{1} j_{2} j_{3}} ψ_{i_{1} j_{1}} (X_{i_{1}}) ψ_{i_{2} j_{2}} (X_{i_{2}}) ψ_{i_{3} j_{3}} (X_{i_{3}})

+ \dots + \sum_{i_{1}, \dots, i_{S} = 1; i_{1} < \dots < i_{S}}^{N} \sum_{j_{S} = 1}^{m} \dots \sum_{j_{1} = 1}^{m} C_{i_{1}, \dots, i_{S} j_{1}, \dots, j_{S}} \prod_{k = 1}^{S} ψ_{i_{k} j_{k}} (X_{i_{k}}),

as $m \to \infty$ , Eq. (6) converges to $y (t)$ in the mean square sense for $S = N$ . Then the dimension reduction method [12] is applied to calculate the coefficients $y_{0}$ and $C_{i_{1}, \dots, i_{S} j_{1}, \dots, j_{S}}$ . In this paper, we only use the univariate method to study the simple model. There is no need to use the bivariate or trivariate method, for the system is linear and there are at most 3 variables. The univariate results can approximate to the MCS results.

The formulas of the PDD method to calculate the response moments of a stochastic system are shown in ref. [17], on the basis of the discussions above, the components of the PDD can satisfy the following equation:

7

\bar{M} \ddot{\bar{x}} (t) + \bar{C} \dot{x} (t) + \bar{K} x (t) = \bar{F} (t),

so the dynamical system with uncertainty can be regarded as the deterministic one. Then we can apply PDD method to study the stochastic moments of the amplitude of the dynamical system.

3. Two-DOF spring model

The two-DOF spring model will be established by the Newton’s second law, the PDD and MCS methods will be used to calculate the mean and SD of the response for the model shown in Fig. 1.

The dynamical equation of the spring model is similar as Eq. (2), and the corresponding parameters are shown in Eq (8):

8

M = (\begin{array}{l} m_{1} \\ m_{2} \end{array}), C = (\begin{array}{l} c_{1} + c_{2} & - c_{2} \\ - c_{2} & c_{2} + c_{3} \end{array}), K = (\begin{array}{l} k_{1} + k_{2} & - k_{2} \\ - k_{2} & k_{2} + k_{3} \end{array}), F (t) = (\begin{array}{l} F_{1} \\ F_{2} \end{array}) .

The stiffness, damping and mass are assumed to be uncertain: we assume that the damping is equal to each other, so as the stiffness and mass; we sign the stiffness, damping and the mass as $k$ , $c$ and $m$ respectively. The corresponding values are shown in Table 1.

The mass, damping and the stiffness are assumed to be uncertain, the formulas are shown in Eq. (9):

9

m = \bar{m} (1 + c o v_{m} δ_{m}),

where $c o v_{m}$ , $c o v_{c}$ , $c o v_{k}$ are the $c o v$ parameters and $\bar{m}$ , $\bar{c}$ , $\bar{k}$ are the mean values.

Fig. 12-DOF spring model

Table 1Corresponding values

$m$ (kg)	$c$ (Nm^-1 s^-1)	$k$ (Nm^-1)	$c o v_{m}$	$c o v_{c}$	$c o v_{k}$	$F_{1}$ (N)	$F_{2}$ (N)
1	1	15000	3 %	4 %	5 %	1	0

4. Dynamical characteristics of the spring system

In this section, the sole design uncertainty is discussed first, for example, the stiffness, damping and stiffness uncertainties. Later, the amplitude-frequency characteristics of the hybrid uncertainty are studied. The DOF vector was calculated for 1001values of $ω / (2 π)$ in the range of 15-40 Hz, the step is length is 0.025 Hz.

The MCS results were obtained with 10000 samples of the random variables $δ_{m}$ , $δ_{c}$ , $δ_{k}$ . The first two moments (mean and SD) are plotted in Fig. 2-Fig. 3. The PDD order is calculated for both 2 and 9 to verify the influence of high order PDD.

4.1. Stiffness uncertainty

The mean and SD of PDD order 2 is plotted in Fig. 2(a) and (b), the mean preserves the amplitude-frequency trend of the MCS result, the SD is in perfect agreement with the MCS result. Both mean and SD calculated by PDD have oscillations around the resonance. The curves oscillate more and the vibration amplitude decreases as the PDD order increases, which are shown in Fig. 2(c) and (d). The higher PDD order can approximate to MCS better.

Fig. 2Amplitude frequency curves of PDD (black line) and MCS (blue line)

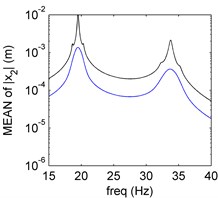
a) Mean of PDD order 2

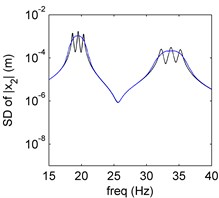
b) SD of PDD order 2

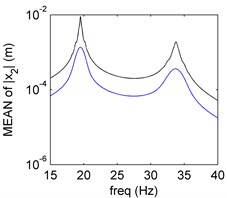
c) Mean of PDD order 9

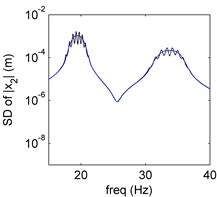
d) SD of PDD order 9

Fig. 3Amplitude frequency curves of PDD (black line) and MCS (blue line)

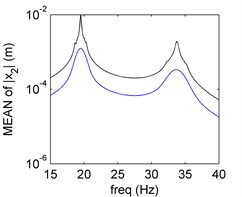
a) Mean of PDD order 2

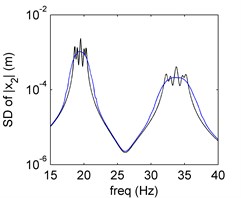
b) SD of PDD order 2

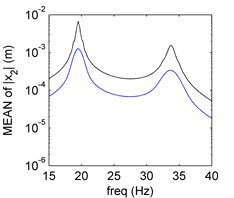
c) Mean of PDD order 9

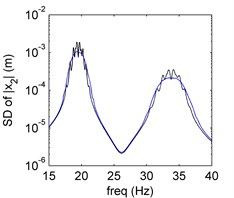
d) SD of PDD order 9

4.2. Hybrid uncertainty

We will study the hybrid uncertainty of the 2-DOF spring system in this section. The corresponding uncertain parameters and the order are listed in Table 2, one case is provided and the other cases will be discussed later.

In Fig. 3, it is clear that the PDD results agree well with the exact solutions obtained by the MCS results. The frequency-amplitude characteristic of the second moment is more complex than the single uncertainty.

Table 2Corresponding uncertain parameters

Case	$δ_{k}$	$δ_{c}$	$δ_{m}$	Order	Order
1	0.05	0.04	0.03	2	9

5. Conclusions

The PDD method is applied to study the dynamical characteristics of the random dynamical system for the first time. A two DOF spring system is established, the amplitude-frequency characteristics of mass and the hybrid uncertainties are discussed based on the design uncertainties respectively. The accuracy and efficiency of the PDD method is verified via comparing with the MCS method. Meanwhile, the higher order PDD is also studied and the results can approximate to the exact solutions obtained by the MCS method better.

References

Alho A., Uggla C. Global dynamics and inflationary center manifold and slow-roll approximants. Journal of Mathematical Physics, Vol. 56, 2015, p. 012502.

Search CrossRef
Chung Y. M., Steyer A., et al. Global error analysis and inertial manifold reduction. Journal of Computational and Applied Mathematics, Vol. 307, Issue 1, 2016, p. 204-215.

Search CrossRef
Lu K., Yu H., Chen Y. S., Cao Q. J., Hou L. A modified nonlinear POD method for order reduction based on transient time series. Nonlinear Dynamics, Vol. 79, Issue 2, 2015, p. 1195-1206.

Search CrossRef
Lu K., Jin Y. L., Chen Y. S., Cao Q. J., Zhang Z. Y. Stability analysis of reduced rotor pedestal looseness fault model. Nonlinear Dynamics, Vol. 82, Issue 4, 2015, p. 1611-1622.

Search CrossRef
Lu K., Chen Y. S., Jin Y. L., Hou L. Application of the transient proper orthogonal decomposition method for order reduction of rotor systems with faults. Nonlinear Dynamics, Vol. 86, Issue 3, 2016, p. 1913-1926.

Search CrossRef
Zhu J., Zhong X. H., et al. Runge-Kutta discontinuous Galerkin method with a simple and compact hermite WENO limiter. Communications in Computational Physics, Vol. 19, Issue 4, 2016, p. 944-969.

Search CrossRef
Li C. P., Ma L. Lyapunov-Schmidt reduction for fractional differential systems. Journal of Computational and Nonlinear Dynamics, Vol. 11, Issue 5, 2016, p. 051022.

Search CrossRef
Hamilton N., Tutkun M., Cal R. B. Low-order representations of the canonical wind turbine array boundary layer via double proper orthogonal decomposition. Physics of Fluids, Vol. 28, 2016, p. 025103.

Search CrossRef
Rega G., Troger H. Dimension reduction of dynamical systems: methods, models, applications. Nonlinear Dynamics, Vol. 41, 2005, p. 1-15.

Search CrossRef
Li M. Q., Yang F. A metamodel-based Monte Carlo simulation approach for responsive production planning of manufacturing systems. Journal of Manufacturing Systems, Vol. 38, 2016, p. 114-133.

Search CrossRef
Jacquelin E., Friswell M. I., et al. Polynomial chaos expansion with random and fuzzy variables. Mechanical Systems and Signal Processing, Vol. 75, 2016, p. 41-56.

Search CrossRef
Rahman S. A polynomial dimensional decomposition for stochastic computing. International Journal for Numerical Methods in Engineering, Vol. 76, 2008, p. 2091-2116.

Search CrossRef
Didier J., Sinou J. J., Faverjon B. Study of the non-linear dynamic response of a rotor system with faults and uncertainties. Journal of Sound and Vibration, Vol. 31, 2012, p. 671-703.

Search CrossRef
Rahman S. The f-sensitivity index. SIAM/ASA Journal of Uncertainty Quantification, Vol. 4, Issue 1, 2016, p. 130-162.

Search CrossRef
Rahman S., Yadav V. Orthogonal polynomial expansions for solving random eigenvalue problems. Internation Journal of Uncertainty Quantification, Vol. 1, Issue 2, 2011, p. 163-187.

Search CrossRef
Yadav V. Novel Computational Methods for Solving High-Dimensional Random Eigenvalue Problems. Ph.D. Thesis, University of Iowa, 2013.

Search CrossRef
Rahman S. Statistical moments of polynomial dimensional decomposition. Journal of Engineering Mechanics (ASCE), Vol. 136, Issue 7, 2010, p. 923-927.

Search CrossRef
Xu H. Q., Rahman S. Decomposition methods for structural reliability analysis. Probabilistic Engineering Mechanics, Vol. 20, 2005, p. 239-250.

Search CrossRef
Xu H. Q., Rahman S. A generalized dimension-reduction method for multi-dimensional integration in stochastic mechanics. International Journal for Numerical Methods in Engineering, Vol. 61, 2004, p. 1992-2019.

Search CrossRef

About this article

Received

02 November 2016

Accepted

03 November 2016

Published

08 December 2016

SUBJECTS

Mechanical vibrations and applications

Keywords

polynomial dimensional decomposition

Monte Carlo simulation

order reduction

dynamical characteristic

uncertainty

Acknowledgements

We appreciate for the financial supports from the National Basic Research Program (973 Program) of China (Grant No. 2015CB057405).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.