Reliability of chatter stability in CNC turning process by Monte Carlo simulation method

1. Introduction

In numerical control turning operations, cutting vibration seriously contributes in affecting the workpiece machineability, and hence, lowers the finished part quality. Previous research demonstrated that the cutting vibration is often caused by regenerative feedback inside the system which is termed as self-excited vibration or cutting chatter [1]. In general, chatter in machining process can be categorized as regenerative cutting chatter, vibration mode coupled cutting chatter and negative friction cutting chatter. It is well known that regenerative chatter is the most important form of vibration which deleteriously affecting the machining process [2, 3]. Usually for solving the machining chatter instability issue, dynamic model analysis of the system, which includes the influence of axial cutting force and gyroscopic effect on chatter stability, must be introduced. Then dynamic cutting experiments should be performed in order to verify the correctness of the theoretical model [4-6]. Similar procedure was employed in the chatter prediction of milling operation using continuous wavelet features and multi class ball support vector machines (SVM) where stiffness and damping were optimized [7]. In other research works Y. Altintas et al. [8] investigated the influence of the vibration coupling on the machining stability of CNC machine tool subsystem. P. Albertelli et al. [9] established chatter stability analysis model for heavy duty milling machine to optimize the process planning and tool selection process. However, the stability analysis model of traditional cutting chatter ignores the influence of uncertain factors, which will inevitably lead to certain analysis errors. In machining practice, usually there are few deterministic factors, most of which are stochastic factors inherent in the process of metal cutting and cannot be ignored. Accordingly, the practical machining process is very likely to have performance deviation, and it is often difficult to achieve the exact desired effect. In this study, we intended to take into consideration the effect of random factors in the stability of the CNC turning operation. Therefore, a generalized method for predicting the reliability of chatter stability for this process is intended to be achieved by using Monte Carlo numerical simulation.

2. Analysis of the regenerative chatter

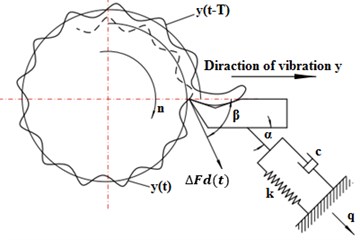
The regenerative chatter analysis of the turning process in question is based on the difference between cutting thickness caused by the phase difference and the vibration displacement [10]. Fig. 1 represents the dynamic model of regenerative chatter system for this process. Accordingly, the differential equation of vibration [1, 3] is given as follows:

where $m$ is the equivalent mass of lathe tool system, $c$ is the equivalent resistance, $k$ is the equivalent stiffness, $\beta$ is the angle between the dynamic cutting force, $\mathrm{\Delta }{F}_d\left(t\right)$ is the tool vibration direction, $\alpha$ is the angle between the main vibration direction and $q\left(t\right)$ is the direction of tool vibration.

Fig. 1Dynamic and inertia model of the vibrated system

The dynamic cutting force $\mathrm{\Delta }{F}_d\left(t\right)$ is generally caused by the variation in the cutting thickness, and can be expressed by the follows relationship:

where $b$ is the cutting width, $kc$ is the stiffness coefficient per unit width of cut, $y\left(t\right)=q\left(t\right)\mathrm{c}\mathrm{o}\mathrm{s}\alpha$ is the cutter vibration displacement, $0<\mu <1$ is the overlap coefficient of twice cutting.

By substituting Eq. (2) into Eq. (1) the differential equation of regenerative chatter can be rearranged as follows:

where ${\omega }_n$ is the natural angular frequency of the vibrated system, ${\omega }_n^2=k/m$, $\zeta$ is the damping ratio, $\zeta =c/\left(2m{\omega }_n\right)$ and $u=\mathrm{c}\mathrm{o}\mathrm{s}(\beta –\alpha )\mathrm{c}\mathrm{o}\mathrm{s}\alpha$ is the directional coefficient.

The dynamic response of turning vibration is given by the following expression:

Substitution Eq. (4) into Eq. (3), we can obtain expression for Eq. (5) as follows:

By employing Laplace transformation to Eq. (5), we can obtain the characteristic equation of the chatter system as follows:

Hence, the stability state of the vibrated system can be judged by the root of Eq. (6) where $s=\sigma +i\omega$. Then if the real part of $s$ is $\sigma >0$, the turning process system is in unstable state. However, when $\sigma <0$ the turning process is considered to be in stable state. Otherwise, the turning process system is in limiting state when $\sigma =$ 0. Therefore, in Eq. (6) the value of $s$ was replaced by $i\omega$ and the equation became as follows:

If the real parts in the left and right sides of the Eq. (7) are feasible, then should be respectively equal. Thus, the following expressions were concluded:

Assuming that that $\lambda =\omega /{\omega }_n\text{,}$ then Eq. (8) can be further converted to the following expression:

By Solving Eq. (9), the limit cutting width of machine tool is obtained:

And the corresponding spindle speed $\left(N\right)$ is given by the following relationship:

By substituting the dynamic parameters $k$, $c$, $m$, $\alpha$, $\beta$, $kc$, and $\mu$ in Eqs. (10) and (11), the limit cutting width for the stable machining $b_{lim}$ and the corresponding spindle speed $N$ at $j=$ 0, 1,…, $n$, can be obtained.

By substituting $\mu =$ 1 into Eq. (9), with a larger overlap coefficient of cutting, the chatter can be easily generated, the minimum limiting width of cut for stable machining is expressed as follows:

3. Reliability expressions for Monte Carlo simulation

In general, mechanical reliability refers to the ability of mechanical products to complete the specified function in the exact required service period, and it can be a measurable value. The two-common method for measuring the reliability are the moments method and Monte Carlo simulation. Comparing Monte Carlo simulation with moment method, the former one has the advantage of high universality and high precision [11]. However, Monte Carlo method is based on a large number of simulation and calculations, which is not suitable for predicting the reliability of complex numerical models as finite element method. As the case in this study does not involve complicated numerical model, Monte Carlo simulation is an appropriate tool to be used here, since numerical control cutting width is an explicit expression. Therefore, the chatter stability of the CNC turning operation was predicted and compared in the term of cutting width. Thus, the reliability of the turning system stability can be described as a multidimensional integral, given by:

where $x_1$, $x_2$,..., $x_n$ are random design variables ($k$, $\zeta$, ${\omega }_n$, $\mu$, $u$, $k_c$), $n$ is the number of random design variables, $fx$($x_1$, $x_2$,…, $x_n$) the joint probability density function of random design variables.

If the design variables are independent of each other, Eq. (13) can be rewritten as follows:

where $f{x}_i\left(x_i\right)(i=1,2,...,n)$is probability density function of $x_i$ of random variables.

The basic idea is that the reliability of turning chatter stability indeed can be solved by using MCS method where the $N$ groups of random samples $x_j$ ($j=$ 1, 2,…, $N$) are generated from the probability density function (PDF) $f_{xi}\left(x_i\right)$ of random variable $X_i$. The $N$ random samples are substituted into the function expression of limiting width of cut for stable machining as represented by Eq. (10). Then, it is counted for the number of sample points $Nr$ that $b_{lim}$ is greater than the actual cutting width $b$, and the reliability $Ps$ is approximately replaced by using a frequency that is corresponding to $Nr/N$ as in the following expression:

where:

Is the indicator function in the security domain $R^n$; $n$ is dimensional variable space; and $E\left(\right)$ represents of the mathematical.

4. Calculation and estimation of chatter stability

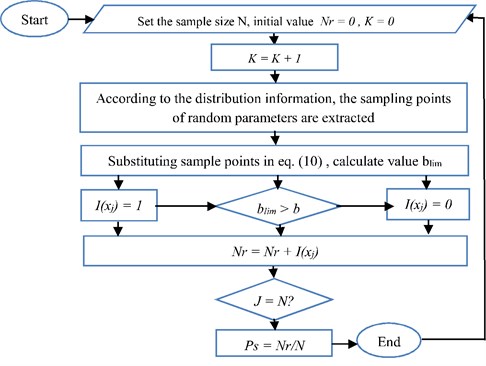
Fig. 2 reveals the followed steps to obtain the estimated numerical values for the reliability of chatter stability as function of cutting width and the machine spindle speed. In the first step, we need to determine the number of simulation $N$. Secondly the $N$ groups of samples are extracted according to the information distribution of the design parameters. Thirdly, the machining stability is changed by the sample generation analysis of the model to calculate the ultimate cutting width ($b_{lim}$). In the final step, the reliability of the machine stability is calculated. This requires taking into consideration the characteristic parameters of the CNC lathe machine during cutting process Table 1. Therefore, the characteristics parameters values of the lathe machine were substituted in Eqs. (9), (10) and (11) respectively in order to obtain the output data for cutting width with the spindle speed. After then the results were plotted in the lobe graph of the CNC lathe as shown in Fig. 3. It can be seen that the limiting cutting width is varied with the spindle speeds, and the minimum limiting cutting width ($b_{lim}$) min is equal to 0.36 mm. Then Monte Carlo simulation method was used to estimate the reliability of the process chatter stability, which is mainly based on statistical analysis of the data. Generally, the variance of random parameters can be obtained by the reliability testing or the statistical analysis of experimental data. However, in the current case there is no experimental data, and thus, the variance of the random parameters can be determined from the variation coefficient $\left(C\right)$ which is set to be equal to 0.05. In this case, the random parameters are said to obey the statistical normal distribution, if a large number of independent factors [12, 13] influence the random variables.

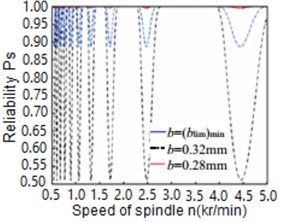
By following the steps in Fig. 2 using 105 Monte Carlo sampling simulations, the limit cutting widths and the equivalent reliability of chatter stability were estimated. Fig. 4 shows the result obtained from the simulation. It can be seen that the very good stability of the machine chatter was obtained at cutting width equal to 0.28 mm, while the poorest machine stability occurs at cutting width of ($b_{lim}$) where the equivalent reliability is only 52 % (Table 2).

Fig. 2Flowchart for calculating chatter stability reliability

5. Conclusions

Based on Monte Carlo simulation, the reliability of regenerative chatter stability was calculated. In Comparison with the traditional cutting force prediction method, Monte Carlo simulation take into consideration the influence of the random parameters such as stiffness, damping, mass and cutting stiffness coefficient on the cutting process stability. It can well predict with very close approximation to the actual situation of the process. Furthermore, different spindle speed for turning process can be predicted where good machine stability is attained. This study provided information on how to improve the machining accuracy, ensure long tool life and increasing production rate. The output of this study is expected to have practical application in manufacturing engineering.

Fig. 3Stable lobe graph of CNC turning operation

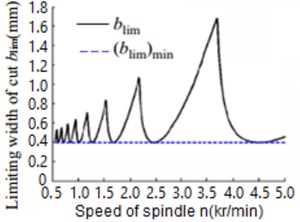
Fig. 4Reliability of chatter stability of CNC turning operation by MCS method