Damping effect on chatter stability of turning and milling processes

2.1. Model analysis of turning process

The dynamic equation of a single degree of freedom damped turning system can be described as follows:

where: $m$, $c$, $k$ are system mass, damping viscosity, and stiffness respectively, $y\left(t\right)$ is the amount of vibration in the $Y$ direction, $F_f$ is the feed force and $F_p$ is the damping force. The process damping force, $F_p$, can be expressed as a function of velocity, $v$, chip width, cutting speed, and a constant $c$ [16]. See Eq. (2):

where: $C$ is the damping coefficient. By substituting Eq. (2) into Eq. (1), the dynamic equation of the damped turning process can be obtained as follows:

Hence, the frequency response function of the system in the $Y$ direction can be written in the following way:

To describe the stability algorithm, consider a single degree of freedom turning operation with regenerative chatter [17]. Thus, the limiting stable chip width, $b_{lim}$, for regenerative chatter can be determined using the following equation:

where: $\mathrm{\Phi }\left(\omega \right)$ is the oriented frequency response function, $K_f$ is the cutting force coefficient in the feed direction, and $\mathrm{R}\mathrm{e}$ is the real part function.

The relationship between the spindle speed, $\mathrm{\Omega }$, and the valid chatter frequencies, $f_c$ (i.e., those frequencies where the real part of $\mathrm{\Phi }\left(\omega \right)$ is negative) are given by the follwing expression:

where $S=$ 0, 1, 2,… is the integer number of waves per revolution (i.e., the lobe number), and $\epsilon =2\pi -2\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{\mathrm{R}\mathrm{e}\left(\Phi \left(\omega \right)\right)}{\mathrm{I}\mathrm{m}\Phi \left(\omega \right)}$, (rad) is the phase between the current vibration and the previous pass, $\mathrm{R}\mathrm{e}\left(\mathrm{\Phi }\left(\omega \right)\right)$, $\mathrm{I}\mathrm{m}\left(\Phi \left(\omega \right)\right)$ are the real and imaginary parts of the oriented transfer function.

2.2. Model analysis of milling process

The dynamic equation of the two degrees of freedom damped milling system can be expressed as:

where $q$ is the response of the system under the action of force $F$, and $M$, $C$, $K$ is the system mass, damping viscosity, and stiffness respectively. Eq. (7) can be written in the matrix form as follows:

In addition, the frequency response function $G\left(\omega \right)$ of the system can be expressed as follows:

The harmonic response ($q$) at the critical chatter frequency (${\omega }_c$) is given as follows:

The dynamic cutting force in milling process can be expressed as follows:

where: $a_p$ is the axial cut depth, $K_t$ is the tangential force coefficient, $C_{eq}$ is the equivalent damping, $A_0$ and $B_0$ are zero order harmonics, respectively, and are related to the radial force coefficient and the friction factor respectively [10]. The milling force $F$ in an exponential form can be expressed as follows:

Thus, we can be obtained a simultaneous solution for the Eqs. (10) and (13) as follows:

where $\mathrm{\Lambda }$ is the eigen value of the characteristic solution of the dynamic milling equations at the frequency domain, and can be expressed as follows:

Take $\mathrm{\Lambda }={\mathrm{\Lambda }}_R+i{\mathrm{\Lambda }}_I$ and $e^{-{\omega }_{c}T}=\cos \left({\omega }_{c}T\right)-i\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_{c}T\right)$, and substitute these values in Eq. (15) to obtain an expression for the critical axial cutting depth ($a_p$) as follows:

Since the axial depth of cut is real, the imaginary part of Eq. (16) is equal to zero, ${\bigwedge }_I\left(1-\cos \left({\omega }_{c}T\right)\right)+{\bigwedge }_R\sin \left({\omega }_{c}T\right)=0$. Hence, the relation between the imaginary characteristic value and real characteristic value of the solution can be written as follows:

By substitution Eq. (17) into Eq. (16), the critical axial cutting depth can be expressed as follows:

The phase angle between the internal and external modulation ($\epsilon$), is given as function of the characteristic values of phase shift $\mathrm{\Psi }=\arctan \left(s\right)$ and critical limit cutting depth in the following formula:

The spindle speed is expressed as follows:

where: ${\omega }_c$ is critical chatter frequency and $S$ is an integer number of vibration waves.

3.1. Turning process

Based on the above principle, a simulation program of turning stability considering the influence of process damping is developed by Matlab, and the flow chart is shown in Fig. 2.

In order to study the influence of damping process on cutting stability, a simulation is carried out to analyze the process with/without damping. the experimental data of machining with the titanium Nitride cutting tool are given in Table 1.

According to the simulation results, the cutting stability was tested for the process with/without damping (Fig. 2). It can be noticed that the process with damping effect gains more stability at low cutting speeds than without damping. Thus, at spindle speed lower than 4000 rev/min, the process stability with damping effect is much better at larger cutting depth (Fig. 2(b)). In this case, the estimated axial cutting depth is higher compared to the that obtained for the process without damping (Fig. 2(a)). This indicates that turning process with damping effect has improved the process stability when machining at low cutting speed as well as participated in increasing the material removable rate.

Fig. 1Flow chart of stability for turning operation considering the effect of process damping

Fig. 2Effect of the process with/without damping on the chatter stability of the turning process

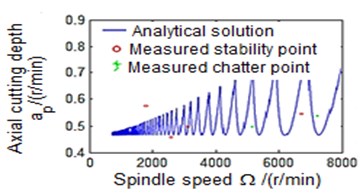
a) Process damping effects are not considered

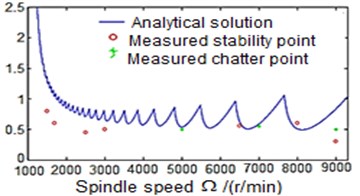
b) Consider process damping effects

3.2. Milling process

A similar procedure is used for simulating the milling process with/without damping. This is also achieved by making use of the data from actual milling test (Table 2), and the developed mathematical models in Matlab/Simulink software. Therefore, milling process with and without damping is simulated. Fig. 4 shows the simulation follow chart for the process with damping effect. In addition, the results from the simulation are verified by the actual experimental test where the frequency response function of the machine tool system is processed using the CutPro software. The spindle speed is set varied from 1000-3800 rev/min at 500 rev/min increments. The cutting starts at a minimum axial depth of 0.5 mm with 0.5 mm increments until chatter occurs. Fig. 5 shows the experimental setup of the damping milling process.

Fig. 3The setup of the damped milling process test

Fig. 4Flow chart of stability for milling process considering the effect of process damping

Fig. 5 reveals the stability levels of the milling process with/without damping. It can be noticed that the simulated process with damping shows higher machining stability at cutting depth slightly greater than 3 mm when the operating speed is below 2000 rev/min (Fig. 5(b)). This result is consistent with that obtained from experimental test where the machine stability for the above-mentioned speed occurs at cutting depth of almost 3 mm. Conversely, in the case of the undamped milling process, the machining stability is obtained when the operating speed is below 2000 rev/min at cutting depth less than 3 mm (Fig. 5(a)). Thus, the process with damping allows the removable rate to be increased, and at the same time keeps the machining process stable. This will have a good impact on the quality of the machined parts surface finish, and preserves the cutting tool life.

Fig. 5Effect of the process with/without damping on the stability of the milling process

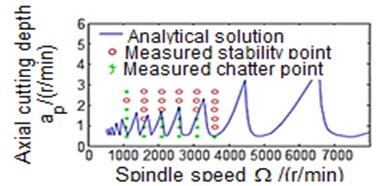
a) Process damping effects are not considered

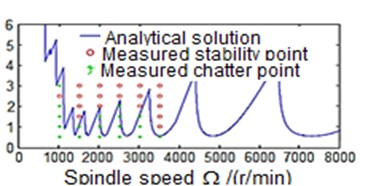
b) Consider the influence of process damping