Bending vibrations of stepped rods

1. Introduction

A rod with a mass distributed along its length is considered as a system with an infinite number of degrees of freedom. The position of the rod at any time is determined by its elastic line, which is a function of two variables: the coordinates along the length ($x$) and the time ($t$). To determine the fundamental vibrations of such systems, the ratios of the theory of bending of rods, known from the discipline Resistance of materials, are used. There are exact solutions for plain rods with various types of supports. The exact solutions are obtained using so called “fundamental beam functions”. For rods and rod systems, which elements have a variable cross-section, finding exact methods for calculating frequencies and principal modes of vibration is a very difficult problem. Therefore, it is urgent to develop and use approximate methods for solving such problems [1-10].

2. Object and subject of research

The research considers the bending vibrations of single-span stepped rods with the same and different types of supports at the ends: hinged at both ends, fixed at both ends, hinged at one end and fixed the other end. A stepped rod consists of several segments with dimensions taken in accordance with the ability to resist the stresses induced by loads (more stressed segments have a larger cross-section, less stressed ones have a smaller cross-section). A rod in bending is also called a beam. The fundamental frequency of vibration is defined considering different lengths and stiffness ratios of stepped rod segments.

3. Solution

3.1. A stepped rod fixed at both ends

A rod consisting of three segments has a span $l$. The segments at supports have length $kl$ and stiffness $EI$, the middle segment has length (1-2 $k$)$l$ and stiffness $nEI$ (see Fig. 1).

Fig. 1A stepped rod fixed at both ends

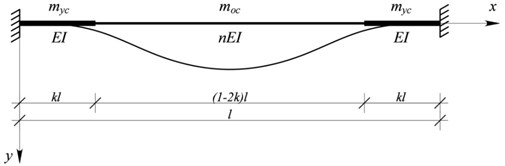
To define the fundamental vibration frequency squared for a rod, the approximate Lagrange-Ritz method [10] can be used. In accordance with the method, the $k$th vibration frequency squared can be defined by the following equation:

1

${\omega }_k^2=\underset{0}{\overset{l}{\int }}EI\left(x\right){\left[{\varphi }_1^{\text{'}\text{'}}\left(x\right)\right]}^{2}dx/\underset{0}{\overset{l}{\int }}m\left(x\right){\varphi }_1^2\left(x\right)dx,$

where ${\phi }_1\left(x\right)$ is a deflection function; $m\left(x\right)$ is the mass per unit length of a rod.

Let us take the deflection function of the rod in the given coordinate system as follows:

2

${\varphi }_1\left(x\right)=a\left(1-\mathrm{c}\mathrm{o}\mathrm{s}\frac{2\pi x}{l}\right),$

where $a$ – const.

The given function satisfies all boundary conditions. With all necessary transformations completed, taking into account the average value of mass per length unit, we obtain the following:

3

${\omega }_1^2=\frac{64EI{\pi }^4}{3l^4\overline{m}}\cdot \left[\frac{1}{2}\left(k+\frac{\mathrm{s}\mathrm{i}\mathrm{n}4\pi k}{4\pi }\right)+n\left(\frac{1}{4}-\frac{1}{2}\left(k+\frac{\mathrm{s}\mathrm{i}\mathrm{n}4\pi k}{4\pi }\right)\right)\right],$

where $\overline{m}=2\left(k\cdot m_{yc}+\mathrm{0,5}\left(1-2k\right)\cdot m_{oc}\right)$ – is the average mass per unit length.

By substituting the parameters $n=$ 1 and $k=$ 0 (or 0.5) into the Eq. (3), which corresponds to a plain rod, we obtain the following:

${\omega }_1^2=\frac{{\left(\mathrm{1,519}\pi \right)}^2}{l^2}\cdot \sqrt{\frac{EI}{\overline{m}}},$

which differs from the exact solution [1]:

${\omega }_1^{}=\frac{{\left(\mathrm{1,5}\pi \right)}^2}{l^2}\cdot \sqrt{\frac{EI}{\overline{m}}}\text{by}\text{2.64}\text{\%}\text{.}$

Thus, the solution Eq. (3) gives acceptable result.

3.2. A stepped rod with hinged ends

A rod consisting of three segments has a span $l$. The segments at supports have length $kl$ and stiffness $nEI$, the middle segment has length (1-2 $k$)$l$ and stiffness $EI$ (see Fig. 2).

Fig. 2A rod with hinged ends

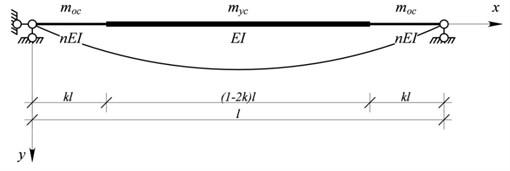
Let us use the Lagrange-Ritz method. We take a deflection function as follows:

4

${\varphi }_1\left(x\right)=\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi x}{l}.$

The given function satisfies all boundary conditions. With all necessary transformations completed, taking into account the average value of mass per length unit, we obtain the following:

5

${\omega }_1^2=\frac{4EI{\pi }^4}{l^4\overline{m}}\cdot \left[\frac{1}{2}\left(k-\frac{\mathrm{s}\mathrm{i}\mathrm{n}2\pi k}{2\pi }\right)\cdot \left(n-1\right)+\frac{1}{4}\right],$

where $\overline{m}=2\left(k\cdot m_{oc}+\mathrm{0,5}\left(1-2k\right)\cdot m_{yc}\right)$ – is the average mass per unit length.

By substituting the parameters $n=$ 1 and $k=$ 0 (or 0.5) into the Eq. (5), which corresponds to a plain rod, we obtain the exact solution [1]:

${\omega }_1^{}=\frac{{\pi }^2}{l^2}\cdot \sqrt{\frac{EI}{\overline{m}}}.$

3.3. A stepped rod fixed at one end and hinged at the other end

A rod consisting of two segments has a span $l$. The segment on the side with fixed end has length $kl$ and stiffness $EI$, the segment on the side with hinged end has length (1-$k$)$l$ and stiffness $nEI$ (see Fig. 3).

Fig. 3A stepped rod fixed at one end and hinged at the other end

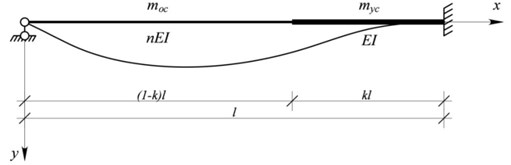
Let us use the Lagrange-Ritz method. For a deflection function we take the equation of the elastic line of a plain rod under uniformly distributed load $q$ along the entire length:

6

${\varphi }_1\left(x\right)=A\cdot \left(-l^{3}x+3l{x}^3-2x^4\right),$

where $A=q/48EI$.

The given function satisfies all boundary conditions. With all necessary transformations completed, taking into account the average value of mass per length unit, we obtain the following:

7

${\omega }_1^2=\frac{630EI}{19l^4\overline{m}}\cdot \left[\left(108{\left(1-k\right)}^3-216{\left(1-k\right)}^4+\mathrm{115,2}{\left(1-k\right)}^5\right)\cdot \left(n-1\right)+\mathrm{7,2}\right],$

where $\overline{m}=\left(1-k\right)\cdot m_{oc}+k\cdot m_{yc}$ is the average mass per unit length.

By substituting the parameters $n=$ 1 and $k=$ 0 (or 1) into the Eq. (7), which corresponds to a plain rod, with number $\pi$ intentionally introduced, we obtain the following:

${\omega }_1^{}=\frac{{\left(\mathrm{1,251}\pi \right)}^2}{l^2}\cdot \sqrt{\frac{EI}{\overline{m}}}.$

Which differs from the exact solution [1]:

8

${\omega }_1^2=\frac{{\left(\mathrm{1,25}\pi \right)}^2}{l^2}\cdot \sqrt{\frac{EI}{\overline{m}}}\text{by}\text{0.3 \%}\text{.}$

Thus, the solution Eq. (7) gives acceptable result.

4. Numerical investigations

Let us define the influence of the lengths and varying stiffness ratios of a stepped rod on its fundamental frequency of vibration. A steel stepped rod with different types of supports at its ends has the following parameters: span $l=$ 6 m, the smaller cross-section dimensions of the rod is $h\times b=$ 16×5 cm (second moment of area $I_x=$ 1707 cm⁴), the larger cross-section dimensions of the rod is $h\times b=$ 16×8 cm (second moment of area $I_x=$ 2731 cm⁴), elastic modulus $E=$ 2∙10⁵ MPa.

A parameter $n=$ 1707/2731 $=$ 0.625. Mass per unit length for the segment of smaller cross-section is $m_{oc}=$ 0.05∙0.16∙1∙7850 $=$ 62.8 kg/m and for the segment of larger cross-section is $m_{yc}=$ 0.08∙0.16∙1∙7850 $=$ 100.48 kg/m. The parameter $k$ is varying in such way that a plain rod with $nEI$ stiffness turns into a stepped rod with $nEI$ and $EI$ stiffness, and then into a plain rod with $EI$ stiffness. Equivalent mass of all three rods increases proportionally. The calculation is performed using the obtained Eqs. (3), (5), (7). Results of the calculation are shown in Table 1 and Fig. 4.

Fig. 4Vibration frequency curves for rods of various stiffness with various types of supports

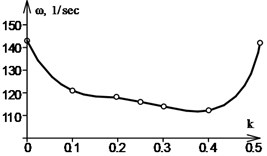
a) Fig. 1

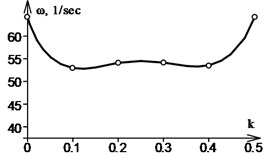
b) Fig. 2

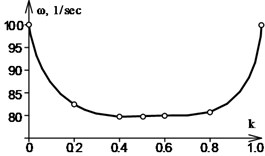
c) Fig. 3

5. Conclusions

Using the Lagrange-Ritz method, there have been obtained some approximate solutions to the problem of bending vibrations of stepped rods with various types of supports. The calculation error does not exceed 2.6 %, which is accurate enough for engineering calculations.

Numerical studies have shown the influence of the lengths and varying stiffness ratios of a stepped rod on its fundamental frequency of vibration.