Free longitudinal vibrations of functionally graded tapered axial bars by pseudospectral method

1. Introduction

Functionally graded (FG) material structures find extensive use in modern engineering as their material properties can be tailored to meet the requirements of different applications [1]. The FG axial bars are a class of inhomogeneous rods/bars with material properties varying continuously in desired spatial directions. The inhomogeneous rods are known to provide a suitable distribution of strength and weight for engineering structures [2]. A study of the vibration characteristics of these rods is a subject of considerable scientific interest that has wide applications in aerospace, civil and mechanical engineering [3-5].

The governing differential equations of motion for longitudinal vibration of non-uniform rods have variable coefficients introduced by variable cross-sectional area. In addition, for functionally graded tapered axial bars, the varying material properties add up to the previous variable coefficients in the governing equation increasing the complexity in vibration analysis of these bars/rods. In general, methods of vibration analysis are classified as analytical and numerical methods while some are semi-analytical that use a combination of both the approaches. It is generally agreed that obtaining analytical/closed-form solutions of this vibration problem is possible only for some specific geometric and material functions and are often cumbersome. Application of numerical methods becomes essential to obtain the solution of the problem for general cases. There are many different methods for the numerical solution of differential equations which include Finite Element Method (FEM), Differential Quadrature Method (DQM), Differential Transformation Method (DTM), Discrete Singular Convolution (DSC) method and Spectral/Pseudo Spectral methods. Several studies have been dedicated to the problem of exact/analytic solutions for longitudinal vibrations of non-uniform rods [6-13] while some researchers [3, 14-17] have developed numerical methods.

Eisenberger [6] obtained the exact longitudinal vibration of a rod with polynomial variation in the cross-sectional area and mass distribution along the member employing an exact element method. Bapat [7] introduced an efficient approach to solve the vibration problem of a rod composed of $N$ uniformly tapered sections and studied the vibrations of a rod composed of uniform, conical, exponential and catenoidal tapers. Abrate [8] has shown that there is a class of non-uniform rods for which the equations of motion can be transformed into the wave equation and considered area of variation of the form $A_0{\left(1+\alpha x/L\right)}^2$. Kumar and Sujith [9] obtained exact analytical solutions for the longitudinal vibration of rods with polynomial and sinusoidal area variations of form ${\left(ax+b\right)}^n$, $A_0{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left(ax+b\right).$ Li [10] carried out a functional transformation of the governing differential equation and presented the exact solutions for certain functional forms of an involved parameter. The differential transformation method was used in [11] to obtain exact solutions of the free axial vibration of a tapered bar with linearly varying mass and area. Raj and Sujith [12] derived a general analytical technique that helps in obtaining cross-sectional area variations which give specific, closed-form solutions for the longitudinal vibration of rods and have presented numerical solution for area variation of the form $x^n\exp \left(b{x}^n\right)$, $x^n\exp \left(bx\right)$. Yardimoglu and Aydin [13] obtained the exact longitudinal vibration characteristics of rods with sinusoidal area cross-sections of the form ${\mathrm{s}\mathrm{i}\mathrm{n}}^n\left(ax+b\right)$, in terms of associated Legendre functions. In [14], a domain partition power series method for the vibration analysis of variable cross-section rods is presented and the longitudinal vibrations of a rod with linearly varying area is studied. The differential quadrature method was used in [15] to analyze the free vibrations of a general non-uniform rod. In [16], the free vibration analysis of elastic rods was investigated using a novel global collocation method. An adaptive generalized finite element (GFEM) method was proposed in [17] to study the free longitudinal vibration analysis of straight bars and trusses. The results obtained using GFEM for sinusoidal and polynomial area variations of rod were compared with those obtained using finite element and composite elements methods. Several closed form solutions have been derived by the semi-inverse method for the problem of determining eigenvalues of inhomogeneous structures in [18]. It is also shown in [19] than an inhomogeneous rod can possess an exponential mode shape and derived closed-form solutions that can be utilized as model solutions for verification purposes. Recently, [3] investigated the longitudinal free vibrations of non-uniform rods by using the Discrete Singular Convolution (DSC) approach. The non-dimensional natural frequencies, obtained were compared with those obtained using exact methods and the differential quadrature method.

In most of the aforementioned works, the focus was on vibration of rods having variable area cross-sections. Recently, the longitudinal vibration of a functionally graded tapered axial bar was considered in [20] wherein, the material gradation was accounted for by varying the modulus of elasticity and mass density. Two new approaches based on Differential Transformation Method (DTM), namely Differential Transform Element Method (DTEM) and Differential Quadrature Element method of Lowest order (DQEL) were introduced by them to numerically study the free longitudinal vibration of tapered functionally graded (FG) rods. Further, in [21], the longitudinal vibrations of a $FG$ linearly tapered axial bar with exponential variation in mass density and modulus of elasticity was investigated using Finite Element Method (FEM) by proposing a new element that could be derived by using the basic principles of structural mechanics.

The purpose of this paper is to implement the pseudospectral method for the longitudinal vibration analysis of tapered $FG$ axial bars. Pseudospectral methods (PSM) are powerful tools for solving differential equations with high accuracy in a simple domain. The method has been successfully applied to the free vibration analysis of curved Timoshenko beams [22], Timoshenko beams and axisymmetric Mindlin plates [23], linear and non-linear beams [24], cylindrical helical springs [25] and Functionally graded Timoshenko beams [26]. There have been different approaches in implementing the pseudospectral formulations based on their treatment of boundary conditions. In this work, an efficient formulation of the PSM involving a change of independent variable that greatly simplifies computer programs for solving differential equations is used to transform the governing differential equation together with the boundary conditions into an eigenvalue problem, in which the eigenvalue represents the physical property of the vibration problem, namely the natural frequency. The problem is then solved using standard eigensolvers. The remainder of the paper is organized as follows. In Section 2, we introduce the pseudospectral method. In Section 3, we outline the problem and the solution methodology. In Section 4, the method is applied to examples that outline the convergence behavior, perform validations and demonstrate the advantages of the method.

2. Pseudospectral method

The spectral methods arise from the fundamental problem of approximation of a function by interpolation on an interval and are very much successful for the numerical solution of differential equations [27]. The PS method can be considered as a spectral method that performs a collocation process and delivers exponential (spectral) accuracy under the condition of smoothness. The starting point for the Pseudospectral method is the representation of the approximate solution $\left(u_N\left(x\right)\right)$ of the solution $\left(u\left(x\right)\right)$ of the given differential equation by a linear combination of basis functions $\left({\varphi }_n\left(x\right)\right),(n=\mathrm{0,1},2,\dots .,N)$:

The best choice for ${\varphi }_n\left(x\right)$ are the eigenfunctions of a singular Sturm-Liouville problem such as the Chebyshev polynomials. Although the Legendre, Hermite and Laguerre polynomials are eigenfunctions of Sturm-Liouville problem, Chebyshev polynomials are more effective in handling the boundaries [28]. The Chebyshev polynomials are recursive orthogonal polynomials that can be defined as:

where $k$ is an integer [29]. Although defined for all $x$, Chebyshev polynomials are a stable representation only on $\left(-1,1\right)$.

In PS method, one is usually content with obtaining an approximation to the solution on a discrete set of grid points. The PS method, demands that the differential equation be exactly satisfied at these set of points known as collocation points [30]. The accuracy, stability and rate of convergence of the numerical solutions depend on the choice of the collocation point [31] and the best choice for the collocation points is to use nodes that are clustered near the edges of the interval with an asymptotic density proportional to ${\left(1-x^2\right)}^{-1/2}$ as $n\to \infty$ [32]. The Chebyshev polynomial extreme points that are the Chebyshev-Gauss-Lobatto sampling grid points on $\left[-1,1\right]$ are known to have such density properties [33]. Therefore, these points are chosen as collocation points in this work. The internal points which are the extrema of $T_N\left(x\right)$ are given by:

with $i=0,N$ denoting the end points and $i=$ 1, 2, …, $N-1$ the internal points. These points correspond to:

The pseudospectral method associates the grid of collocation points with the basis set and the coefficients $a_n$ in the expansion (1) are found by requiring the residual function $L{u}_N-f$ where $L$ is the operator of the differential equation $Lu=f\left(x\right)$ to vanish at the collocation points. There are several ways of implementing the PS method of which the differentiation based formulation [34, 35], integration based formulation [36, 37] and straight forward implementation [22, 23] are normally used. The differentiation based formulation is widely used in which one can construct the differentiation matrices using the recurrence finite-differences formulae on arbitrarily spaced grids [34, 38] or utilizing the approach followed in [35, 39]. However, incorporation of boundary conditions when using differentiation matrices is complicated. The present work utilizes the straight forward implementation utilizing the Chebyshev polynomial-to-cosine change of variable together with a proper selection of internal collocation points based on the boundary conditions.

3. Mathematical formulation and solution methodology

The differential equation that governs the free longitudinal vibration of a axially graded bar reads as [40]:

Here $l$ denotes the axial coordinate, $u(l,t)$ denotes longitudinal displacement at any position $l$ and time $t$. $E\left(l\right)$, $A\left(l\right)$ and $\rho \left(l\right)$ are the modulus of elasticity, cross-sectional area and mass density respectively, which are assumed to vary along the axial coordinate $l$ with $l_1$ and $l_2$ being the end coordinates of the rod. The classical boundary conditions considered are:

The longitudinal displacement is assumed to be separable in space and time where the time dependence is harmonic with angular frequency $\omega$ i.e., $u\left(l,t\right)=W\left(l\right)e^{i\omega t}$ where $W\left(l\right)$ represents the mode shape. Denote $E\left(l\right)A\left(l\right)=S\left(l\right)$ where $S\left(l\right)$ is the axial rigidity that varies along the axial coordinate $l$.

Eq. (5) becomes $\frac{d}{dl}\left[S\left(l\right)\frac{dW}{dl}\right]=-{\omega }^2\rho \left(l\right)A\left(l\right)$:

where:

The governing equation becomes:

We now outline the solution methodology for Eq. (8) using PSM. The natural interval $x\in \left[-\mathrm{1,1}\right]$ in which the collocation points are located may be adapted to the interval of interest $l\in \left[l_1,l_1\right]$ by the transformation:

where $h=l_2-l_1$.

Due to change of variable:

Applying the transformation, the solution function $W\left(l\right)$ is now a function of $x$ and is assumed to be of the form:

Here:

It is to be noticed that the trigonometric form of the Chebyshev polynomial which is a change of coordinate is used for the representation of the approximate solution. This is coupled with analytic differentiation and collocation at internal points followed by enforcement of boundary conditions at end points.

The transformed governing differential equation is:

If we collocate Eq. (17) at the points given by Eq. (4) and enforce the boundary conditions at $\theta =$ 0, $\theta =\pi$ which are given by:

Then we get a system of equations that is expressed as a matrix eigen value equation. The resulting equation is then solved using a standard eigensolver.

4. Numerical results and discussion

In this section we examine the convergence behavior of the PS method, validate the accuracy by comparing the results obtained with other analytical/numerical methods. Finally, we apply the method to obtain the non-dimensional frequencies of vibration of a functionally graded axial bar. In all the examples considered, the rods are of unit length. The details of the work carried out in this section are presented in Table 1. A diagrammatic view of typical rods considered herein is given in Fig. 1.

4.1. Convergence behaviour of PS method

To study the convergence behaviour of the PS method in obtaining the frequency values of the vibration of non-uniform rods, some examples have been examined. As a first example, we consider the longitudinal free vibration of a fixed-free non-uniform bar with polynomial variation of cross-section area, constant elasticity modulus $E$ and constant density $\rho$ and unit length. The cross-section area varies as $A\left(x\right)=A_0{\left(1+2x\right)}^2$ where $A_0$ is a reference cross-section area. Abrate [8] has presented exact analytical solution for longitudinal free vibration of bars with polynomial area variations. The exact non-dimensional frequency parameters of rods given [8] are set as basis values and the relative error of the PS method with $N$ values varying from 10 to 16 is analyzed. The relative errors of the numerical values of the first six non-dimensional natural frequencies given by $\mathrm{\Omega }=\omega \sqrt{\rho /E}$; computed using the PS method are presented in Table 2. It is observed that the proposed method requires less number of grid points to obtain a relative error of the order of 10^-5 in the computation of the first six non-dimensional frequency values of a non-uniform rod with polynomial variation of cross section area.

As a second example we examine the convergence of the PS method by considering the free axial vibration of a tapered fixed-free bar. The area of cross-section $A\left(x\right)$ and mass density are assumed to vary linearly i.e. $A\left(x\right)=2A_{0}x$ and $m\left(x\right)=\rho \left(x\right)A\left(x\right)=2m_{0}x$ where $A_0$ is the characteristic area and $m_0$ the characteristic mass. The computations are carried out for a unit length rod. The exact first two non-dimensional frequency values given in [11] are taken as basis values and the relative error of the PS method with $N$ varying from 6 to 9 are presented in Table 3. It is observed that the present method achieves a relative error of order 10^-6 with fewer grid points.

Fig. 1A Schematic view of typical inhomogeneous rods

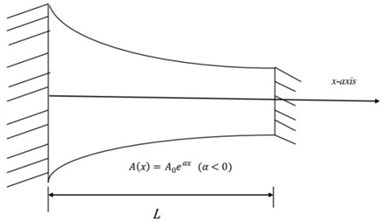
a) Fixed-Fixed non-uniform exponential rod

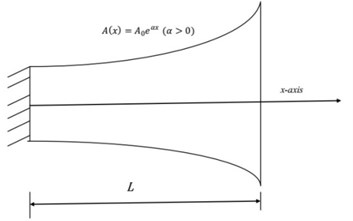
b) Fixed-Free non-uniform exponential rod

c) Fixed-Free non-uniform sinusoidal rod

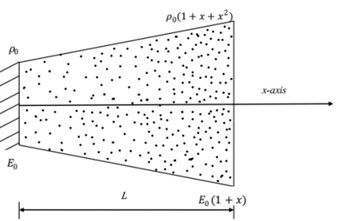
d) Side view of axially graded fixed-free bar

Table 2Convergence study of non-uniform fixed free rods with Ax=A01+2x2

Mode	Non dimensional frequency values Abrate [8]	Relative errors
		$N=$ 10	$N=$ 12	$N=$ 14	$N=$ 16
1	0.967403	3.976E-05	3.7 E-06	6.512 E-07	4.031 E-07
2	4.567452	3.027 E-06	1.860 E-07	4.816 E-08	3.721 E-08
3	7.768373	1.888 E-05	4.003 E-07	5.535 E-08	4.427 E-08
4	10.934682	6.278 E-04	3.47 E-05	1.415 E-06	9.145 E-09
5	14.089887	2.545 E-03	2.346 E-05	1.675 E-05	8.928 E-07
6	17.240109	1.525E-02	3.22 E-04	3.22 E-04	2.700 E-05

Table 3Convergence study of tapered fixed free rod with Ax=2A0x and m(x)=2m0x

Mode	Non dimensional frequency values Zang and Bert [11]	Relative errors
		$N=$ 6	$N=$ 7	$N=$ 8	$N=$ 9
1	2.4048	8.316E-05	8.316E-06	8.316E-06	8.316E-06
2	5.5201	1.105E-04	3.623 E-06	3.623 E-06	3.623 E-06

We further study the convergence of the frequency values obtained for fixed-fixed and fixed-free non-uniform rods with cross-section area given by$A\left(x\right)=x^{-0.5}\mathrm{e}\mathrm{x}\mathrm{p}(-0.5x^2)$. We examine our results with the non-dimensional frequency values presented in [3] as basis values. Using the four digit DSC results that were computed in [3] with 500 grid points for a unit length rod, the relative error of the PS method for fixed-fixed and fixed-free rods with $N$ taking values $N=$ 20, 22, 25 and 28 is presented in Table 4. The relative errors of the non-dimensional frequency parameter given by $\mathrm{\Omega }=\omega \sqrt{\rho /E}$ for the first 13 modes are given in the table. It is observed that precision of the order of 10^-5 is obtained for all the 13 modes with $N=$ 28 (29 collocation points).

5. Conclusions

The main contribution of the present study consists in applying a pseudospectral formulation for solving the governing differential equation of motion for tapered functionally graded axial bars. The method utilizes a Chebyshev polynomial-to-cosine change of variable that simplifies the computer implementation and achieves good precision. Numerical experiments that include variation in geometrical properties (area of cross-section) and/or material properties (mass density, modulus of elasticity) have been considered and the results obtained with less computational effort exhibits good accuracy and flexibility for longitudinal vibration analysis of tapered axial bars.