Free vibration analysis of tapered columns under self-weight using pseudospectral method

1. Introduction

Elastic columns are a class of important structural components that find wide applications in civil, mechanical and aerospace engineering fields [1]. The strength of an elastic column basically depends on its material and geometrical properties. The material selection and Young’s modulus determine whether a column has material non-linearity while the geometric non-linearity arises from non-uniform cross-sectional areas [2]. In conventional column vibration and buckling problems, the self-weight is often neglected and when taken into consideration, the column is referred to as a heavy column [3]. The standing heavy column is fundamental in mechanics and models tall structures and free-standing antennas [4].

Greenhill [5], using Bessel’s functions, first investigated the stability of a uniform column due to its own weight. Schafer [6] studied the effect of self-weight on the natural frequencies of a hanging cantilever beam using the Rayleigh-Ritz method. The finite element method was used by Yokoyama [7] to investigate the vibration characteristics of uniform hanging beams under gravity. Virgin et al. [8] performed analytical and experimental studies on the effect of gravity on the vibration of vertical cantilevers. Duan and Wang [3] presented analytical solutions for the buckling of columns including self-weight. Okay et al. [9] applied the variational iteration method to determine the buckling loads and mode shapes of heavy columns under its own weight. An analytic method involving the Fredholm integration method was used by Huan and Li [10] to analyze the buckling behavior of axially nonuniform graded columns. The differential quadrature (DQ) method was used by Mahmoud et al [11] to investigate the effect of column geometry on the natural frequencies and mode shapes. Taha and Essam [12] used the DQ method to study the stability behavior and free vibration of axially loaded tapered columns with elastic end restraints. Recently, Wang [13] used a numerical initial value method to study the influence of gravity as well as taper on the vibration of a standing column.

Although many methods have been presented to analyze problems concerned with taper and self-weight, most of them apply to specific cases determined by the form of the equations. This study presents a simple numerical technique that is capable of handling different cases using the pseudospectral formulation. In terms of effective mathematical techniques, Pesudospectral (PS) methods have been used in recent years for structural engineering analysis. Lee and Schultz [14] applied the Chebyshev PS method to solve the vibration of Timoshenko beams and Mindlin plates. Yagci et al. [15] used a spectral Chebyshev technique for solving linear and nonlinear beam equations. Sari and Butcher [16] used the PS method for the free vibration analyses of non-rotating and rotating Timoshenko beams with damaged boundaries. In [17], the PS method is used to investigate the dynamic response of Timoshenko beams made of functionally graded materials. A Chebyshev PS method is presented in [18] for the static analysis of the geometrically exact beams undergoing large deflections. However, to the author’s knowledge no analytical solution exists for the important problem of the vibration of a standing heavy tapered column. A numerical initial value method proposed in [13] that combines the initial value method [19] with Runge-Kutta method and bisection method is the only available technique present in literature. The important problem demands techniques that are easy to implement and computationally inexpensive.

The intention of this work is to explore the application of a novel formulation of the Chebyshev Pseudospectral method to the vibration analysis of heavy and tapered columns. The method is first validated by computing the frequencies of vibration of non-uniform beams where their density and the flexural rigidity vary along the longitudinal axis. The influence of gravity, taper and gravity and taper on the vibrations of columns is then analyzed and the results are compared with those obtained using exact solutions [20], a Differential Quadrature Method [11] and a numerical initial value method [13].

2. Equations

The vibration of long and slender beams/columns is an important problem in applied mechanics and are generally modeled by the Euler-Bernoulli beam theory [21]. Assuming the effects of rotational inertia and transverse shear deformation to be negligible, the equation for small vibrations of a non-uniform Euler Bernoulli column subjected to an axial force $F$ is given by [13]:

where $\left(x,y\right)$ are the longitudinal and transverse coordinates of the column with the origin at the base, $EI$ is the flexural rigidity, $\rho$ is the mass per length and $t$ is the time. For a standing column of height $L$, axial force is given by:

where $g$ is the acceleration due to gravity. Introducing $y\left(x,t\right)=w\left(x\right)e^{ikt}$, $EI\left(x\right)=E{I}_{o}l\left(x\right)$, $\rho \left(x\right)={\rho }_{o}r\left(x\right)$, where $E{I}_o$ and ${\rho }_o$ are the maximum values of flexural rigidity and mass per length occurring at the base $x=0$ and $k$ is the frequency of vibration. Normalizing all length by $L$ Eq. (1), becomes:

where $\omega =k{L}^2\sqrt{{\rho }_o/E{I}_o}$ and $\beta =g{\rho }_o{L}^3/E{I}_o$.

Eq. (3) does not have a closed form solution even for a uniform beam/column [21]. Assuming that the column has linear taper with the rigidity and density varying as $l\left(x\right)={\left(1-cx\right)}^m$, $r\left(x\right)={\left(1-cx\right)}^n$ where $m$, $n$ are positive constants and $0\le c\le 1$ representing the degree of taper, Eq. (3) becomes:

where:

For clamped-free (C-F) columns with clamped end $x=0$ and free end $x=$ 1, the boundary conditions can be written as:

If $c=$ 0, the column is uniform and for $c=$ 1, the column has a pointy tip.

For $c\ne$ 1, Eq. (6) reduces to:

Eq. (4) is solved subject to the boundary conditions given by Eq. (5) and Eq. (6) for different values of $m$, $n$. Though the equations can be solved for general values of $m$, $n$, we consider some special cases which correspond to those shown in Fig. 1. In the case of a solid tapered column of circular cross section, $m=$4, $n=$2, while for a solid column of constant thickness and tapered sides $m=$1, $n=$1 or $m=$ 3, $n=$1. If the column vibrates about the axis A-A which is perpendicular to the thickness direction $m=$1, $n=$1 and if the column vibrates about the axis B-B which is parallel to the thickness direction $m=$3, $n=$1 [13].

Fig. 1a) Tapered column of circular cross section, b) solid column of constant thickness and tapered sides

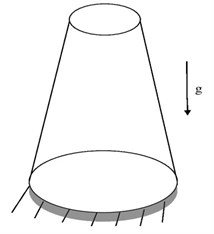
a)

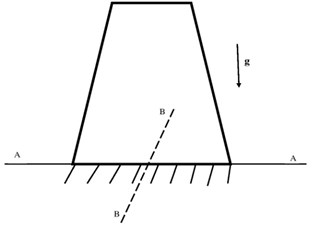
b)

3. Numerical results and discussion

In this section, we study the convergence behavior of the PS method first and then consider some numerical examples to validate the efficiency of the Pseudospectral method. The first numerical example is devoted to a beam with constant thickness and linearly tapered width with clamped base and no tip mass. The second is concerned with the vibration of a hanging uniform column under self-weight. The third example considers the free vibration of non-uniform column with no self-weight. The last example concerns the influence of gravity and taper on the vibration of a standing column.

4. Conclusions

Typically, the free vibration frequencies of a non-uniform gravity loaded Euler-Bernoulli column/beam is obtained numerically as the governing fourth order differential equation with variable coefficients does not yield any closed form solutions. The numerical technique-Chebyshev Pseudospectral method explored in this paper introduces a novel formulation of the method in which the basis functions and their derivatives are computed using trigonometric functions. The stability of the method is first studied by obtaining the vibration frequencies of a linearly tapered beam in the absence of gravity. The accuracy of the method is further tested against the exact solutions of a class of non-uniform beams in the absence of gravity, solutions obtained using two variants of DQM for a non-uniform column under different end conditions and also against the solutions obtained using an initial value method in the case of a uniform column under self-weight. Finally, the proposed method is used to find the vibration frequencies of a standing linearly tapered heavy column. A comparison of the results obtained with those of the numerical initial value method shows that the proposed technique is an efficient and reliable method in handling vibration columns of elastic columns/beams. It is also possible to extend the technique to other tapers and consider inclusion of shear effects as in a Timoshenko column.