Abstract
Results of experimental investigations of vibrations of a circular plate under impact loading are presented. In such structures when there are small defects causing non-symmetry, such as Braille elements, transient beating phenomenon is observed. Simplified mathematical model for the investigation of this experimentally determined transient beating phenomenon is proposed and numerical results based on this model are obtained and investigated. From the presented results qualities of the envelope function in the investigated transient beating phenomenon are determined.
1. Introduction
Results of experimental investigations of vibrations of a circular plate under impact loading are presented. From the performed experimental investigation, it was determined that in such structures, when there are small defects causing non-symmetry, such as Braille elements, transient beating phenomenon is observed.
Simplified mathematical model for the investigation of this experimentally determined transient beating phenomenon is proposed. The model is based on the modal equations for two almost multiple eigenmodes. Using as the basis this mathematical model numerical results are obtained and investigated. From the presented results qualities of the envelope function in the investigated transient beating phenomenon are determined.
The structure of the paper is the following one:
1) Experimental results are presented, from the results of measurement at some of the points of the structure transient beating phenomenon is observed.
2) Simplified mathematical model of the transient beating phenomenon, which was obtained in some of the measurement points of the previously described experimental investigation, is proposed and described.
3) Results of numerical investigations using this mathematical model are presented in detail and their qualities, that is qualities of the envelope function of transient vibrations, are discussed.
Numerical model for transient beating phenomenon investigated in this paper is based on equations for eigenmodes presented in [1]. Modal decomposition of equations describing dynamics of linear elastic systems is also described in [2]. Basic material for solution of problems of this type is also presented in [3]. Beating phenomenon in the interpretation of experimental moiré images is investigated in [4]. Contemporary methods of investigation of dynamics of vibrating systems are described in [5]. Basic problems of vibrations and their investigations are presented in [6]. Mechanical vibrations and their analysis are described in [7]. Basics of processes of vibrations and their engineering applications are presented in [8]. Numerical procedures for investigation of dynamics of nonlinear systems are described in [9]. Applied procedures of numerical analysis are presented in [10]. Investigations of approximations in numerical calculations are presented in [11]. Bending analysis of laminated sector plates with polar and rectilinear orthotropy is performed in [12]. Buckling of orthotropic plates under in-plane loading is investigated in [13]. Analysis of bending of sector plates by contemporary numerical methods is described in [14]. Friction between finger skin and material surfaces is investigated in [15]. Physical relationships for paper and other similar materials are presented in [16]. Investigations of longitudinal vibrations of the rollers in a folding machine are performed in [17]. Vibrations of rotating elements in a folding machine are investigated in [18]. Effect of dynamic regime of rollers of pocket folding machine to quality of printing products is analyzed in [19]. Technical characteristics of laser displacement measurement head “Microtrack LTC 200-100” are given in [20]. Analysis of creasing and folding of paperboards is performed in [21]. Polymer film packaging for food and other products is investigated in [22]. New materials for packaging based on multilayer films are described in [23]. In-plane vibrations using time averaged stochastic moiré are investigated in [24]. Analysis of multilayer materials by moiré interferometry is described in [25]. Investigations of vibrations using time averaged shadow moiré are presented in [26]. As a fundamental book on time averaged moiré fringes [27] can be recommended. Experimental methods for two dimensional elastic structures are presented in [28]. Computer processing of experimental images is described in [29]. Basic book on the experimental method of holographic interferometry is [30].
The obtained results are used in the process of investigation of decay of vibrations of elements of symmetric structures with Braille elements.
The purpose of this paper is to propose a mathematical model for beating phenomenon in transient processes and to present experimental as well as numerical investigations of this phenomenon.
2. Experimental setup for the analysis of vibrations and transient beating phenomenon
For qualitative estimation of vibrations of the investigated structure the vibrometer Polytec PSV – 500 was used. Schematic representation of the experimental setup is shown in Fig. 1.
Fig. 1Schematic representation of the experimental setup: 1 – exciter of vibrations (shaker), 2 – the investigated object, 3 – scanning heads Polytec PSV – 500, 4 – vibrometer Polytec PSV – 500, 5 – personal computer
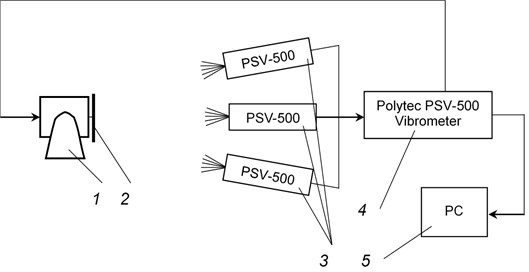
This experimental setup enabled to register vibrations in transient processes and to determine the transient beating phenomenon described further. One is to note high precision of the experimental procedure of registration of transient vibrations using this type of experimental setup.
3. Experimental investigations of decay of vibrations and transient beating phenomenon
Circular plate under impact loading is investigated. Results of investigation of vibrations for various measurement points are presented in Fig. 2.
Fig. 2Experimental results of decay of vibrations for various measurement points
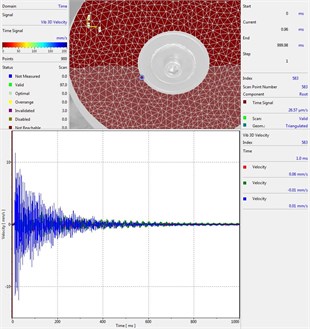
a) Measurement point number 1
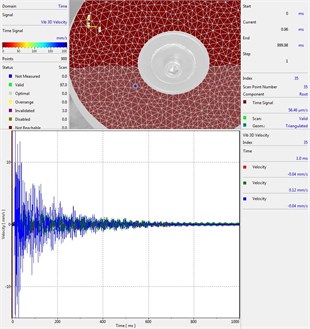
b) Measurement point number 2
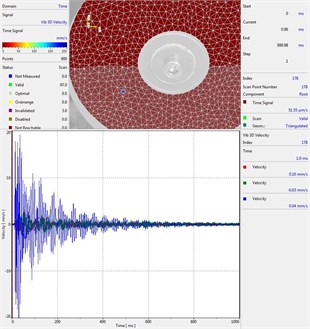
c) Measurement point number 3
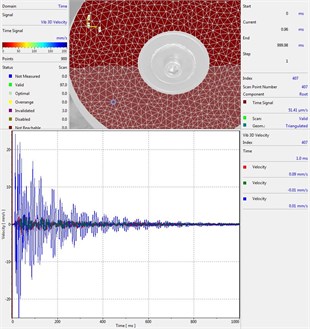
d) Measurement point number 4
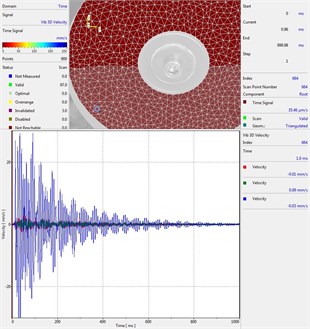
e) Measurement point number 5
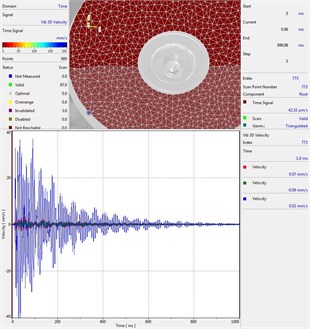
f) Measurement point number 6
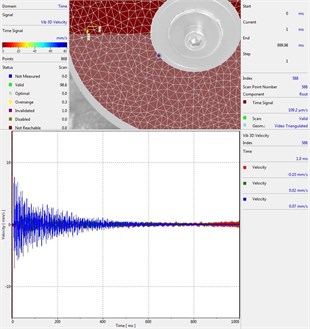
g) Measurement point number 7
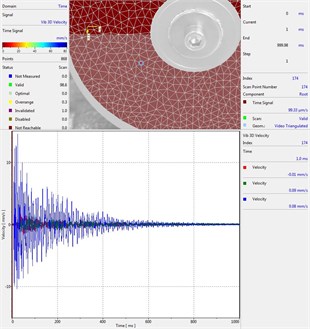
h) Measurement point number 8
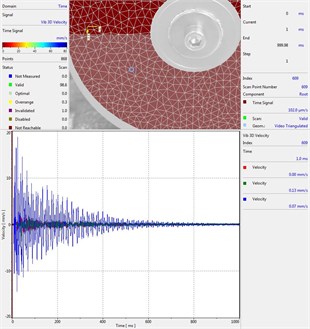
i) Measurement point number 9
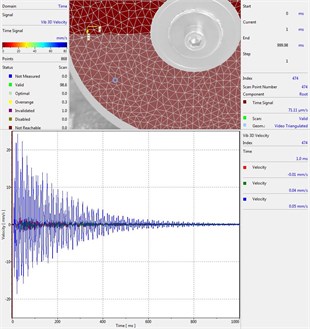
j) Measurement point number 10
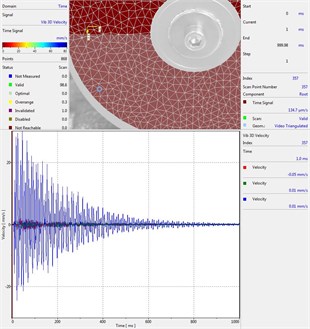
k) Measurement point number 11
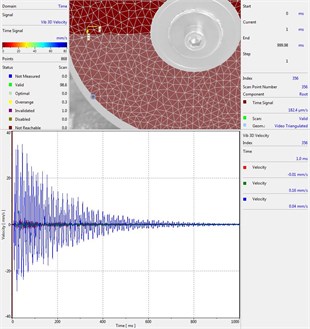
l) Measurement point number 12
From the presented results decay of vibrations is clearly seen. In some of the presented results transient beating phenomenon is observed, which is caused by small defects such as Braille elements.
By transient beating phenomena in this investigation is assumed the behavior of the decaying envelope function of lower frequency than the observed high frequency vibrations. As seen from the presented experimental results this phenomenon is clearly seen in only some of the measurement points of the structure, while in some of the points it is not so clearly seen. Using the presented experimental results as the basis it is determined that the results of measurements substantially depend on the location of the measurement points.
Further the simplified mathematical model for this experimentally observed transient beating phenomenon is proposed and numerical investigations are performed.
4. Mathematical model for the numerical investigation of transient beating phenomenon
It is assumed that two eigenmodes of the structure are excited. Modal equations for free motion have the form:
where are the coefficients of the eigenmodes, are the eigenfrequencies, are the modal damping coefficients, upper dot denotes differentiation with respect to time and the number of the eigenmode:
It is assumed that both eigenmodes equally contribute to the resulting displacement , that is:
The following initial conditions are assumed in the investigation presented further:
and:
The following values of modal damping coefficients are assumed in the investigation presented further:
The first eigenfrequency is assumed to be given by the following relationship:
and the second eigenfrequency is assumed to be given by the following relationship:
where denotes the parameter of the investigated model. In the investigation presented further it is assumed that has the numerical values given by the following equation:
In the investigation presented further it was assumed that the parameter of the investigated problem is:
Further results of numerical investigations of the proposed mathematical model for transient beating phenomenon are presented.
5. Results of numerical investigation of mathematical model for transient beating phenomenon
Results of numerical calculation of displacement as a function of time for various values of 1, 2, …, 16 were obtained and investigated. Some of the obtained results are presented in Fig. 3.
Fig. 3Displacement as a function of time for various values of difference of eigenfrequencies
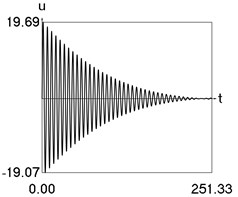
a) 2
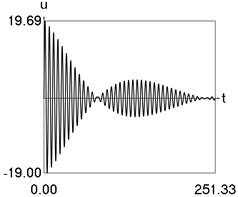
b) 4
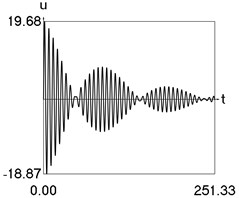
c) 6
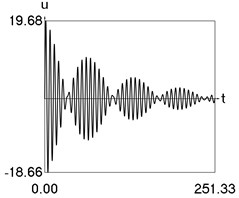
d) 8
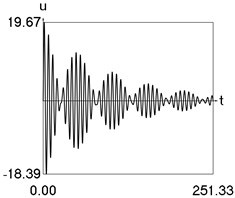
e) 10
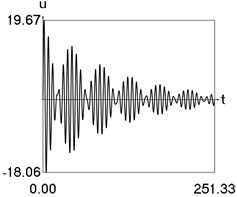
f) 12
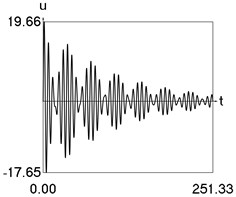
g) 14
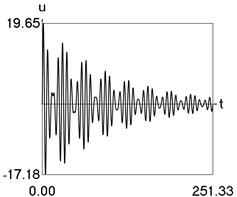
h) 16
From the performed investigations it was determined that the period of the envelope function decreases when the difference of the eigenfrequencies increases. In Fig. 3(a) the envelope function has no peaks in the investigated interval, in Fig. 3(b) the envelope function has one peak in the investigated interval, in Fig. 3(c) the envelope function has two peaks in the investigated interval, in Fig. 3(d) the envelope function has three peaks in the investigated interval, in Fig. 3(e) the envelope function has four peaks in the investigated interval, in Fig. 3(f) the envelope function has five peaks in the investigated interval, in Fig. 3(g) the envelope function has six peaks in the investigated interval, in Fig. 3(h) the envelope function has seven peaks in the investigated interval.
The envelope function for a different problem with beating phenomenon was investigated in the earlier paper [4] and it was expressed by using the zero order Bessel function of the first kind In this problem the envelope function is given by the transient zero order Bessel function of the first kind Properties of this envelope function are seen from the presented graphical results.
The main conclusion is that the period of the decaying envelope function decreases with the increase of the difference between the two almost multiple eigenfrequencies. This difference of almost multiple eigenfrequencies is caused by Braille element or some other type of small defect of the structure.
All authors declare that all of them have made contributions to the paper. On this basis contributions of all coauthors are acknowledged.
6. Conclusions
Results of experimental investigations of vibrations of a circular plate under impact loading are presented. In such structures when there are small defects causing non-symmetry, such as Braille elements, transient beating phenomenon is observed.
Simplified mathematical model for the investigation of transient beating phenomenon previously observed in the experimental investigations is proposed and numerical results are obtained and investigated. From the performed investigations it was determined that the period of the envelope decreases when the difference of the eigenfrequencies increases. The envelope function for different problem investigated in the earlier paper was expressed by using the zero order Bessel function of the first kind . In this problem the envelope function is given by the transient zero order Bessel function of the first kind . Properties of this transient zero order Bessel function of the first kind, representing the envelope function, are seen from the presented graphical results.
As presented above in this paper a mathematical model for beating phenomenon in transient processes is proposed and experimental as well as numerical investigations of this phenomenon are performed.
The obtained experimental as well as numerical results are used in the process of investigation of decay of vibrations of elements of printing devices and symmetric structures with Braille elements.
References
-
Zienkiewicz O. C. The Finite Element Method in Engineering Science. Mir, Moscow, 1975, (in Russian).
-
Bathe K. J. Finite Element Procedures in Engineering Analysis. Prentice-Hall, New Jersey, 1982.
-
Bathe K. J., Wilson E. L. Numerical Methods in Finite Element Analysis. Stroiizdat, Moscow, 1982, (in Russian).
-
Ragulskis M., Maskeliūnas R., Ragulskis L., Turla V. Investigation of dynamic displacements of lithographic press rubber roller by time average geometric moire. Optics and Lasers in Engineering, Vol. 43, 2005, p. 951-962.
-
Inman D. J. Vibration with Control, Measurement, and Stability. Prentice-Hall, New Jersey, 1989.
-
Bolotin V. V. Vibrations in Engineering. Handbook, Vol. 1, Mashinostroienie, Moscow, 1978, (in Russian).
-
Lalanne M., Berthier P., Der Hagopian J. Mechanical Vibrations for Engineers. John Wiley and Sons, New York, 1984.
-
Thomson W. T. Theory of Vibration with Applications. Prentice-Hall, New Jersey, 1981.
-
Levy S., Wilkinson J. P. D. The Component Element Method in Dynamics with Application to Earthquake and Vehicle Engineering. McGraw-Hill, New York, 1976.
-
Segerlind L. J. Applied Finite Element Analysis. Mir, Moscow, 1979, (in Russian).
-
Zienkiewicz O. C., Morgan K. Finite Elements and Approximation. Mir, Moscow, 1986, (in Russian).
-
Maleki S., Tahan M. Bending analysis of laminated sector plates with polar and rectilinear orthotropy. European Journal of Mechanics A – Solids, Vol. 40, 2013, p. 84-96.
-
Farajpour A., Shahidi A. R., Mohammadi M., Mahzoon M. Buckling of orthotropic micro/nanoscale plates under linearly varying in-plane load via nonlocal continuum mechanics. Composite Structures, Vol. 94, Issue 5, 2012, p. 1605-1615.
-
Fereidoon A., Mohyeddin A., Sheikhi M., Rahmani H. Bending analysis of functionally graded annular sector plates by extended Kantorovich method. Composites Part B – Engineering, Vol. 43, Issue 5, 2012, p. 2172-2179.
-
Kim M. S., Young Kim I., Kyu Park Y., Ze Lee Y. The friction measurement between finger skin and material surfaces. Wear, Vol. 301, 2013, p. 338-342.
-
Castro J., Ostoja-Starzewski M. Elasto – plasticity of paper. International Journal of Plasticity, Vol. 19, 2003, p. 2083-2098.
-
Kibirkštis E., Miliūnas V., Havenko S., Ragulskis K., Ragulskis L. Measurement of longitudinal vibrations of the rollers in a folding machine. Journal of Measurements in Engineering, Vol. 5, Issue 1, 2017, p. 40-48.
-
Ragulskis K., Ragulskis L., Kibirkštis E., Augutis S. V., Vainilavičius D., Miliūnas V., Pauliukaitis D. Measurement of vibrations of rotating elements in a folding machine. Journal of Measurements in Engineering, Vol. 3, Issue 1, 2015, p. 9-16.
-
Kibirkštis E., Augutis S. V., Vainilavičius D., Miliūnas V., Pauliukaitis D., Ragulskis L. Effect of dynamic regime of rollers of pocket folding machine to quality of printing products. Journal of Vibroengineering, Vol. 17, Issue 6, 2015, p. 2869-2881.
-
Technical Characteristics of Laser Displacement Measurement Head “Microtrack LTC 200-100”. http://mtiinstruments.com/pdf/products/microtrak2sal.pdf.
-
Huang H., Hagman A., Nygards M. Quasi static analysis of creasing and folding for three paperboards. Mechanics of Materials, Vol. 69, Issue 1, 2014, p. 11-34.
-
Barlow C. Y., Morgan D. C. Polymer film packaging for food: an environmental assessment. Resource Conservation and Recycling, Vol. 78, 2013, p. 74-80.
-
Tartakowski Z. Recycling of packaging multilayer films: new materials for technical products. Resource Conservation and Recycling, Vol. 55, 2010, p. 167-170.
-
Ragulskis M., Maskeliūnas R., Saunorienė L. Identification of in-plane vibrations using time average stochastic moire. Experimental Techniques, Vol. 29, 2005, p. 41-45.
-
Han L., Voloshin A., Emri I. Study of the multilayer PCB CTEs by moiré interferometry. Optics and Lasers in Engineering, Vol. 42, 2004, p. 613-626.
-
Ragulskis K., Maskeliūnas R., Zubavičius L. Analysis of structural vibrations using time averaged shadow moire. Journal of Vibroengineering, Vol. 8, Issue 3, 2006, p. 26-29.
-
Saunorienė L., Ragulskis M. Time – Averaged Moire Fringes. Lambert Academic Publishing, 2010.
-
Timoshenko S. P., Goodier J. N. Theory of Elasticity. Nauka, Moscow, 1975, (in Russian).
-
Soifer V. A. Computer processing of images. Herald of the Russian Academy of Sciences, Vol. 71, Issue 2, 2001, p. 119-129, (in Russian).
-
Vest C. Holographic Interferometry. Mir, Moscow, 1982, (in Russian).
About this article
This research was supported by Lehigh University (USA) and Kaunas University of Technology (Lithuania) Memorandum of Understanding to collaborate on a Project “Development of Novel Optical Methods for Defectoscopy of Polymer Films for Polygraphic and Packaging Manufacturing” (Partnership Agreement No. F4-90-87, 15 May 2013).
