Abstract
Aiming at the characteristics of high speed water entry of heavy projectiles, this article studied the high-speed water impact load of heavy projectiles by the multi-material ALE method, good agreements were obtained compared with the empirical formula, then analyzed the two parameters of impact velocity and the projectile’s mass which will affect the impact load when changed. Numerical simulation results are as follows: under vertical water entry condition, the acceleration of the projectile is roughly proportional to the square of the impact velocity and inversely proportional to the projectile’s mass during water impact.
1. Introduction
The problem of water entry has been widely concerned for a long time. Research on the water entry phenomena has been motivated by an interest in the load during water impact [1-3], the shape of cavity [4] and the generation and propagation of the ballistic waves into the fluid [5, 6]. In recent years, with the development of the finite element method (FEM), more and more researchers have begun to use finite element method to solve the problem of water impact aiming at a specific condition. Wang Jian investigated the phenomenon of the rocket sled water-brake high speed water entry by using the method of fluid-solid coupling. The modalities of water were calculated such as super-cavitations, uplift, spatter and pressure, and the velocity, deceleration and resistance coefficient varied with time of water-brake was obtained [7]. Ma Qingpeng studied the multiphase flow and the movement of a cylinder body with a cone head by using the method of volume of fluid (VOF) and dynamic mesh. The velocity attenuation and induced cavity shape were obtained with an initial velocity of 500 m/s. Good agreements were obtained compared with the theoretical results [8].
Investigations on the high-speed water entry of small projectiles (with a diameter of 1 cm-5 cm) are relatively mature [8-10]. Due to the limitation of experimental conditions, only a few researches have investigated the water-impact of super heavy projectiles (with a diameter of 40 cm-60 cm) at a relatively low speed (40 m/s-100 m/s) [11, 12]. While the investigation of high speed (200 m/s-300 m/s) water entry of heavy projectiles (with a diameter of 10 cm-40 cm) is relatively rare. The method of multi-material ALE is used in this paper to investigate the impact load of high speed water entry of hemispherical-nosed heavy projectiles.
2. Numerical simulation
High speed water entry involving the flow of three phases contains fluid, water and solid. Multi-material ALE (Arbitrary Lagrangian Eulerian) method is good at investigated it numerically.
ALE method includes mass, momentum and energy conservation equations are as follows [7]:
where is the fluid density, is the fluid velocity, is the hydrodynamic viscosity coefficient. is the convection velocity, is the Euler coordinate value, is the stress strain, is the body force, is the total specific energy.
The eight-node hexahedron element is used in the model. The fluid grids are defined as ALE with the material of NULL. The water’s EOS (equation of state) is Gruneisen and the air’s EOS is Linear-polynomial. The solid grids are defined as Lagrangian and the material of the projectile is common structural steel. The projectile was in the air at the initial time. Cause of the symmetry of the model, the water-entry model can be simplified as a quarter models in order to reduce the work of computation. The numerical simulation model is as illustrated in Fig. 1.
The profiles are defined as symmetry planes and the rest of surfaces are defined as none-reflect boundaries in order to simulate the unlimited-surroundings. Using level set method to tracking the interface of water and air and using operator splitting method to solve the fluid solid coupling problem.
Set the hemispherical-nosed heavy projectile’s diameter is 40 cm, height is 120 cm and weight is 171 kg, with an initial velocity of 200 m/s from a height of 0.1 m above the liquid surface, then the cavity formed during the water entry simulated numerically are shown as Fig. 2 and the curve of the projectile’s acceleration, which represents the impact load, with time is shown as Fig. 3.
Fig. 1Model of projectile’s water-entry vertically
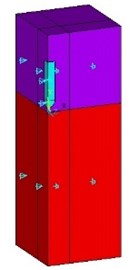
Fig. 2Cavity formed during the water entry
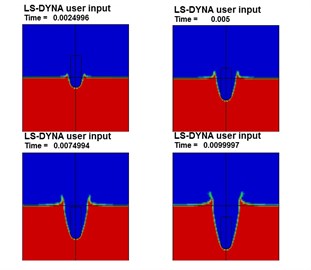
Fig. 3Projectile’s acceleration curve during water entry
During the water entry, the surface water surrounds the cavity is uplifted. A spindly huge cavity formed behind the projectile’s nose.
The projectile’s acceleration is relatively high during the water impact, and then the projectile’s acceleration maintains a relatively stable value after the impact cause that the penetration velocity maintains a relatively stable value during the short time.
3. Contrasting analytical and numerical results
During the water impact, the projectile’s velocity can be considered as a constant, May A. considers the cavity formed during early water entry can be approximated as a parabola except the area near the projectile’s nose. Theoretical predictions and experimental measurements predicted that the shape of the cavity can be expressed as below [13]:
where is the projectile’s diameter, is the drag coefficient of a cavitation vehicle, for spheres, the correlation of the drag coefficient shows that there are ranges classified by velocity, roughly “subsonic” up to 0.5, 0.384 [4].
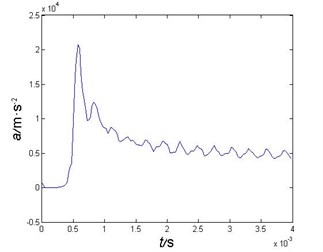
In order to keep the projectile’s velocity stable during water impact, here set the projectile’s weight as 740 kg. Comparisons of the cavity formed during water entry by the heavy projectile are shown as Fig. 4, which showed that numerical results have a good agreement with the analytical results, then the validity of the simulation model is verified.
Fig. 4Comparisons of the cavities formed during the water entry
4. Influence of changing two parameters on the impact load
From the investigation above, it can be concluded that the maximum value of projectile’s load appears during the early stage (within 0.2 ms after touching the water surface) of water entry. This paper also numerically calculated the acceleration curve during water entry of the projectile with impact velocities of 240 m/s, 280 m/s and 320 m/s, and the comparison of the acceleration curve are shown as Fig. 5, the comparison of the peak acceleration under different impact velocity is as Table 1.
Table 1Different impact velocities and corresponding peak acceleration
(m/s) | (104m/s2) | (m-1) |
200 | 2.07 | 0.52 |
240 | 3.04 | 0.53 |
280 | 4.11 | 0.52 |
320 | 5.13 | 0.50 |
It can be concluded that the maximum value of the projectile’s acceleration is roughly proportional to the square of the impact velocity.
In order to investigate the difference of different mass projectiles’ impact load, this paper also numerically calculated the acceleration during water entry of the projectiles with different mass of 142 kg, 171 kg, 199 kg and 228 kg, and the comparison of the acceleration curve are shown as Fig. 6, the comparison of the peak acceleration is shown as Table 2.
A conclusion can be derived from Fig. 6 and Table 2 that projectiles’ acceleration is roughly inversely proportional to the projectile’s mass during the water impact.
Fig. 5Comparison of projectile’s acceleration curves
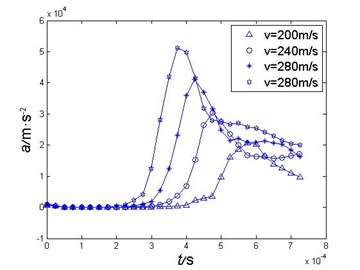
Fig. 6Comparisons of different mass projectiles’ acceleration curves
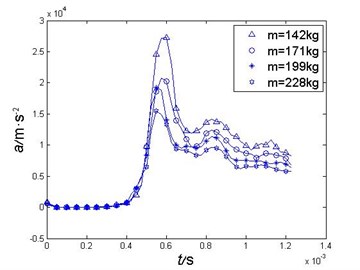
Table 2The mass of each projectile and its corresponding peak acceleration
(kg) | (104m/s2) | (106N) |
142 | 2.27 | 3.2 |
171 | 2.07 | 3.5 |
199 | 1.92 | 3.8 |
228 | 1.55 | 3.5 |
5. Conclusions
This article studied the high-speed water entry phenomena of heavy projectiles by the multi-material ALE method, good agreements were obtained compared with the empirical formula. By changing the parameters of simulation conditions, two conclusions have been obtained.
1) The maximum value of the projectile’s acceleration is proportional to the square of the impact velocity, and the duration time of maximum acceleration will decrease with the increasing of the impact velocities.
2) The maximum value of the projectile’s acceleration is roughly inversely proportional to the projectile’s mass during the water impact.
References
-
Vonkarman T. The Impact of Seaplane Floats during Landing. National Advisory Committee for Aeronautics, NACA Technical Notes 321, Washington, 1929.
-
Wagner V. H. Phenomena associated with impacts and sliding on liquid surfaces. ZAMM – Journal of Applied Mathematics and Mechanics, Vol. 12, Issue 4, 1932, p. 193-215.
-
Egorov I. T. Impact on a Compressible Fluid. NACA 1413, Washington, 1956.
-
Lee M., Longoria R. G., Wilson D. E. Cavity dynamics in high-speed water entry. Physics of Fluids, Vol. 9, Issue 3, 1997, p. 540-550.
-
Korobkin A. A., Peregrine D. H. The energy distribution resulting from an impact on a floating body. Journal of Sound and Vibration, Vol. 229, Issue 3, 2000, p. 579-605.
-
Weidong Peng, Peregrine D. H. Pressure-impulse theory for plate impact on water surface. The 15th International Workshop on Water Waves and Floating Bodies, Caesarea, 2000.
-
Wang Jian, Zhao Qing Bin, Tao Gang, Wu Jun Ji Numerical simulation on rocket sled water-brake high-speed water-entry impact. Explosion and Shock Waves, Vol. 30, Issue 6, 2010, p. 628-632.
-
Ma Qingpeng, Wei Yingjie, Wang Cong, Cao Wei Numerical simulation of high-speed water entry cavity of cone cylinder. Journal of Beijing University of Aeronautics and Astronautics, Vol. 40, Issue 2, 2014, p. 204-209, (in Chinese).
-
Zitao Guo, Wei Zhang, Xinke Xiao, Gang Wei, Peng Ren An investigation into horizontal water entry behaviors of projectiles with different nose shapes. International Journal of Impact Engineering, Vol. 49, 2012, p. 43-60.
-
Wei Zhuo Hui, Wang Shu Shan, Ma Feng Diving impact load of rigid truncated conical projectile. Acta Armamentarii, Vol. 31, Issue 1, 2010, p. 118-120, (in Chinese).
-
Zhang Yue Qing, Cai Wei Jun, Li Jian Chen, Wang Zhi Jie Application of a FEM/SPH coupling method to torpedo water entry. Torpedo Technology, Vol. 25, Issue 1, 2017, p. 1-6, (in Chinese).
-
Pan Guang, Wei Gang, Du Xiao Xu The design and simulation of water entry and underwater trajectory for airdropped mine. Fire Control and Command Control, Vol. 32, Issue 3, 2007, p. 85-93, (in Chinese).
-
May A. Water Entry and the Cavity-Running Behavior of Missiles ADA020429. White Oak Laboratory, Maryland, 1975.
