Path planning of mobile robot based on hybrid improved artificial fish swarm algorithm

1. Introduction

With the rapid development of robot technology, mobile service robots are increasingly appearing in people’s daily life. As one of the important manifestations of intelligent mobile robot, autonomous path planning has become the focus of research in the field of robotics, the goal is that the robot moves the robot from the initial position to the target position according to the optimal path or the target (for example, the minimum energy consumption, the better path smoothness, the shortest completion time, etc.), and the movement process To avoid collisions with any obstructions in the environment [1]. At present, there are many algorithms for path planning, such as genetic algorithm, ant colony algorithm, particle swarm algorithm, neural network algorithm [2]. In the natural world, the fish can find the highest food content in the waters according to the behavior of other fish. By analyzing the characteristics of the real fish, the researchers proposed the artificial fish swarm algorithm to construct the artificial fish to simulate the rear tail of the real fish. Group and foraging and other biological behavior activities, the use of bottom-up optimization model to achieve the overall optimization within the work space.

Dr. Li Xiaolei first proposed the algorithm in 2003, and later found that the artificial fish swarm algorithm has strong robustness and fast convergence [3]. The advantages are applicable to the path planning of robots. Peng, Jiansheng maps the path planning to the mathematical model TSP (Traveling Salesman Problem) to improve the detection method of foraging behavior in artificial fish swarm algorithm and improve the convergence efficiency of the algorithm [4]. Wang, Jian et al. Proposed an adaptive behavior-based artificial fish swarm algorithm that ignores the crowding factor and applies it to the robot path planning. Li, Guangqiang et al. Grouped the population into two subgroups of the same size, and applied different adaptation strategies to two groups, one to focus on the global search and the other on the local search [5]. The convergence efficiency and optimization accuracy of the algorithm. Fei, Teng et al. Proposed an improved artificial fish swarm algorithm based on DNA calculation, introducing DNA crossover and DNA mutation operation to improve the slow convergence rate of artificial fish swarm algorithm [6]. Zhang, Chao et al. Proposed an improved artificial fish swarm algorithm to improve the convergence of the algorithm by dynamically adjusting the field of view and step size of artificial fish [7]. The improved artificial fish swarm algorithm proposed above has been effective in improving the convergence and precision of the algorithm, but not taking into account the impact of the size of the artificial fish size on the algorithm and the problem of the global planning and local planning balance of the artificial fish swarm algorithm. The adaptive behavior based on the nonlinear inertia weighting factor $\omega$ is proposed. The attenuation function $\alpha$ is used to dynamically adjust the field of view and the moving step size of the artificial fish, the global optimization and local optimization of the equilibrium algorithm and improve the convergence speed and accuracy of the algorithm.

2. Hybrid improvement algorithm description

In AFSA, when the artificial fish population is too large, the algorithm takes a large amount of computation and takes up more storage space. When the fish population is too small, the fish are locally optimized, premature, and easy to fall into the local extreme. In this paper, A* Algorithm [8] to plan out the second-best path, through the second-best path to determine the available vectors and coordinate points, and then through these different combinations of coordinate points to determine the size of the artificial fish algorithm in the artificial fish. A hybrid improved Artificial Fish Swarm Algorithm (HIAFSA) is proposed. Firstly, the sub-optimal path is determined by A* algorithm, and then the adaptive behavior of artificial fish swarm algorithm is improved based on the inertia weight factor, and the attenuation function $\alpha$ is introduced to improve the visual range and moving step length of the artificial fish, balance the global path planning and local path planning.

2.2. Hybrid algorithm implementation process

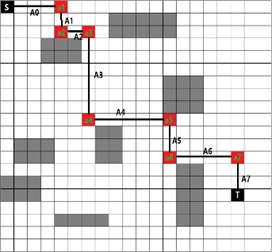
To establish a grid map model, as shown in Fig. 2, a 20×20 grid map [9], where the black point S(0,0) is the starting point of the mobile robot, the point T(18,15) is the end point;

A* algorithm to plan the next best path, the state recorded in the bulletin board, through the suboptimal path can be marked with some of the path vector $A_1$, $A_2$, $A_3$, $A_4$, $A_5$, $A_6$, $A_7$ the two endpoints of these vectors as the feasible path of the coordinate point, as shown in Fig. 2 $a_1$, $a_2$, $a_3$ etc. [10], the latter part of the algorithm is to optimize the adjustment of these coordinate points.

The available coordinate points obtained in the previous step can be arranged and combined to form m feasible paths, for example:$\mathrm{}{a}_1{a}_3{a}_4{a}_5{a}_{7\mathrm{}}$, $a_1{a}_2{a}_3{a}_4{a}_6{a}_7$, etc. Each path represents an artificial fish. These feasible paths make up the size of the artificial fish population m, setting the congestion factor of the artificial fish population $\delta$; the visual field of the artificial fish “visual”; the maximum number of iterations Artificial fish “Iterate number” Maximum number of attempts to move each iteration “try number”; artificial fish Mobile step

Each artificial fish chooses the best behavior from improved foraging behavior, clustering behavior and rear-end behavior respectively.

The artificial fish, once performed, compares the status of the newly acquired condition with that of the record in the bulletin board, and replaces the status in the bulletin board if the condition is better than that in the bulletin board;

Determine whether the current number of iterations has reached the maximum number of iterations “Iterate number”, if yes, output the results in the bulletin board, otherwise return to the fourth step to continue.

Fig. 1Curve of attenuation function

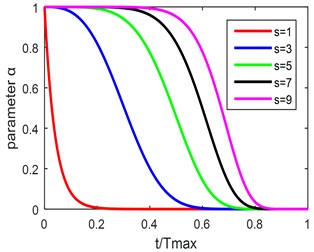
Fig. 2Available vectors and coordinate points schematic

3. Comparison and analysis of experimental results

In this paper, artificial fish swarm algorithm (AFSA), improved artificial fish school algorithm (IAFSA) [11] and hybrid improved artificial fish swarm algorithm (HIAFSA) are simulated in two grids with different obstacles. The size of the grid map is 40×40. The point S in the grid map indicates the starting position of the robot, the point T represents the target position of the path planning, and the gray area indicates the obstacle area.

Fig. 3Complex environment grid map 1 and simple environment grid map 2

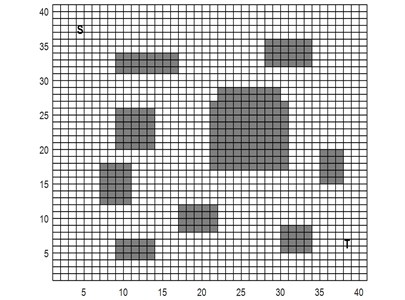
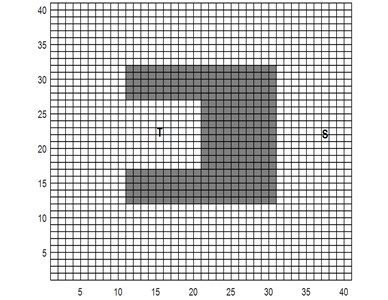
As shown in Fig. 3, the grid map simulation environment more complex map, which is characterized by a wide range of obstacles, uneven distribution and irregular size, the robot need to avoid all the obstacles and the optimal path to plan to reach the end. Fig. 4 shows the raster map simulation environment is a simple map, which is characterized by the situation is relatively simple obstacles, the robot needs to go through the corner of 180° reach the end.

Fig. 4 shows the simulation results of the three algorithms in Map 1 and Map 2. The black solid line indicates the path of the HIAFSA plan, the path of the IAFSA and the AFSA plan is indicated by two dotted lines, and the red mark points indicate the available coordinate points generated by the A* algorithm. As can be seen from Fig. 4(b), the optimal path length generated by the three algorithms of map 2 is very close, and the advantage of HIAFSA is not obvious. This is due to the single obstacle in map 2 and the path length of the IAFSA plan is close to the optimal path length, there is not much room for improvement, but for the complex environment of Map 1, the path generated by HIAFSA is significantly shorter. HIAFSA effectively avoids the algorithm getting into local optima, which leads to better path selection in complex environment. The experiment was repeated 50 times, the experimental results in Table 1 statistics. Max and Min in Table 1 represent the maximum and minimum values of the results obtained in 50 experiments, respectively, and Best represents the ideal optimal value. The average time is the average of the 50 repetition tests. The analysis results show that compared with the other two the results of HIAFSA algorithm show that the HIAFSA algorithm has a smaller average path result and is closer to the theoretical optimal value. Meanwhile, the variance of the HIAFSA algorithm is smaller than the other two algorithms. The experimental results show that the HIAFSA algorithm has higher convergence accuracy, more stable, not volatile, the result is more accurate.

Fig. 4Under different maps of three algorithms path planning simulation

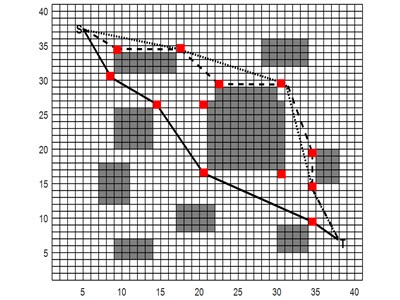
a)

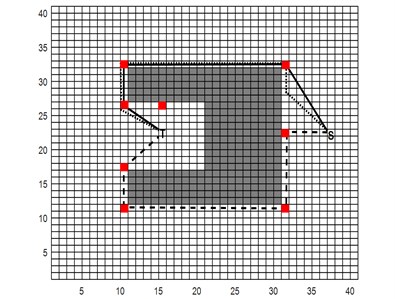
b)

Fig. 5Under different maps three algorithms path planning iteration

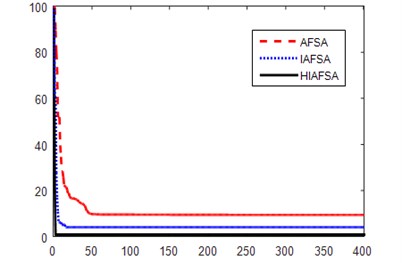
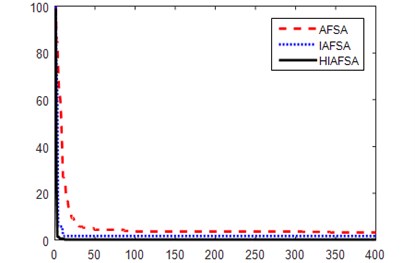
Fig. 5 shows the iteration curves of the three algorithms running once on map 1 and map 2, where the ordinate represents the difference between the optimal path generated by the algorithm and the ideal optimal path, the abscissa represents the number of experimental iterations, The results show that the convergence value of HIAFSA algorithm is closer to the ideal optimal value, and it has a faster convergence rate and reaches the global optimum faster.

In summary, the HIAFSA algorithm has the advantages of fast convergence and high convergence precision and has good global optimization and local optimization capabilities. The HIAFSA algorithm has strong applicability and can obtain ideal results for more complicated problems.

4. Conclusions

In this paper, a hybrid improved artificial fish swarm algorithm is proposed. The A* algorithm and the improved artificial fish swarm algorithm are integrated. the former is used to plan a suboptimal path, and the latter is used to optimize the optimal path so as to obtain the optimal path result, the control parameters of the dynamic adjustment algorithm of attenuation function are introduced, meanwhile the fish population based on nonlinear weighting adaptive behavior is constructed to enhance the global search ability and local search ability of the algorithm in optimization process, and the optimization accuracy of the algorithm is improved; Accuracy and superiority in path planning. the simulation results show that compared with the IAFSA, this algorithm has better quality, faster convergence and more stable convergence, which shows that this algorithm is an effective and improved algorithm.