Study on separation characteristics of two-phase flow in double helical separator

2.1. Calculation model

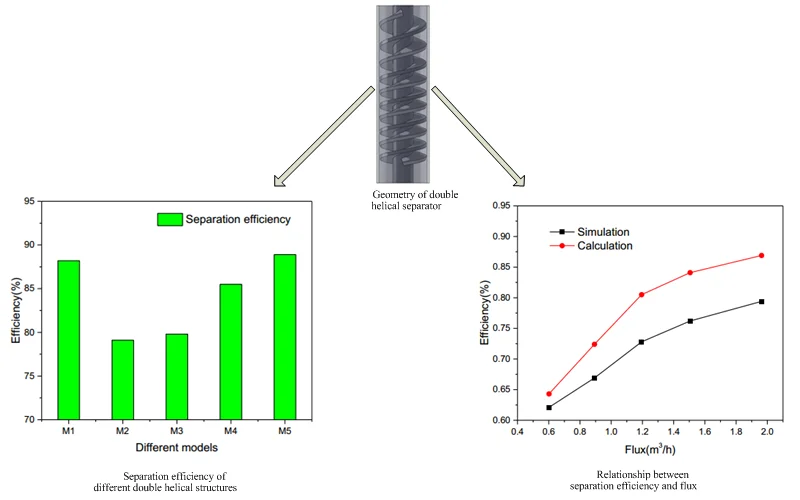
Considering the characteristics of underground environment, the calculated model is simplified and the geometric model of double helical separator with variable pitch is established, as shown in Fig. 1. The outer diameter of helical separator pipe is 100 mm, the even difference of pitch is 10 mm and 15 mm, respectively. Total length is 530 mm and blade thickness is 10 mm-20 mm. For the convenience of calculation and the saving of calculation time and space, the computational fluid must be assumed and simplified. Assuming that the gas-liquid two-phase fluid is incompressible, and the flow is steady turbulent flow. When the fluid is static, the total pressure is static pressure. If the flow entering the separator comes from infinite distance, the inlet velocity is uniformly distributed. Ignoring the friction of pipe wall, the gas-liquid two-phase flow has no heat exchange with the outside environment and its temperature remains unchanged. The mesh generation of separator has great influence on the accuracy of calculation results. The principle of generating mesh is that the regions which are important to the study should be encrypted. In other areas, the distance between nodes can be enlarged appropriately, so that the calculation efficiency can be improved under the premise of ensuring the reliability of calculation. Fig. 2 shows the model grid partitioning method used in numerical calculation in this study. The working medium is water and air at normal temperature. The density of water is 1000 kg/m³ and the density of air is 1.37 kg/m³.

Fig. 1Geometry of double helical separator

Fig. 2Mesh division of geometry model for double helical separator

2.2. Calculation model and boundary condition

In this study, the fluid in the helical separator is regarded as incompressible fluid. RNG $k$-$\epsilon$ model is a turbulence model established by Yakhot and Orzag [5] to correct the standard $k$-$\epsilon$ model. An additional item is added to the $\epsilon$ equation of the RNG $k$-$\epsilon$ model, increasing the accuracy of the fast flow calculation. In the RNG $k$-$\epsilon$ model, we consider the effect of vortex on turbulence, which is the opposite sex of turbulence, increasing the ability to predict rotational flow. At the same time, the coefficient in RNG $k$-$\epsilon$ model is calculated by theoretical formula rather than experience, so it is more adaptable. The equations of the turbulent kinetic energy and the dissipation rate of the turbulent kinetic energy are shown respectively:

where $G_k$ is the generating term of turbulent kinetic energy, model constant $C_{\mu }=$ 0.0845, ${\alpha }_k={\alpha }_{\epsilon }=$ 1.39, $C_{1\epsilon }=$ 1.42, $C_{2\epsilon }=$ 1.68, ${\eta }_0=$ 4.377, $\beta =$ 0.012.

The correlation between turbulent kinetic energy $k$ and turbulent kinetic energy dissipation rate $\epsilon$is still as follows:

It can be seen that the RNG $k$-$\epsilon$ activated model can be used for low Reynolds number flow. In the dissipation rate equation of turbulent kinetic energy, the time average strain rate term reflecting the mainstream is added, reflecting the influence of average strain rate on the dissipation term. Therefore, the RNG $k$-$\epsilon$ model can better handle the flow with high strain rate and large bend of streamline. In view of that the fluid in the helical separator is accompanied by the interaction between turbulence and helical flow, resulting in flow curve and local reflux, the RNG $k$-$\epsilon$ model is adopted in this study to simulate the fluid in the double helical separator.

3.1. The influence of geometric parameters on separation efficiency

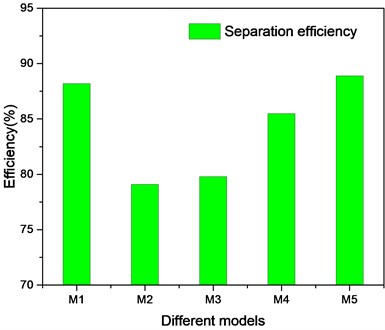
The helical number and pitch of the double helical gas-liquid separator with variable pitch are changed and the influence of structure parameters on the separation efficiency is studied by the method of simulation. Table 1 is double helical gas-liquid separator with variable pitch accompanied five different structure parameters. As shown in Fig. 3, the double helical separator with a flow rate of 1.982 m³/h has the highest separation efficiency when the helical number and gas-liquid ratio are constant. When the flow rate and the gas-liquid ratio are constant, the separation performance of the double helical separator with 10 mm even difference pitch is the best. The greater the gas-liquid ratio and the better the separation efficiency, when flow rate and pitch are constant.

Fig. 3Separation efficiency of different double helical structures

3.2. Separation efficiency at different flow rates

The model based on the mass and momentum balance equations was developed by Alhanati (1993) [6], which was used to predict the natural separation efficiency of two-phase flow. The expression of separation efficiency was expressed as:

where $v_{sl}$ is the superficial velocity of the liquid phase, $\sigma$ is the surface tension, $n$ refers to the flow regime.

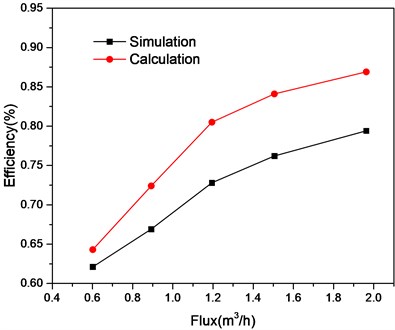
The separation efficiency under different flow rates with the same liquid content rate (the liquid holdup is 80 %) is shown in Table 2. It can be seen from Table 2 that the separation efficiency of double helical separator with variable pitch increases with the increase of flow rate. At the same flow, the numerical simulation data and theoretical calculation results of the separation efficiency of helical separator are similar and the maximum relative error is about 9.5 %. Both theoretical calculation and numerical simulation show that the cyclone intensity of the flow field inside the separator will also increase with the flow rate increases and the inlet velocity increases, which is conducive to the separation of gas-liquid two phases, as shown in Fig. 4.

Fig. 4Relationship between separation efficiency and flux

It can be found that the centrifugal motion of heavy liquid in helical separator and the centripetal motion of light component gas are the fundamental reasons for gas-liquid separation. The strong shear action in the shear layer near the solid wall makes bubbles bound in the liquid drop escape. In the separator, the pressure drops as the potential energy and kinetic energy of the mixed media increase, causing some small bubbles to expand, thus obtaining separated centripetal force, which is an important auxiliary factor for gas-liquid separation.