Abstract
Based on the numerical analysis model of abrasive flow polishing, the effects of fluid turbulent kinetic energy, turbulent intensity and turbulent viscosity on the quality of polishing on polishing quality are studied and analyzed by taking variable diameter pipe as an example. The results of numerical simulation show that the polishing quality becomes better with the decrease of aperture. Therefore, the optimal processing parameters can be simulated according to the specific size of the workpiece, which can provide technical support for the production.
1. Introduction
The rapid development of engineering technology, variable diameter pipe parts are widely used in aerospace, automobile, mechanical processing and other industrial production [1, 2]. However, due to its special structure, the traditional methods of polishing are difficult to polish their inner surface effectively [3, 4]. Abrasive flow polishing technology uses semi-solid abrasive to make the abrasive move to and for on the surface of the machined parts under certain pressure. It can polish all kinds of cavity, cross aperture and edge of the parts [5, 6]. The technology can be used to polish the inner surface of variable diameter parts, improve their surface quality, and make them meet the technical requirements [7, 8]. Therefore, the study of abrasive flow polishing technology has extremely important engineering application value.
2. Geometric model
2.1. Creation of physical model
The variable diameter pipe studied is a coaxial rotating body and its two-dimensional model is shown in Fig. 1.
The variable diameter pipe is divided into four region for the sake of facilitating the analysis of the numerical variation trend of it. The first-order center line, the second-order center line, the third-order center line and the fourth-order center line are located at the transverse center of each region respectively. The center line of workpiece rotating is defined as the origin of the center line of each region and above the center line is positive and below is negative. The abrasive inlet is defined as the origin of the center line of workpiece rotating. Fig. 2 shows the division area of the flow passage of the variable diameter pipe.
Fig. 1The two-dimensional model of the variable diameter pipe
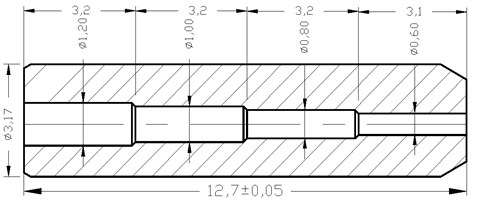
Fig. 2The division area of flow passage

2.2. Meshing of model
The structure of variable diameter pipe is meshed by unstructured hexahedral. After meshing, 441106 nodes are formed in the variable diameter pipe as shown in Fig. 3.
Fig. 3The meshing of model

3. Parameter setting of the model
According to structure characteristics of the variable diameter pipe and the size of the abrasive particle, the length of time step is 2E-7 s and the command of Track Collision is opened. The total time of numerical simulation is 1s. In the simulation process, the Eulerian-Lagrangian method is selected to couple and Sample Points is set to 10. The wall is regard as the solid wall without slip because two ends of the workpiece are fixed by clamps.
4. Analysis of simulation results
Numerical analysis was conducted on the fluid turbulent kinetic energy at the inlet velocity of 45 m/s, abrasive concentration of 10 % and the abrasive particle size is 800 mesh (18 micron).
The variation curves of fluid turbulent kinetic energy in the center lines of different regions were obtained by processing the data as shown in Fig. 4.
From Fig. 4(a) to Fig. 4(d), it can be seen that the turbulent kinetic energy near the wall of the four regions is the largest and the center is small. As shown in Fig. 4(e), the turbulence kinetic energy is the largest at the beginning of each stage, and then gradually decreases. That’s because the abrasive particles collide with the workpiece randomly, consuming part of the energy. Under the same conditions, the turbulent kinetic energy is inversely proportional to the size of the aperture.
The variation curves of fluid turbulence intensity in the center lines of different regions were obtained by processing the data as shown in Fig. 5.
From Fig. 5(a) to Fig. 5(d), the turbulence intensity increases with the decrease of aperture. With the increase of turbulence intensity, the flow of abrasive becomes stronger, the collision between abrasive particles and the wall surface becomes more violent, and the material removal amount becomes larger. Therefore, the increase of turbulence intensity is beneficial to the polishing. As shown in Fig. 5(e), The variation trend of turbulence intensity curve is basically the same as that of turbulence kinetic energy.
Fig. 4Fluid turbulent kinetic energy curve at the center line of different regions
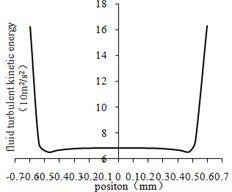
a) The first-order center line
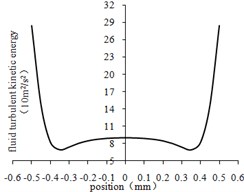
b) The second-order center line
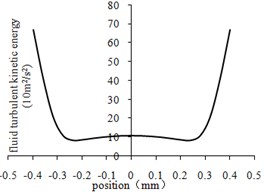
c) The third-order center line
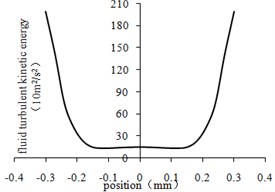
d) The fourth-order center line
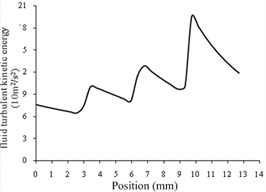
e) The center line of workpiece rotating
Fig. 5Fluid turbulent intensity curve at the center line of different regions
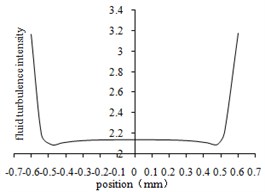
a) The first-order center line
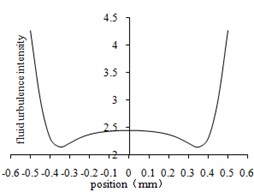
b) The second-order center line
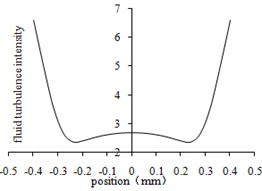
c) The third-order center line
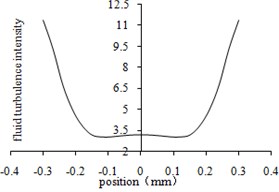
d) The fourth-order center line
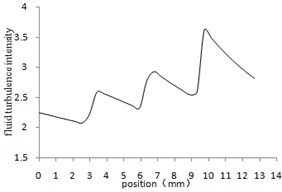
e) The center line of workpiece rotating
The variation curves of fluid turbulence viscosity in the center lines of different regions were obtained by processing the data as shown in Fig. 6.
From Fig. 6(a) to Fig. 6(d), The curve of turbulent viscosity is convex parabola symmetric with the center line of workpiece rotating. The turbulent viscosity reaches its minimum near the wall. As shown in Fig. 6(e), the turbulent viscosity is proportional to the size of the aperture. With the decrease of turbulence viscosity, the flow of abrasive becomes stronger, the collision between abrasive particles and the wall surface becomes more violent, and the material removal amount becomes larger.
Fig. 6Fluid turbulent viscosity curve at the center line of different regions
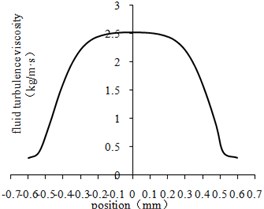
a) The first-order center line
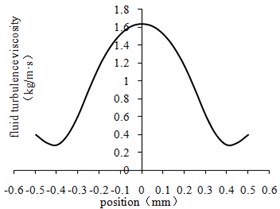
b) The second-order center line
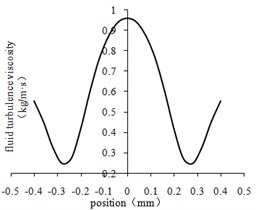
c) The third-order center line
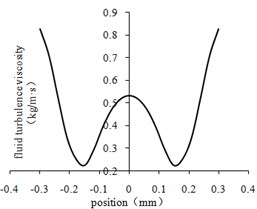
d) The fourth-order center line
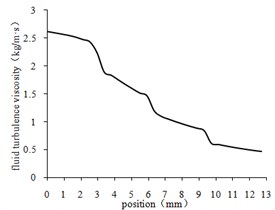
e) The center line of workpiece rotating
To sum up, the polishing quality of the fourth-order region is the best and the first-order region is the worst.
5. Conclusions
In this paper, the degree of material removal on the inner surface of the variable diameter pipe is discussed. The effects of fluid turbulent kinetic energy, turbulent intensity and turbulent viscosity on the quality of polishing was analyzed by numerical simulation. The results of numerical simulation show that these physical quantities are different in the different region of the variable diameter pipe. Under the same process parameters, the polishing quality is inversely proportional to the size of the aperture. Therefore, according to the actual situation, the optimal physical quantity of coupling field through simulation can be obtained, which can provide technical support for the production.
References
-
Deng Yan-Hua, Deng Long-Long, Tu Qun-Lan, et al. Numerical simulation of high-pressure jet tube with abnormal shape and variable diameter. South-to-North Water Transfers and Water Science and Technology, Vol. 12, Issue 3, 2014, p. 108-111+126.
-
Li Jun-Chu, Zhan Li-Na, Xiong Hong-Shen Finite element simulation of shaped tube hydroforming. Hot Working Technology, Vol. 39, Issue 7, 2010, p. 98-100+103.
-
Santhosh Kumar Sa, Somashekhar Hiremathb S. A review on abrasive flow machining (AFM). Procedia Technology, Vol. 25, 2016, p. 1297-1304.
-
Uhlmann E., Schmiedel C., Wendler J. CFD simulation of the abrasive flow machining process. 15th CIRP Conference on Modeling of Machining Operations, Vol. 31, 2015, p. 209-214.
-
Ding Jin-Fu, Liu Run-Zhi, Zhang Ke-Hua, et al. Micro cutting mechanism of abrasive flow precision maching. Optics and Precision Engineering, Vol. 22, Issue 12, 2014, p. 3324-3331.
-
Li Jun-Ye, Hu Jing-Lei, Meng Wen-Qing, et al. Numerical simulation analysis of four-step variable-diameter pipe by solid-liquid two-phase grinding. Vibroengineering Procedia, Vol. 15, 2017, p. 119-123.
-
Uhlmann E., Schmiedel C., Wendler J. CFD simulation of the abrasive flow machining process. Procedia CIRP, Vol. 31, 2015, p. 209-214.
-
Kartal F., Gokkaya H. Effect of abrasive water jet turning process parameters on surface roughness and material removal rate of AISI 1050 steel. Materialprufung, Vol. 57, Issue 9, 2015, p. 773-782.
About this article
The authors would like to thank the National Natural Science Foundation of China No. NSFC51206011, Jilin Province Science and Technology Development Program of Jilin Province No. 20170204064GX, Project of Education Department of Jilin Province No. JJKH20190541KJ, Changchun Science and Technology Program of Changchun City No. 18DY017.
