Modeling of wave processes when the heterogeneous flow is moving in a low-frequency magnetic peristaltic pump of pulsating type

1. Introduction

The modern market offers various designs of pumping equipment capable of pumping heterogeneous mixtures with a high content of solid particles – with a mass concentration up to 80 %. The main types of volumetric pumps in these conditions are piston and peristaltic pumps. In recent years, peristaltic pumps have become more popular for dispensing transported slurry [1]. For example, an innovative approach to transportation to remote and hard-to-reach areas of mine workings of pasty and viscous mixtures during filling operations is the use of low-frequency magnetic peristaltic pumps of the pulsating type (Fig. 1). In this equipment, the mixture moves under the influence of a local undulating deformation of the working channel, made of a magnetoactive elastomer.

Fig. 1General view of a low-frequency magnetic peristaltic pump of the pulsation type

Unlike conventional elastomers, magnetoactive elastomers do not require the use of additional moving parts in the design of the pump working channel [2]. Studies using canal samples from a magnetoactive elastomer of various geometries have shown that in order to increase the efficiency of such a pump, its working channel should have a non-circular cross section. This shortens the distance between the inductors of the running magnetic field generator and contributes to improving the pump performance with a constant channel cross-section area [3]. The uneven distribution of electromagnetic forces over the cross-sectional area of a non-circular channel determines the occurrence of a transverse edge effect, contributing to a decrease in the intensity of transverse channel deformation. To minimize this effect, the inner surface of the channel is made with screw guides. In the process of operation of the magnetic peristaltic pump, the particles of the transported substance perform a sequential process of displacements along a helical line along the flow axis. Low-frequency pulsation compression of the working channel allows pumping the mixture in a single laminar flow at a relatively low shear stress. The shape of the inner surface of the working channel with screw guides ensures longitudinal movement of the slurry stream, simultaneously with its mixing, which prevents stratification of the mixture [4, 5]. Thus, the working channel additionally performs the functions of a quastatic mixer.

2. Materials and methods

Extended studies of hydromechanical processes occurring in the working channel of a magnetic peristaltic pump can be performed by conducting a computational experiment or with the help of a carefully designed physical experiment [6-12]. However, phenomena of practical interest accompanying the process of moving a heterogeneous flow through a channel of variable cross section are characterized by multidimensionality, nonstationarity, and the presence of boundary layers, which makes the implementation of comprehensive physical modeling very difficult.

Simulation modeling of the flow movement according to the twisted quasistatic mixer scheme, performed in the COMSOL Multiphysics software environment, makes it possible to evaluate the mixing efficiency by calculating the trajectories and velocities of suspended particles through the working channel, and also to estimate the pressure loss to overcome the hydraulic resistance of the flow (Fig. 2).

Fig. 2Spatial changes in the kinematic viscosity of the flow in the working channel: arrows indicate the direction of velocity

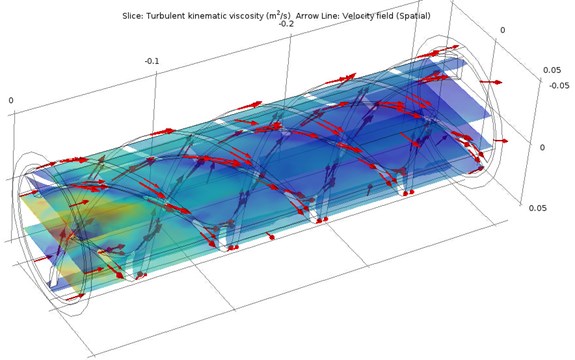
The model explores the mixing of solid particles dissolved in a liquid at a temperature of 20 °C. The flow channel is represented by a channel with three screw guides of variable rotation located on the inner surface. The channel radius is 3 mm, the channel length is 42 mm, the length of each of the screw sections is 9 mm.

The flow at the channel inlet is laminar and moves at a constant average speed of 0.01 m/s. At the outlet of the channel in the model pressure is absent. Laminar flow is described by the equation:

when the flow is obstructed, along with frontal resistance, there are components of viscous forces that are orthogonal to the velocity vector of the body relative to the fluid, which corresponds to the lifting force according to N. Е. Zhukovsky. If macroscopic pulsations form during the flow of the flow in it, this leads to mixing on a macroscopic scale and a change in the values of viscous forces, in particular the drag forces with which the flow acts on the streamlined auger and the wall of the channel.

Particle trajectories are calculated using the Newtonian fluid model using the Stokes law of restraint [13]:

where $v$ – particle velocity, ${\tau }_p$ – particle velocity response time:

where ${\rho }_p$ – fluid density, $d_p^{}$ – particle diameter.

3. Modeling

Modeling the flow of a heterogeneous flow allows you to visualize the distribution of the solid phase and to assess the effectiveness of mixing. The Poincaréplot module was used to study the distribution of the particles of a mixture over the channel cross section and to analyze the mixing efficiency. The work of the module is based on the principle of the follow-up mapping used in the theory of dynamic systems, that is, the projection of a certain site in the phase space onto itself or another, similar to it, along the trajectories of the system.

On the Poincaréplot module, different colors were assigned to particles in their original location: particles with the initial position $x<$ 0 were marked red, and particles with the initial position $x>$ 0 were marked blue (Fig. 3) – this picture was taken as the first Poincare map.

As the particles start to get involved in the flow, their vectors begin to change their directions, and the point of intersection of the trajectory with the next transversal is marked with the corresponding color.

Fig. 3Transversals of particle trajectories in the Poincaré map

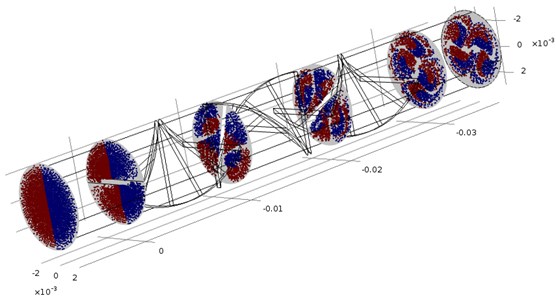
The iteration of the map from the last transversal illustrates the connection between vector fields and particle trajectories. As can be seen from the leftmost transversal in Fig. 3, by the end of the channel the particles are not fully mixed and there are significant pockets where only red and blue particles are concentrated. The distribution density of particles is normalized in accordance with the magnitude of the flow rate at the entrance. This means that more particles are determined at the entrance to the channel, where the magnitude of the velocity is the highest and smaller particles, where the magnitude of the velocity is small. Since particles have mass, they do not all reach the last transversal at the channel exit. In this configuration, the working channel of the magnetic peristaltic pump of 3000 particles at the channel entrance for about 20 % of the particles of the Poincare display was not determined, that is, the relative transfer efficiency of the solid slurry was about 80 %, and some of the particles settled on the surface of the working channel. Also noteworthy is the fact that as it moves along the channel, the flow is structured and, due to the internal geometry, the particles rush to the center of the channel, thus avoiding rapid wear of the working surface.

Based on the known material properties of the working channel and the parameters of the transported substance, the model allows estimating the expanding forces on the tube walls, as well as estimating the necessary force for moving a portion of the substance.

4. Discussion

Experimental studies on installations of pipeline transport of this type allow us to establish the nature of the movement of the slurry when exposed to the working channel of a running magnetic field. Studies were conducted with the same length and diameter of the tube on samples of substances with different viscosity. The graph of the dependence of the speed of movement of the material on the current strength in the coils of the winding of the generator of a traveling magnetic field is shown in Fig. 4.

Fig. 4The effect of current in the coils of the winding on the speed of movement of a local deformation wave in a traveling magnetic field

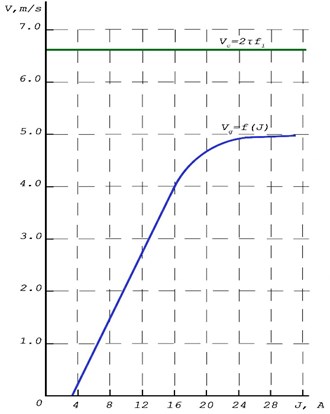
Observations have shown that the speed of movement of a wave of local deformation when moving various materials is fairly stable and slightly depends on the viscosity of the substance.

5. Conclusions

The developed model of a heterogeneous flow allows you to describe in detail the state of the slurry at all points of the volume under consideration at specific points in time, and also take into account the complicating factor of nonstationarity of the three-dimensional flow process in the channel of varying geometry and variability of flow properties. The model allows you to set the laws of change of parameters at the boundaries of the calculated region in terms of the wave variation of the internal cross section of the working channel under the influence of the energy of a running magnetic field.