Abstract
The dynamic response of machine foundations was one of the first problems studied in soil dynamics with results going back to the 1930s. A number of approximations and graphical results were proposed in the 60s. In this paper we present a series of approximate expressions for the natural frequencies and effective damping of rigid masses on the surface of an elastic half space subjected to both vertical and coupled horizontal-rocking harmonic excitations. The formulas are obtained using the approximate expressions for the dynamic stiffness of circular foundations suggested by Veletsos et al [1, 2] for two different values of Poisson’s ratio of the soil. For the vertical case the expressions are only a function of the mass ratio (ratio of the mass of the foundation to an effective mass of soil) and of Poisson’s ratio. For the horizontal-rocking case they depend also on the ratio of the height of the foundation to its equivalent radius (a slenderness ratio).
Highlights
- Proposed expressions to improve the estimates of the natural frequencies by iterating with values of the rotational stiffness computed at each one of the obtained frequencies.
- For the horizontal/rocking case, the variation of natural frequencies and effective damping are function of the mass ratio whereas the Poisson ration has a negligible effect.
- By fitting the exact solutions, expressions to evaluate the dimensionless frequencies and damping ratios as a function of the aspect ratio are proposed.
1. Introduction
The design of foundations to support heavy machinery that could induce vibrations was already recognized as an important practical problem in the 1930s giving rise to the field of Soil Dynamics. In the thirties Reissner [3, 4] derived the first analytical solution for the vertical displacements on the surface of a linear elastic, homogeneous, and isotropic half space subjected to a harmonic normal stress uniformly distributed over a circular area. The solution for the vertical case was followed immediately by a solution for torsional vibrations. Work along these lines was continued in the following years by Reissner and Sagoci [5] and by Shekhter [6], who used the average of the displacements at the center and at the edge of the loaded area to obtain curves of dynamic amplification as a function of a dimensionless frequency and a mass ratio. These curves were widely used.
The fifties saw a significant increase both in the number of researchers engaged in this area and in the number of related publications. The solution of the true mixed boundary value problem, where stresses are specified along the surface of the soil, outside the area of the foundation (stress free surface) while displacements are imposed at the base of a rigid and massless body, was addressed by Borodatchev in 1964 [7] for the vertical case. A rigorous solution for the dynamic stiffness of a rigid and massless circular foundation on the surface of a linear elastic, homogeneous and isotropic half space was presented in graphical and tabular form over an extended range of frequencies by Veletsos and Wei [1] for the coupled horizontal and rocking vibrations, in 1971 an independent solution was published by Luco and Westmann [8] almost at the same time. Additional results for vertical and torsional excitations and for viscoelastic or hysteretic media were obtained by Veletsos and Verbic [2].
At the same time that the analytical formulations were developed, Reissner explored the possibility of reproducing his results with a lumped parameter model consisting of a mass, a spring and a dashpot, but he concluded that their values would have to be functions of frequency, and he could not find simple expressions for them. Whitman and Richart in 1967 [9] used again lumped parameter models with springs, masses and dashpots to provide graphical results for the amplitudes of vibration of a machine foundation as a function of frequency in terms of a mass ratio. In the 70s Veletsos and Wei [1] and Veletsos and Verbic [2] found approximate but accurate expressions for the foundation stiffness terms of a rigid circular mat on the surface of an elastic, homogeneous and isotropic half space as function of the dimensionless frequency and these are still the best simplified formulas available to date. This work presents approximate explicit expressions for the natural frequencies and effective damping in each mode of a rigid mass on the surface of an elastic half space subjected to both vertical and coupled horizontal/rocking harmonic excitations. These formulas are intended for preliminary estimates when designing machine foundations.
2. Formulation
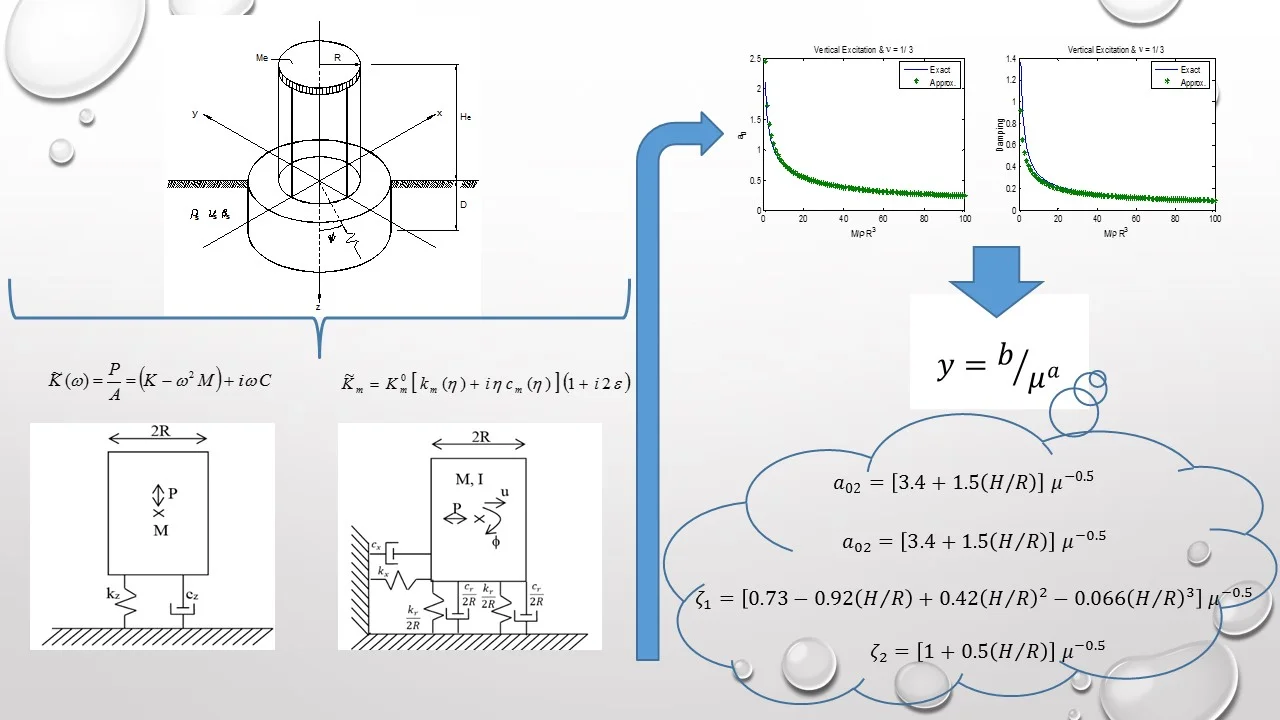
It is considered a rigid cylindrical mass representing a machine foundation resting on the surface of an elastic half space. Calling the total mass, the mass moment of inertia with respect to the center of gravity, the height of this point, the radius, the shear wave velocity of the soil, its shear modulus, its mass density and Poisson’s ratio, one can consider both vertical and coupled horizontal-rocking vibrations. A schematic representation of the mass is shown in Fig. 1.
Fig. 1Rigid mass on elastic halfspace system
2.1. Vertical excitation
For the vertical case the amplitude of the response and the effective damping will depend on the ratio between the mass of the foundation and a soil mass . Using the formulas for the dynamic stiffness (spring stiffness and dashpot) of a circular mat foundation proposed by Veletsos and Verbic [2].
For a :
For a :
where is a dimensionless frequency and is the circular frequency of the excitation.
The natural frequency would then be the value of solution of , and the effective damping at the natural frequency would be:
In terms of the natural frequency in terms of the mass ratio is then given by.
For :
For :
The circular natural frequency is then and the effective damping at the natural frequency is.
For :
For :
For values of the mass ratio larger than 20 one can use approximate formulas.
For :
For :
2.2. Horizontal-rocking vibrations
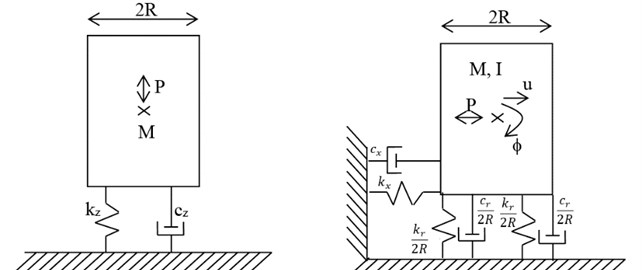
Assuming a unit harmonic horizontal force applied at the center of mass the steady state responses for the horizontal displacement of this point and the rotation of the mass require the solution of the system of equations:
where the components of the displacement vector are (translation) and (rotation) and the components of the load vector are 1 and 0. The stiffness, damping and mass matrices are:
where is the height of the center of mass with respect to the base.
Using the approximate expressions suggested by Veletsos and Wei [1] for a circular mat foundation on the surface of an elastic half space with a Poisson’s ratio of 1/3.
For :
For :
and:
Explicit solutions for this case are more difficult to obtain because of dealing with a two degree of freedom system. The results will depend not only on the mass ratio but also on the aspect ratio . A procedure often used in practice is to obtain the natural frequencies and mode shapes of the 2 degree of freedom system using the static values of the horizontal and rotational stiffness, then compute the values of the dashpots at these frequencies, assemble the damping matrix, and determine the values of damping neglecting the off-diagonal terms of the matrix and assuming that the system has normal modes with values of damping with the diagonal terms of this matrix equal to and , respectively.
One could improve the estimates of the natural frequencies by iterating with values of the rotational stiffness computed at each one of the obtained frequencies and this is the procedure used here. However, the values of the modal damping were still obtained using the above mentioned approximation.
3. Results
The explicit expressions for the natural frequency and damping for the vertical case were already included with the formulation. Fig. 2 compares the results using the exact expressions with those provided by the suggested approximate formulas. The results show that the approximate expressions provide a very good accuracy for values of the mass ratio larger than 10.
For the horizontal/rocking case, the variation of the 2 dimensionless natural frequencies , and the corresponding estimated values of the effective damping at these frequencies as a function of the mass ratio are shown in Figs. 3 and 4 for aspect ratios of 1, 1.5, 2 and 2.5, as well as for Poisson’s ratios of 1/3 and 1/2. These results show that the Poisson ratio has a negligible effect on the solution, although the damping ratio shows larger differences, these still are negligible.
Fig. 2Dimensionless frequencies and damping for the vertical case
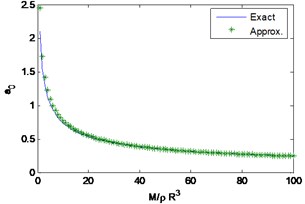
a)1/3
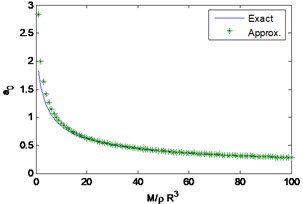
b) 1/2
The dimensionless frequencies and the associated values of damping for the 2 modes can be expressed in the form:
where the coefficients and are functions of the Poisson’s ratio and the slenderness ratio . The exponent is relatively insensitive to the values of the Poisson’s ratio and (except for the lower values of , the second mode and in particular the damping in that mode). It is approximately 0.5 as for the approximate expressions proposed earlier for the vertical case. The factor b is also relatively insensitive to Poisson’s ratio but depends strongly on . It decreases with increasing for the first mode (natural frequency and associated damping) and it increases for the second mode. Fitting the exact solutions, we propose the following expressions to evaluate de dimensionless frequencies and the damping ratios as a function of the aspect ratio and independently of the Poisson’s ratio:
These expressions were obtained fitting the numerical results obtained for values of between 0.5 and 2.5. In the limit as tends to 0 there would be only one natural frequency and the average expressions for a Poisson’s ratio between and would be and . The first is about 10 % higher than the value provided by the suggested formula while the second is almost exactly the same. Figs. 3 and 4 show a comparison of the results obtained with the approximations and the exact solutions. The results for an aspect ratio of 0.5 are not presented for lack of space. These results show that the proposed formulas are quite accurate for less than 2.5.
Fig. 3Exact vs. approximate solutions for a01 and a02
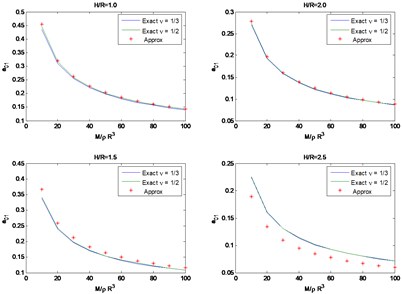
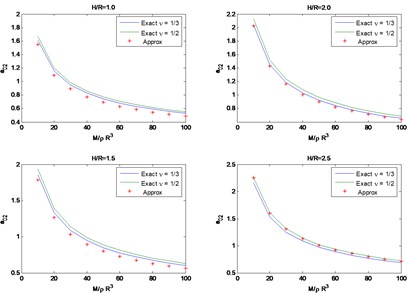
Fig. 4Exact vs. approximate solutions for ζ1 and ζ2
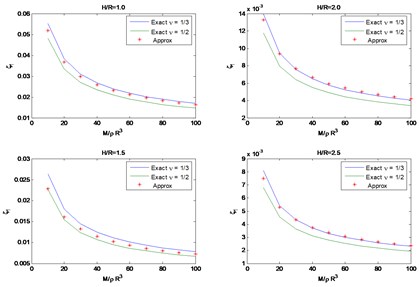
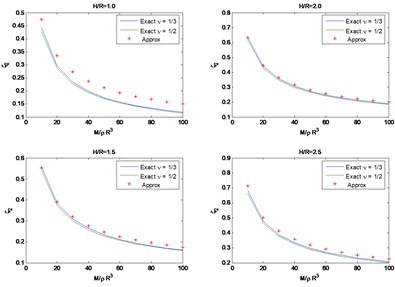
4. Conclusions
A series of approximate expressions have been presented to estimate the natural frequencies and associated damping of rigid masses on the surface of an elastic half space. These expressions provide in general a reasonable accuracy and should be of value for preliminary estimates at the early stages of a design. The results indicate that the dimensionless frequencies are essentially proportional to the radius to the exponent 3/2. This implies that the actual frequencies in rad/sec or Hz would be proportional to the square root of the radius and the square root of the soil modulus as would have been predicted using the static values of the foundation stiffness terms.
References
-
Veletsos A., Wei Y. Lateral and rocking vibration of footings. Journal of the Soil Mechanics and Foundations, Vol. 97, 1971, p. 1227-1248.
-
Veletsos A., Verbic B. Vibration of Viscoelastic Foundations. Report No. 18, Structural Research at Rice, Civil and Environmental Engineering, Rice University, Houston, 1973.
-
Reissner E. Stationare, axialsymmetrische, durch schuttelnde Masse erregte Schwingungen eines homogenen elastichen Halbraumes. Ing. Archive, Vol. 7, 1936, p. 381-396.
-
Reissner E. Freie u. erzwungene Torionsschwingungen des elastischen Halbraumes. Ing. Archive, Vol. 8, Issue 4, 1937, p. 229-245.
-
Reissner E., Sagoci H. F. Forced Torsional Oscillations of an elastic halfspace. Journal of Applied Physics, Vol. 15, Issue 9, 1944, p. 652-662.
-
Shekhter Ya O. Consideration of inertial properties of soil in the computation of vertical forced vibrations of massive foundations. Vibratsii Osynovaniy I Fundamentov, Moscow, 1948.
-
Borodatchev N. M. Dynamic contact problem for a rigid body with a flat circular base resting on elastic half-space. Proceedings of the USSR Academy of Sciences, Mekhanika i Mashinostroenie, 1964.
-
Luco J. E., Westmann R. Dynamic response of circular footings. Journal of Engineering Mechanics, Vol. 97, 1971, p. 1381-1395.
-
Whitman R. F., Richart F. E. Design procedures for dynamically loaded foundations. Journal of Soil Mechanics and Foundations, Vol. 93, Issues 6-5569, 1967, p. 169-193.
