Level set medical image segmentation aided by cooperative quantum particle optimization with Lévy flights

Li, Desheng; Deng, Na; Chen, Xu

doi:10.21595/vp.2019.21054

Vibroengineering Procedia

Browse Procedia

Published: 19 October 2019

Check for updates

Level set medical image segmentation aided by cooperative quantum particle optimization with Lévy flights

Desheng Li¹

Na Deng²

Xu Chen³

¹College of Information and Network Engineering, Anhui Science and Technology University, Bengbu, 233000, China

²School of Computer, Hubei University of Technology, Wuhan, 430068, China

³School of Information and Safety Engineering, Zhongnan University of Economics and Law, Wuhan, 430073, China

Corresponding Author:

Desheng Li

Cite the article Download PDF

Downloads 1365

CrossRef Citations 4

Abstract

Image segmentation plays an important part of image processing, and is also the premise and basis of image analysis and image understanding and recognition. Among the level set based methods, the original Local Binary Fitting (LBF) algorithm is a successful deterministic algorithm that suffers from sensitization to size of the local minimum, image contours, shapes, and initial positions. Among them, Level Set method promotes the two-dimensional problem to the three-dimensional one and then solves it using implicit method to express closed curve of plane. In this article, a novel Level Set model aided by PSO was proposed to solve automated medical image segmentation. The experimental result of segmentations on the benchmark shows that our proposed method is effective to both simple and complex medical images.

Level set medical image segmentation aided by cooperative quantum particle optimization with Lévy flights

Highlights

The Gaussian filtering is used to smooth the level set rather than the penalty term
As the import of the Lévy Flights, the noise disturbance is greatly reduced.
The proposed algorithm could reach high SPM, i.e., achieve desired initialization insensitive segmentation performance for both simple and complex medical images.

1. Introduction

Image segmentation plays an important part of image processing, and is also the premise and basis of image analysis and image understanding and recognition. As the split structure is surrounded by other ones with similar structural strength, many existing classic segmentation techniques [1] (multi-threshold technology, regional growth and morphological filtering, etc.) just get general effect of segmentation.

Among them, Level Set method [2] promotes the development of the initiative geometric active contour model greatly as the mainstream direction of the methods based on energy functional theory. However, there are also some problems and/or shortcomings: for example, it requires the whole updates for the level set function values of all points of the entire image in the topology changes of adaptive evolution curve, which consume a lot of calculation; numerical convolution and partial differential equations also spend abundant computing time. Therefore, the overall efficiency of level set method is not high and difficult to be applied into practical applications. Especially, some level set methods, such as LBF method [3, 4], are sensitive to size of the local image contours, shapes, and initial positions. In addition, the most current level set models are usually non-convex energy functionals, whose solutions are the local minima rather than global ones. So it is difficult to achieve the desired segmentation results, but also affects the effectiveness of the algorithm.

In recent years, with the search ability, fast convergence speed and other characteristics, particle swarm optimization has been becoming the in-fact standard optimization algorithm. One important stream of research on particle swarm itself includes multi-population co-evolution, space partition and contraction. One most common and effective type is the cooperative particle swarm algorithm (Cooperarive PSO, CPSO) proposed by Fans Van den Bergh [5], which starts at the partition on the dimension of the particles of standard particle swarm optimization, and lets the multiple groups optimize respectively, and then calculates the fitness totally and updates by rules. In our previous work [6, 7], we developed an algorithm combining the Lévy flights and dynamic areas and then applied it in the realistic problems.

The current study shows that the particle swarm optimization has not been deeply embedded in the level set method as an organic integrity. It is possible to use PSO to replace some unnecessary convolution operations and take the advantages of strong searching capability and fast convergence speed. Moreover, most research also not combine the regularization model into it and promote the global performance. On the other side, the image segmentation algorithm based on level set is essentially an optimization problem, which minimizing the energy functional. Hence, the variational level set model of energy functional minimization problem could be formalized into meta-heuristic optimization problem, and by using the particle swarm optimization method and level set competitive image segmentation method. In this article, we embed the particle swarm optimization into the LBF model and algorithm to implement the inner optimization operation and test it on the medical image segmentation.

2. Review of LBF algorithm

2.1. The classic LBF algorithm

In LBF, the complete curve evolution equation is as follows:

1

\frac{\partial ϕ}{\partial t} = μ (∆ ϕ - d i v (\frac{\nabla ϕ}{|\nabla ϕ|})) + ν δ_{ϵ} (ϕ) d i v (\frac{\nabla ϕ}{|\nabla ϕ|}) - δ_{ϵ} (ϕ) (λ_{1} e_{1} - λ_{2} e_{2}),

where $e_{1} (∙)$ and $e_{2} (∙)$ are defined as follows:

2

e_{1} (x) = \int_{Ω}^{} K_{σ} (x - y) {|I (y) - f_{1} (x)|}^{2} d y, e_{2} (x) = \int_{Ω}^{} K_{σ} (x - y) {|I (y) - f_{2} (x)|}^{2} d y .

Heaviside function $H$ is approximated by a smooth function $H_{ϵ}$ which is defined by the following formula:

3

H_{ϵ} (x) = \frac{1}{2} [1 + \frac{2}{π} a r c t a n (\frac{x}{ϵ})] .

The fitting functions $f_{1} (x)$ and $f_{2} (x)$ will be updated according to the following equations:

4

f_{1} (x) = \frac{K_{σ} (x) * [H_{ϵ} (ϕ) I (x)]}{K_{σ} (x) * H_{ϵ} (ϕ)} {, f}_{2} (x) = \frac{K_{σ} (x) * [1 - H_{ϵ} (ϕ) I (x)]}{K_{σ} (x) * [1 - H_{ϵ} (ϕ)]},

where $ϵ$ is a positive constant which is often set to 1.0 to equal to the fixed space steps $δ (∙)$ is the Dirac function and the corresponding derivative of $H_{ϵ}$ could be the smoothed Dirac function with the below form:

5

δ_{ϵ} (ϕ) = H_{ϵ}^{'} (x) = \frac{d}{d x} H_{ϵ} (x) = \frac{1}{π} \frac{ϵ}{ϵ^{2} + x^{2}} .

The main procedure of classic LBF can be summarized as following Algorithm 1 (Table 1). Firstly, the initial level set function $ϕ^{0}$ is simply defined as a binary function:

6

ϕ^{0} (x) = \{\begin{matrix} - c_{0}, x \in R^{2}, \\ c_{0}, e l s e, \end{matrix}

where $c_{0}$ is a constant and $R^{2}$ is an arbitrarily given subset in the image domain.

Table 1Algorithm 1

Algorithm 1. The pseudo-code of LBF

Initialization:

Read the input image

I : Ω \subset R^{2}

.

Build the initial level set function

ϕ^{0}

.

Initialize the iteration number

n = 0

.

Scale parameter in Gaussian kernel.

Repeat:

Compute Heaviside function according to Eq. (3);

Compute Dirac function according to Eq. (5);

Compute

e_{i}

according to Eq. (2);

Update the value of

f_{1} (x)

and

f_{2} (x)

using Eq. (4);

Update the level set function as

ϕ^{n + 1}

according to Eq. (1);

Until

|ϕ^{n + 1} - ϕ^{n}| < T H

;

Output the segmentation result

{ϕ = ϕ}^{n + 1}

.

3. Our proposed algorithms

3.1. CQPSO-LF algorithm

Based on our previous work in [6, 7], we have presented the proposed CQPSO-LF algorithm in steps in Algorithm 2 (Table 2).

Table 2Algorithm 2

Algorithm 2. The pseudo-code of CQPSO-LF

Initialization: Generate the positions randomly.

Repeat

SubSwarm Evaluation: Evaluate the fitness values of particles in sub-swarms according to the fitness function, and get

C_{d}

,

P_{i d}^{b e s t}

, and

P_{g d}^{b e s t}

.

SubSwarm Disturbance: Obtain the values

P_{g d}^{b e s t'}

,

C_{d}^{'}

, by Lévy flights disturbance.

Overall Evaluation: Elect the compositional global best position

P_{c g d}^{b e s t}

.

Overall Disturbance: Obtain the

P_{c g d}^{b e s t'}

by Lévy flights disturbance.

Update Position: Renovate the positions of particles

P_{i d}^{t + 1}

.

Until iteration > TH.

3.2. CQPSO-LF aided LBF algorithm (LBF-CQPSO-LF)

The original LBF algorithm is a deterministic algorithm that is also sensitive to size of the local image contours, shapes, and initial positions. In light of this shortcoming of the algorithm, we propose a new hybrid model in this article to utilize a population based swarm intelligence algorithm to select the good candidate contours with the global minimum of the fitting energy functional. Meanwhile, the level set method is also used to evolve the candidate contours and also get the cost function. During the iterations, the initial seeds are elected by the CQPSO-LF algorithm to achieve the best performance segmentation of the image. The whole framework of the CQPSO-LF aided LBF Algorithm (LBF-CQPSO-LF) is described in the Algorithm 3 (Table 3).

4. Experimental results and analysis

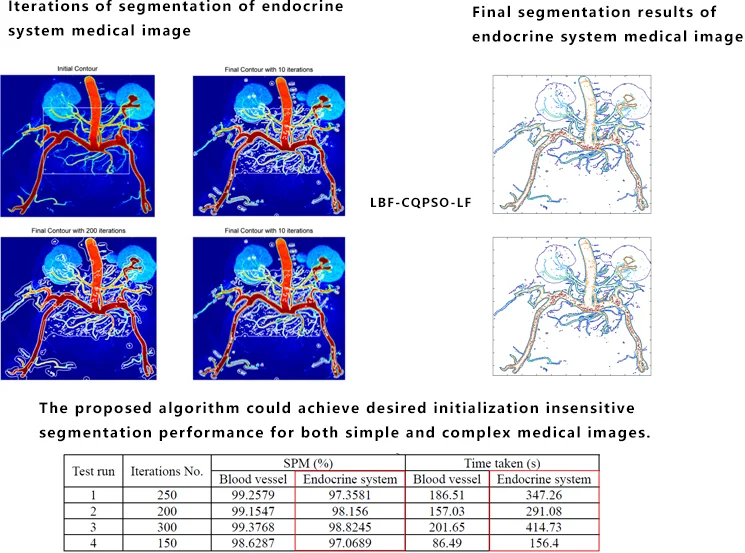
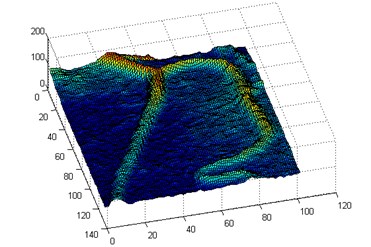
The aim of the experiment is to evaluate the effectiveness of LBF-CQPSO-LF method. At first, we choose one simple blood vessel image to test the validity of the method. The 3D landscape of the blood vessel image is shown in Fig. 1. As shown in Fig. 2, the method could not only segment out the desired objects increasingly, but also is stable to initial contours. Meanwhile, the preprocessing of the image is considered to make the level set regularized as much as possible. To achieve this purpose, we use the Gaussian filtering process to smooth the level set rather than the penalty term proposed by Li et al. [3, 4], which has been verified as a good substitute in literature [10, 11].

Table 3Algorithm 3

Algorithm 3. The pseudo-code of LBF-CQPSO-LF

Initialization:

Read the input image

I : Ω \subset R^{2}

.

Build the initial level set function

ϕ^{0}

.

Initialize the iteration number

n = 0

.

Scale parameter in Gaussian kernel.

While iteration < TH

For

k =

1 to

N

Compute Heaviside function according to Eq. (3);

Compute Dirac function according to Eq. (5);

Compute

e_{i}

according to Eq. (2);

Upate the value of

f_{1} (x)

and

f_{2} (x)

using Eq. (4);

Upate the level set function as

ϕ^{n + 1}

according to Eq. (1);

Until

|ϕ^{n + 1} - ϕ^{n}| < T H

;

Output the segmentation result

{ϕ = ϕ}^{n + 1}

.

End For

For

k =

1 to

N

SubSwarm Evaluation: Evaluate the fitness values

E^{L B F} (C, f_{1}, f_{2})

of particles in sub-swarms according to the fitness function, and get

C_{d}

,

P_{i d}^{b e s t}

, and

P_{g d}^{b e s t}

.

SubSwarm Disturbance: Obtain the values

P_{g d}^{b e s t'}

,

C_{d}^{'}

, by Lévy flights disturbance.

Overall Evaluation: Elect the compositional global best position

P_{c g d}^{b e s t}

.

Overall Disturbance: Obtain the

P_{c g d}^{b e s t'}

by Lévy flights disturbance.

Update Position: Renovate the positions of particles

P_{i d}^{t + 1}

.

End For

End While

Fig. 13D landscape of the blood vessel image

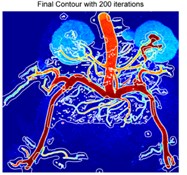
In the sequent experiment, we utilized the LBF-CQPSO-LF in the real application scenario, i.e., an endocrine system medical image. To show the details explicitly, we transformed the image into pseudo-color in the view of Matlab. The initial contour and ones in the iterations are as shown in Fig. 3. The initial rectangular region is fixed in the center of the image, which is not sensitive to the final result any more. Due to the stochastic characteristic of this algorithm, some targets with weak boundaries could be well identified at Fig. 3(b-d).

The final segmentation results of endocrine system medical image after post-processing can be found in Fig. 4(a, b). Totally, the proposed algorithm can avoid the trapping in the local minima when the energy functional evolves. Moreover, as the import of the Lévy Flights, the noise disturbance is greatly reduced. Especially, after removing trivial edges, the refined segmentation can be seen in the Fig. 4(b) with the integrated and clean topological structures, which could be the input of the further analysis.

Fig. 2Iterations of segmentation of blood vessel image

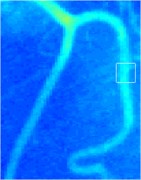
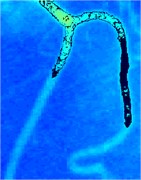
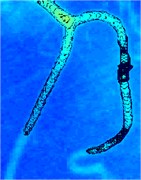
Fig. 3Iterations of segmentation of endocrine system medical image

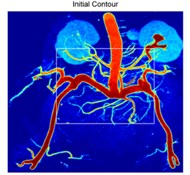
a)

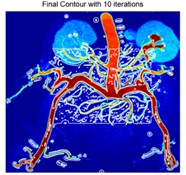
b)

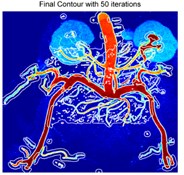
c)

d)

Fig. 4Final segmentation results of endocrine system medical image

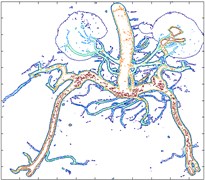
a)

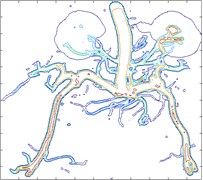
b)

Table 4Performance of LBF-CQPSO-LF

Test run	Iterations No.	SPM (%)		Time taken (s)
Test run	Iterations No.	Blood vessel	Endocrine system	Blood vessel	Endocrine system
1	250	99.2579	97.3581	186.51	347.26
2	200	99.1547	98.156	157.03	291.08
3	300	99.3768	98.8245	201.65	414.73
4	150	98.6287	97.0689	86.49	156.4

To evaluate the performance of proposed algorithm, LBF-CQPSO-LF, we adopted an index called Segmentation Performance Measure (SPM) imported in literature [12] as an benchmark, where the Automatically Segmented Image (ASI) is used to compare with the Manually Segmented Image (MSI) to calculate the similarity by Eq. (7). Table 4 presents the quantitative segmentation performance of blood vessel and endocrine system sample images by SPM and running time. It can be seen that the proposed algorithm could reach high SPM, i.e., achieve desired initialization insensitive segmentation performance for both simple and complex medical images:

7

S P M = \frac{2 * (A S I \cap M S I)}{|A S I| + |M S I|} .

5. Conclusions

In this article, a novel level set model aided by PSO was proposed to solve automated medical image segmentation. In our algorithm, the variational level set model of energy functional minimization problem has been formalized into the meta-heuristic optimization problem. Hence, we embed the particle swarm optimization with Lévy flights into the classic LBF to implement the inner optimization operation in order to accelerate convergence. According to the state of art, our method is novel and unique in this research field of world. The experimental result of segmentations on the benchmark shows that our proposed method is effective to both simple and complex medical images. As our future studies, we will investigate how to expand this method to the three-dimension case and consider multi-phase level sets circumstance. Moreover, as the limitation of slow convergence, we aim to promote the rate of convergence according to some approximate methods. Additionally, we will also explore more effective models to evolution of the level set curves of medical images according to their characteristics.

References

Gonzalez C. R., Woods R. E. Digital Image Processing. Prentice Hall, 2001.

Search CrossRef
Li C., Xu C., Gui C., Fox M. D. Level set evolution without re-initialization: a new variational formulation. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005.

Search CrossRef
Li C., Kao C., Gore J., Ding Z. Implicit active contours driven by local binary fitting energy. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, 2007.

Publisher
Li C., Kao C., Gore J. C., Ding Z. Minimization of region-scalable fitting energy for image segmentation. IEEE Transaction on Image Process, Vol. 17, Issue 10, 2008, p. 1940-1949.

Publisher
Bergh F. V. D. A Cooperative approach to particle swarm optimization. IEEE Transaction on Evolutionary Computation, Vol. 8, Issue 3, 2004, p. 225-239.

Publisher
Li D., He Q., Chen Y. Velocity control of longitudinal vibration ultrasonic motor using improved Elman neural network trained by CQPSO with Lévy flights. Journal of Vibroengineering, Vol. 16, Issue 2, 2014, p. 735-747.

Search CrossRef
Li D. Cooperative quantum-behaved particle swarm optimization with dynamic varying search areas and Lévy flight disturbance. The Scientific World Journal, Vol. 2014, 2014, p. 370691.

Publisher
Coelho L. D. S. Novel Gaussian quantum-behaved particle swarm optimiser applied to electromagnetic design. IET Science, Measurement and Technology, Vol. 1, Issue 5, 2007, p. 290-294.

Publisher
Liu J., Sun J., Xu W. B. Design IIR digital filters using quantum-behaved particle swarm optimization. Advances in Natural Computation, Lecture Notes in Computer Science, Springer, Berlin, Heidelberg, Vol. 4222, 2006, p. 637-640.

Publisher
Zhang K. H., Song H. H., Zhang L. Active contours driven by local image fitting energy. Pattern Recognition, Vol. 4, Issue 43, 2010, p. 1199-1206.

Publisher
Liu S., Peng Y. A local region-based Chan-Vese model for image segmentation. Pattern Recognition, Vol. 45, 2012, p. 2769-2779.

Publisher
Mandal D., Chatterjee A., Maitra M. Robust medical image segmentation using particle swarm optimization aided level set based global fitting energy active contour approach. Engineering Applications of Artificial Intelligence, Vol. 35, Issue 2, 2014, p. 199-214.

Publisher

Cited by

Multilevel Colonoscopy Histopathology Image Segmentation Using Particle Swarm Optimization Techniques

Anusree Kanadath | J. Angel Arul Jothi | Siddhaling Urolagin

(2023)

Chaotic multi verse improved Harris hawks optimization (CMV-IHHO) facilitated multiple level set model with an ideal energy active contour for an effective medical image segmentation

Rangu Srikanth | Kalagadda Bikshalu

(2022)

Nucleus image segmentation method based on GAN and FCN model

Kai Zhang | Yang Shi | Chengquan Hu | Hang Yu

(2022)

Segmentation Technology of Nucleus Image Based on U-Net Network

Jie Fang | QingBiao Zhou | Shuxia Wang | Yi-Zhang Jiang

(2021)

About this article

Received

21 September 2019

Accepted

28 September 2019

Published

19 October 2019

SUBJECTS

Biomechanics and biomedical engineering

DOI

https://doi.org/10.21595/vp.2019.21054

Keywords

level set

segmentation

particle optimization

Lévy flights

active contour

Acknowledgements

This research was supported by Natural Science Foundation of Anhui Province under Grant 1708085MF161, in part by Key Project of Natural Science Research of Universities in Anhui under Grant KJ2015A236, Philosophical and Social Sciences Research Project of Hubei Education Department under Grant 19Q054, and Research Foundation for Advanced Talents of the Hubei University of Technology under Grant BSQD12131.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 10 09

DIC measurement method based on binocular stereo vision for image 3D displacement detection

Xue Dong

Research article

2019 12 31

Tool development for automating the structural integrity assessment of aircrafts’ components

D. G. Stamatelos, V. Kappatos

Research article

2019 08 15

An adaptive stochastic resonance method based on multi-agent cuckoo search algorithm for bearing fault detection

Kuo Chi, Jianshe Kang, Rui Tong, Xinghui Zhang

Research article

2019 06 30

Three-dimensional reconstruction of medical images based on 3D slicer

Xiaolin Zhang, Kexin Zhang, Qiuling Pan, Jincai Chang

D. Li, N. Deng, and X. Chen, “Level set medical image segmentation aided by cooperative quantum particle optimization with Lévy flights,” Vibroengineering PROCEDIA, Vol. 28, pp. 93–98, Oct. 2019, https://doi.org/10.21595/vp.2019.21054

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2019.21054
UR  - https://doi.org/10.21595/vp.2019.21054
TI  - Level set medical image segmentation aided by cooperative quantum particle optimization with Lévy flights
T2  - Vibroengineering PROCEDIA
AU  - Li, Desheng
AU  - Deng, Na
AU  - Chen, Xu
PY  - 2019
DA  - 2019/10/19
PB  - JVE International Ltd.
SP  - 93-98
VL  - 28
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Li_2019,
	doi = {10.21595/vp.2019.21054},
	url = {https://doi.org/10.21595/vp.2019.21054},
	year = 2019,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {28},
	pages = {93--98},
	author = {Desheng Li and Na Deng and Xu Chen},
	title = {Level set medical image segmentation aided by cooperative quantum particle optimization with L{\'{e}}vy flights},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]D. Li, N. Deng, and X. Chen, “Level set medical image segmentation aided by cooperative quantum particle optimization with Lévy flights,” Vibroengineering PROCEDIA, vol. 28, pp. 93–98, Oct. 2019, doi: 10.21595/vp.2019.21054.

Copy IEEE

Copied to clipboard!

Li, Desheng, Na Deng, and Xu Chen. “Level Set Medical Image Segmentation Aided by Cooperative Quantum Particle Optimization with Lévy Flights.” Vibroengineering PROCEDIA 28 (October 19, 2019): 93–98. https://doi.org/10.21595/vp.2019.21054.

Copy Chicago

Copied to clipboard!

Level set medical image segmentation aided by cooperative quantum particle optimization with Lévy flights

Abstract

Highlights

1. Introduction

2. Review of LBF algorithm

2.1. The classic LBF algorithm

3. Our proposed algorithms

3.1. CQPSO-LF algorithm

3.2. CQPSO-LF aided LBF algorithm (LBF-CQPSO-LF)

4. Experimental results and analysis

5. Conclusions

References

Cited by

About this article

Related Articles