Revisiting the tangential oscillations of the tool to form the microrelief of the workpiece surface

1. Introduction

It is known that at normal turning the roughness of the machined surface is formed due to the axially moving of a cutting tip. The size and shape of machined surface micro-irregularities consisting of the residual ridges are determined by the feed rate and the shape of cutting point. The mechanism of surface roughness formation due to oscillating motion under the vibrational turning will differ significantly.

The method of vibrational turning with the use of tangential oscillations showed sufficient efficiency for treatment of materials by cutting. The main advantages provided by this method are the reduction of surface roughness, chip crushing and the reduction of cutting forces when turning the hard-to-cut materials and built-up surfaces.

2. Experiments

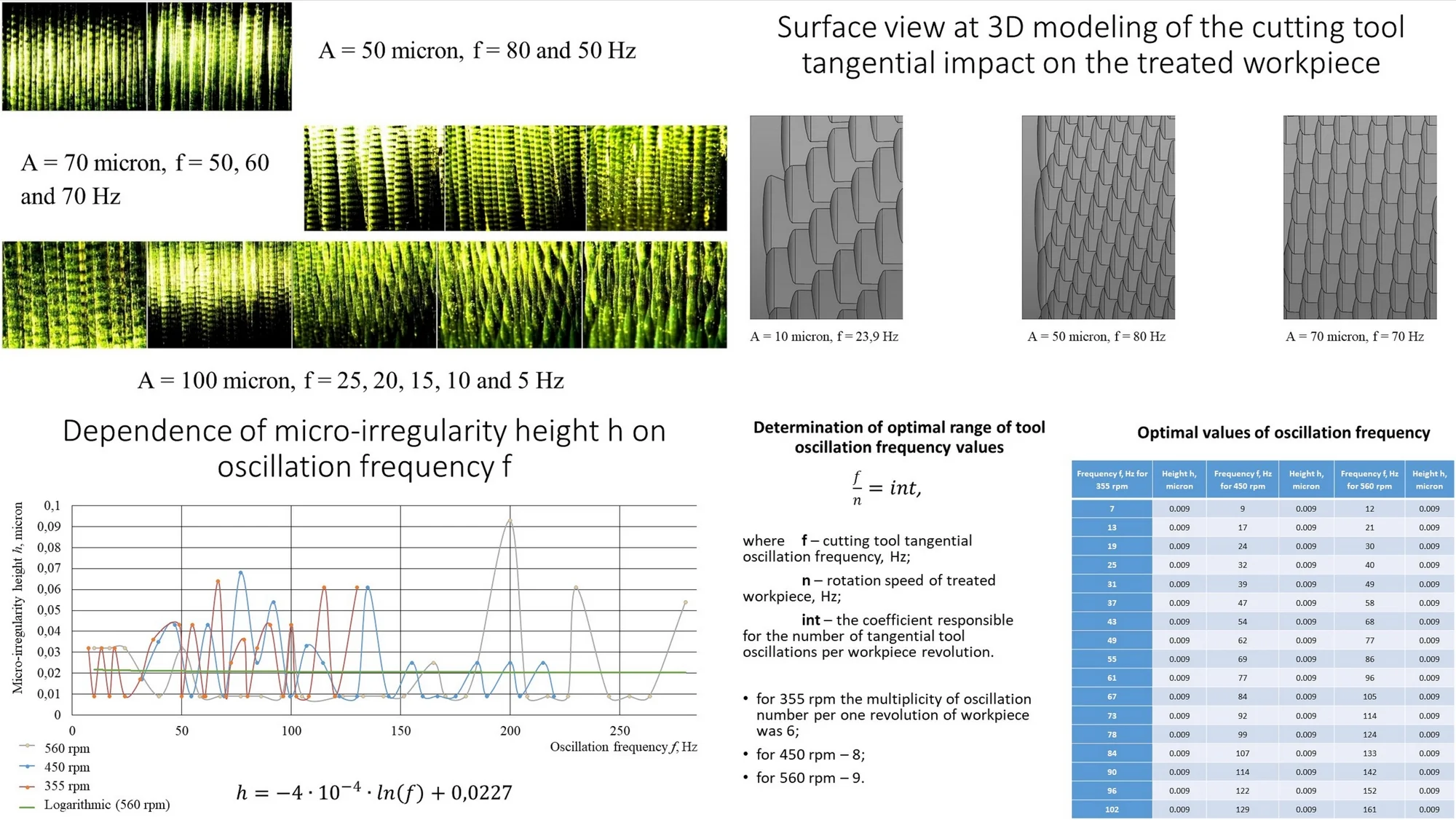
Vibrational turning with the imposition of tangential harmonic oscillations of pendulum type to the cutting tip includes two components: normal $A_r$ and tangential $A_{\tau }$. The trajectory of the cutting tip oscillations is explained by the conventional scheme presented on the Fig. 1.

The scheme of cutting tip trajectory change per one oscillation period presented on the Fig. 1 has shown that the main influence of the cutter oscillations on the treated surface is in tangential direction $A_{\tau }$, and auxiliary one in normal $A_r$. On the basis that the tangential component is equal to the amplitude of oscillations and the value of the tool overhang is known, the normal component of the oscillation amplitude can be found from a rectangular triangle, the calculation scheme of which is shown on Fig. 2 [1].

Various forms of machined surfaces microgeometry were obtained as a result of experiments on vibrational treatment of the workpieces. The traces of cutter oscillation in the form of radial scallops were noticed on the machined surface after vibrational turning. The length of scallops corresponds to the value of the vibration amplitude, and the width and radius in the cross-section depend on the geometric parameters of the tool Fig. 3 [2].

Fig. 1Cutting tip oscillation trajectory scheme

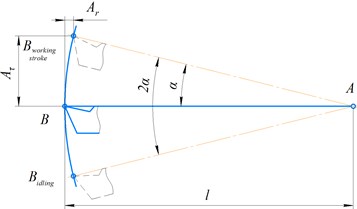
Fig. 2The conventional calculation scheme of tangential Aτ and normal Ar components of cutting tip oscillations

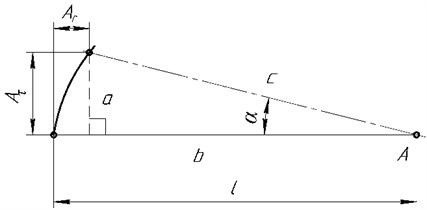
Fig. 3Traces of normal Ar and tangential Aτ components influence under various vibrational cutting modes: а) – sample No. 1; b) – sample No. 2; c) – sample No. 3

а) $A=$ 50 micron, $f=$ 80 and 50 Hz

b)$A=$ 70 micron, $f=$ 50, 60 and 70 Hz

c)$A=$ 100 micron, $f=$ 25, 20, 15, 10 and 5 Hz

3. Results

The use of vibrational turning method allows combining two schemes of surface roughness microgeometry on the machined surface which correspond to the longitudinal turning by the cutter and milling by the cylindrical mill Fig. 4 [3].

Fig. 4Machined surface micro-profile calculation scheme: а) under turning; b) under milling

a)

b)

Studying the influence of tool oscillations on surface roughness formation, it is necessary to consider two calculation schemes of roughness profile formation in the plane parallel and perpendicular to the workpiece axis Fig. 3. The first one reflects the movements of normal turning without the imposition of oscillations, the second one reflects the influence of cutter oscillation on the kinematics of cutting and corresponds to the scheme of surface roughness formation under the milling by a cylindrical mill. Imposition of these movements of the cutter in the space will lead to reduction of surface roughness in comparison with the turning without tool oscillations.

It is seen from the Fig. 3 that the surface after vibrational turning has a scale-shaped roughness.

It was established that the mechanism of the combined micro-profile formation of the machined surface exists at a certain correlation of amplitude-frequency parameters of tangential oscillations of the cutting tool and cutting modes. The modeling of such surface microgeometry form is possible with the help of 3D-modeling of tool motion kinematics.

The models of surfaces at various oscillation frequencies for the conducted experiments on vibrational turning were obtained by modeling in KOMPAS-3D program Fig. 5.

Fig. 5Surface view at 3D modeling of the cutting tool tangential impact on the treated workpiece: а) A= 10 micron, f= 23,9 Hz; b) A= 50 micron, f= 80 Hz; c) A= 70 micron, f= 70 Hz

а)

b)

c)

Based on the presented fragments of surface models acquired by modeling of vibrational turning, it is obvious that the surface is formed due to the complex mechanical impact of the cutting tool to the surface of the treated workpiece, including the longitudinal movement of the feed, tangential $A_{\tau }$ and normal $A_r$ component of oscillations. This type of influence forms a scale-shaped micro-profile on the workpiece with elements typical for both turning and milling. However, it should be noted that such character of surface micro-irregularities formation is possible only at certain combinations of cutting modes and amplitude-frequency characteristics of tangential pendulum oscillations.

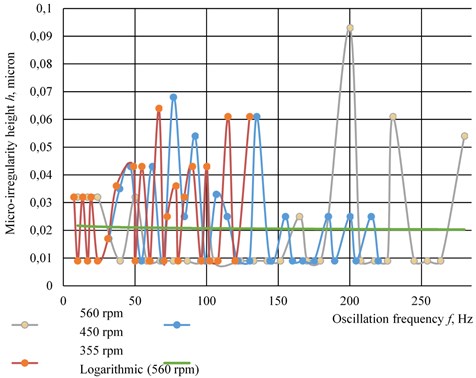
Based on achieved geometrical models of the surfaces, the graphs of surface roughness height $h$ dependence which has essential influence on roughness of surface $R_z$, on frequency of oscillations of the cutting tool $f$ Fig. 6, were made for three workpiece rotation speeds [2].

Analyzing the obtained dependencies, it should be noted that the values of oscillation frequencies can be divided into two groups: the first group corresponds to the maximum height of surface micro-irregularities and the second group which corresponds to the minimum height.

The logarithmic approximation represented by the Eq. (1) is the optimal mathematical method for determining as closely as possible the values of oscillation frequencies at which the height of micro-irregularity of the surface will be reduced to a minimum value:

It should also be noted that for each rotation speed of the workpiece it is necessary to determine its optimal range of oscillation frequency of the tool, at which the condition of obtaining the minimum height of surface micro-irregularities is observed. Determining the optimal oscillation frequency range comes to the use of such frequencies at which the number of cutting tool oscillations per one revolution of workpiece is a multiple of the defined integral value.

Fig. 6Dependence of micro-irregularity height h on oscillation frequency f

Determination of optimal range of tool oscillation frequency values was performed on the Eq. (2):

where $f$ – cutting tool tangential oscillation frequency, Hz; $n$ – rotation speed of treated workpiece, Hz; $int$ – the coefficient responsible for the number of tangential tool oscillations per workpiece revolution.

It should be noted that determination of oscillation number value on such dependence is possible under constant diameter of machined workpiece.

As a result of the dependence Eq. (2), multiple integers were obtained from which the optimal oscillation frequencies corresponding to the three frequencies of workpiece revolution can be calculated:

1) for 355 rpm the multiplicity of oscillation number per one revolution of workpiece was 6.

2) for 450 rpm – 8.

3) for 560 rpm – 9.

On the basis of the obtained multiples of oscillation frequencies and rotation speeds of the workpiece with the diameter of 50 mm, it is possible to calculate the table of optimal oscillation frequencies for the rotation speed of the workpiece 355, 450 and 560 rpm, at which the minimum height of surface micro-irregularities will be formed to Table 1.

The height of micro-irregularities $h=$ 0.009 micron is limit for these modes of surface microgeometry formation.

Thus, summarizing the results of surface modeling under vibrating turning, it is possible to formulate the following observations that both the amplitude of vibration and frequency have a significant impact on surface roughness. It should also be noted that the oscillation amplitude has an effect in a certain range, which cannot be said about the oscillation frequency, which at the constant amplitude has a greater influence on the surface micro-irregularities.

Therefore, it is possible to make an intermediate conclusion that based on the convenience of controlling the amplitude-frequency parameters of tangential oscillations, it would be appropriate to change the frequency of oscillations at the constant optimal amplitude.

Thus, for realization of complex influence of surface treatment modes and amplitude-frequency characteristics of tangential oscillations it is necessary to observe the minimum ratio of rotation speed of a workpiece and oscillations of the tool corresponding to the certain rotation speed of a workpiece.

Proceeding from the fact that the study of the surface layer and the formation of surface micro-irregularities refers to one of the most important quality indicators of any machine, it is possible to consider that the application of tangential oscillations of the tool for the formation of surface micro-geometry has a fundamental nature [4, 5].

The study of the tool tangential oscillations impact as a method of surface microgeometry formation is relevant.

4. Conclusions

The directions for further research of the tool tangential oscillations are formulated and consist in: 1) investigation of the tool tangential oscillation physical base impact on the formation of surface microgeometry; 2) correlation study of amplitude-frequency characteristics of tangential oscillations and kinematic parameters of treated workpiece motion; 3) feasibility study of tangential oscillation application for the formation of surface microgeometry during the machining and surface plastic deformation by smoothening.