Abstract
In order to explore the feasibility of the new type of armor against projectile penetration, a steel plate tube array composite armor was designed, and its effectiveness against projectile penetration was studied by numerical simulation. The results of simulation vividly reproduce the physical and mechanical processes of composite armor structure, such as deformation and breakage, penetration failure, and stress wave propagation under the impact of projectile. The time history characteristics of projectile residual velocity were accurately captured. The influence of key factors, such as the number of tube array layers, array combination form and projectile impact position on the damage mode of the composite armor structure was obtained. The related results can provide important support and scientific basis for the optimal design and accurate evaluation of the new composite armor.
Highlights
- In order to explore the feasibility of the new type of armor against projectile penetration, a steel plate tube array composite armor was designed
- the new designed armor's effectiveness against projectile penetration was studied by numerical simulation.
- The influence of key factors, such as the number of tube array layers, array combination form and projectile impact position on the damage mode of the composite armor structure was obtained.
1. Introduction
With the increasing attack efficiency of kinetic energy anti-armor weapons, the role of advanced armor protection in modern combat vehicles is becoming increasingly important. The development of armored structure to strong toughness, lightweight and composite is a significant trend direction. The metal tube shows good characteristics of absorbing energy and absorbing wave under shock load [1, 2]. In order to explore the application of metal tube in the field of armor protection, a new type of steel plate-tube array composite armor was designed.
The armor penetration problem under impact load is a complex nonlinear dynamic process. Numerical simulation technology is becoming more and more economical and efficient, which has become an important method to study the problem of armor penetration. In this paper, based on the dynamic nonlinear finite element program LS-DYNA3D [3], the damage response process of new armor forms of steel plate-tube array composite armor(SptAC armor) against high-speed rod projectile impact was simulated, and systematically analyzes the influence of the key factors such as the layer number of steel tube array, array combination form and impact position of projectile on the damage mode of composite armor structure against projectile impact, so as to provide important theoretical support and scientific basis for the optimal design and accurate evaluation of anti-ballistic performance of new composite armor.
2. Numerical simulation model
2.1. Basic assumptions
In this paper, the finite element numerical calculation model of projectile impact on SptAC armor structure is established, and the following assumptions and simplifications are made without affecting the calculation results: the influence of air resistance and gravity during projectile operation was ignored; the overall displacement of armor structure was not considered due to the short collision process; the steel plate, steel tube components and projectile materials in composite armor are uniform continuous medium.
2.2. Finite element model
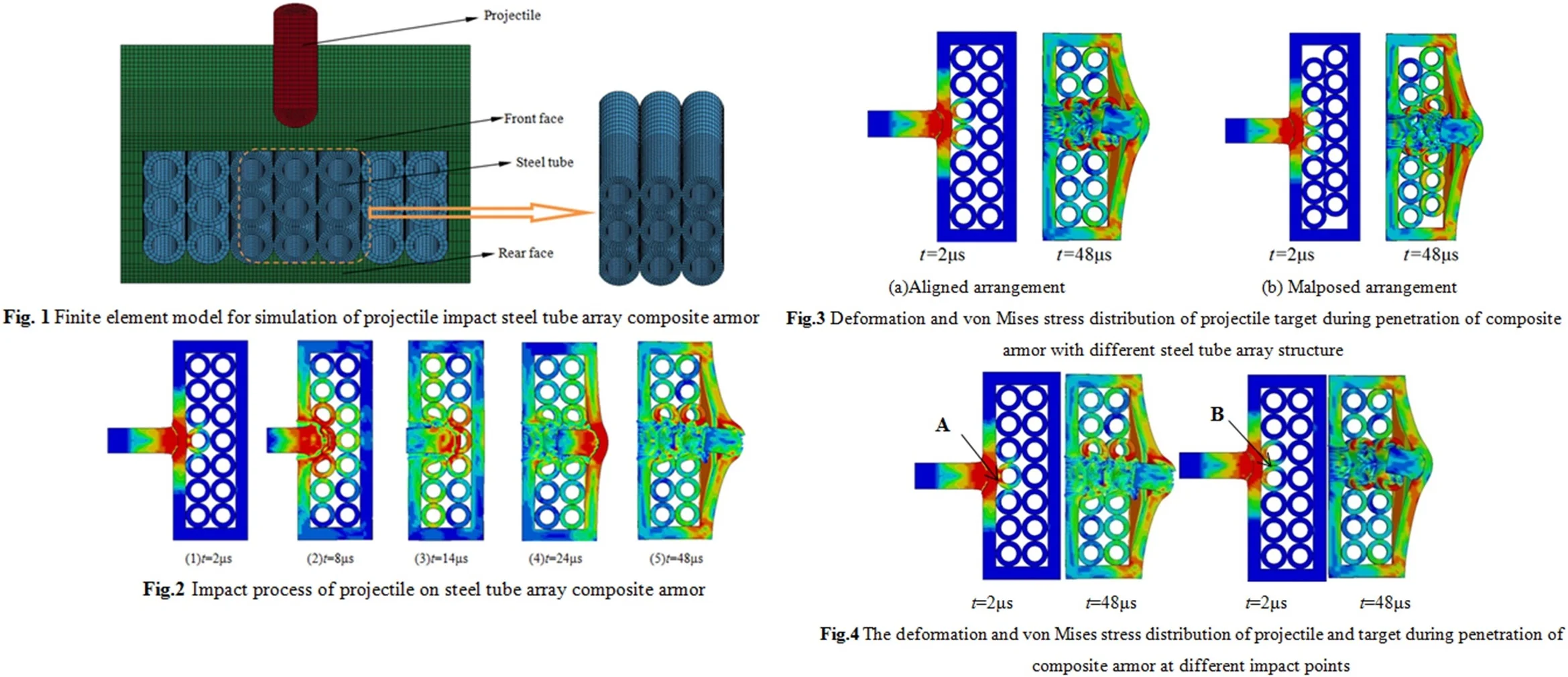
Obviously, the ballistic performance of the steel tube plate array is related to many factors, such as the material and size of the tube structure, the number of the tube, etc. In order to explore the feasibility of this kind of structure against projectile in advance, this paper fixed the size and number of tubes, and only considered the influence of tube layer number, arrangement mode and impact point position on projectile’s residual velocity and yaw. Fig. 1 shows the established finite element numerical model. There are two parts in finite element numerical model: the projectile, spherical head cylinder with a diameter of 2 mm, and slenderness ratio of 6 and a mass of 1.15 g; the armor, consist of 2 mm thickness target plate of the front, back and side face, and also the steel tube with 2 mm outer diameter and 1.2 mm inner diameter. Each layer of array is composed of seven steel tubes in contact. In view of the axisymmetric characteristics of projectile and target structure and load, a 1/2 model was established to save calculation time. Both the projectile and the target plate are made of solid 164 elements.
Fig. 1Finite element model for simulation of projectile impact steel tube array composite armor
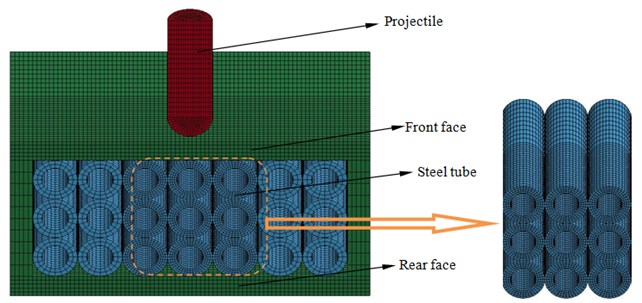
In order to improve the calculation speed and ensure the calculation accuracy, the mesh division is relatively fine in the contact area between projectile and target. The element number of projectile target plate and steel tube array were divided into 4000, 28500 and 57600 respectively. The boundary conditions were applied to the side of the target plate to simulate the fixed condition of the target plate, and symmetrical constraints are applied on the symmetrical boundary.
2.3. Material model and parameters
When the numerical simulation of SptAC armor was carried out, the projectile and composite target plate adopt the same type of steel material, namely Q235 steel. In order to better simulate the fracture and failure of composite target under projectile impact penetration, the Johnson cook material model with failure fracture criterion was selected for both projectile and target [4]:
For von Mises yield stress model, the material yield stress is expressed as follows:
where: is equivalent plastic strain, is relative equivalent plastic strain rate, is relative temperature, is yield stress, is strain hardening, is strain hardening index, is strain rate correlation factor, is temperature correlation factor.
The expression of the fracture strain is expressed as follows:
where is the damage to a material element, is the increment of accumulated plastic strain, and is the accumulated plastic strain to failure under the current conditions of stress triaxiality, strain rate and temperature. Failure occurs when 1. The material model parameters of Q235 steel are [5]: 7.8 g/cm3, 229.0 MPa, 439.0 MPa, 0.503, 0.1, 0.55, 0.3, 0.9, –2.8, 0.0, 0.0.
3. Damage effect of steel tube array composite armor against projectile impact
3.1. Projectile penetrating progress
Taking the two-layer aligned steel tube array composite armor as an example, Fig. 2 shows the deformation and von Mises stress distribution of projectile and target plate at different times during the impact penetration at the speed of 1000 m/s. The results show that at the moment of contact, the stress wave propagates from the contact point of the projectile to the projectile and the panel respectively. In a short time, the stress wave propagates rapidly through the steel tube. When 8 μs, the stress wave has reached the bottom of the projectile. At this time, the steel tube at the impact point has suffered severe deformation, and the steel tube side around had also undergone obvious buckling. After that, the stress wave continuously reflects and propagates back and forth in the projectile and composite target. When 24 μs, the two layers of steel tube have been completely damaged, and the projectile starts to act on the back plate, which causes serious deformation of the back plate. When 48 μs, the back plate had been penetrated. At the point of contact between the projectile and the composite target, the stress was always the maximum during the penetration process, the composite target plate seriously deformed, this is also the reason why the material of projectile and target at this point is easy to be penetrated and destroyed.
Fig. 2Impact process of projectile on steel tube array composite armor
a)2 μs
b)8 μs

c)14 μs
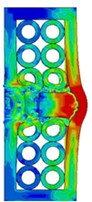
d)24 μs
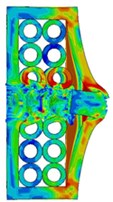
e)48 μs
3.2. Influence of layers number on anti-penetration performance of SptAC armor
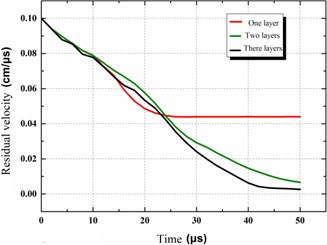
In order to study the effect of the layer number of the steel tube array on anti-penetration performance, the other parameter such as material and quality of the projectile and impact velocity were fixed. The values of the composite target plate of one layer, two layers and three layers of steel tube were calculated respectively. Fig. 3 shows the comparison of impact process of projectile on composite armor with different layers of steel tube array.
With the increase of the number of tube array layers, the anti-penetration ability of armor structure to projectile was significantly improved. On the one hand, with the increase of the number of steel tube array layers in the composite armor, the armor thickness that the projectile needs to penetrate was increased; on the other hand, when the number of steel tube array layers was large, the interaction time between the projectile and the composite armor increases, and the deformation energy absorption effect caused by the steel constraint was more significant, which makes the residual velocity of the projectile significantly reduced (as shown in Fig. 4).
Fig. 3Deformation and von Mises stress of projectile and armor with different layers at 48μs
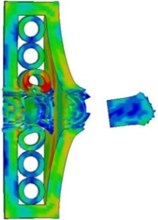
a) One layer
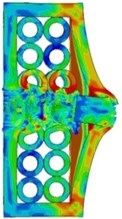
b) Double layers
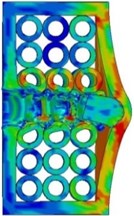
c) Three layers
Fig. 4Residual velocity curve of projectile under different layers of steel tube array
3.3. Influence of tube array relative position on anti-penetration performance of SptAC armor
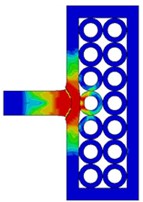
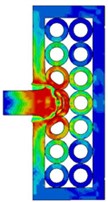
When the number of layers of steel tube array of composite armor is more than one layer, the array mode of each layer may have different forms, such as steel tube aligned arrangement and malposed arrangement between layers. Take the two-layer steel tube array composite armor as an example for simulation, as shown in Fig. 5.
The residual velocity and kinetic energy of projectile penetrating the composite armor with malposed arrangement structure decrease faster than those with aligned arrangement structure. When 20 μs, the residual velocity of projectile is 554 m/s in two-layer aligned arrangement structure and 533 m/s in two-layer malposed array structure. The reason is that in the malposed array structure, each steel tube contacts with four steel tubes, while in the aligned structure, each steel tube contacts only three steel tubes. Therefore, the malposed array structure can transfer more energy to the surrounding steel tube to absorb when the projectile and target collide and deform, so as to achieve better protection performance.
3.4. Influence of projectile initial position on anti-penetration performance of SptAC armor
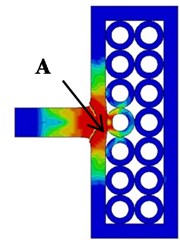
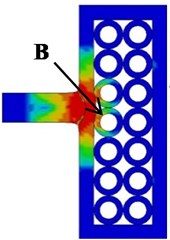
Keeps the same initial conditions as the simulation mentioned above. The impact point A (facing the center of the upper surface of the steel tube) and the impact point B (located in the middle of the adjacent steel tube) were numerically simulated (as shown in Fig. 6).
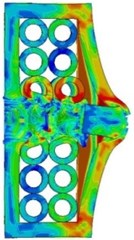
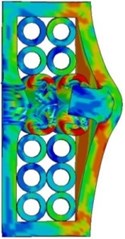
From the simulation results, for different steel tube array structures, the impact protection performance of composite armor for projectile is obviously different. When the projectile penetrates the composite armor at the impact point A, the residual velocity of the projectile is 66 m/s; when the projectile penetrates at the impact point B, the projectile velocity decreases to 0. The calculation results show that it is more difficult for the projectile to penetrate the composite target at the impact point B than at the impact point A when other conditions remain unchanged. Therefore, the dislocation array structure can transfer more energy to the surrounding steel tube to absorb when the projectile and target collide and deform, so as to achieve better protection performance.
Fig. 5Deformation and von Mises stress distribution of projectile target during penetration of composite armor with different steel tube array structure
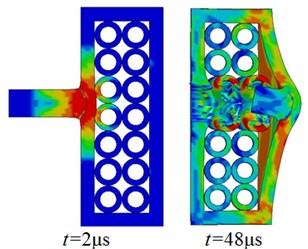
a) Aligned arrangement
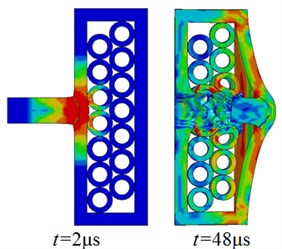
b) Malposed arrangement
Fig. 6The deformation and von Mises stress distribution of projectile and target during penetration of composite armor at different impact points
a)2 μs
b)48 μs
c)2 μs
d)48 μs
4. Conclusions
In order to explore the feasibility of SptAC armor against rod projectile’s penetration, a series of numerical simulation including effect analysis of some influencing factors were carried out, the conclusion are as follows:
1) The results of numerical simulation reproduce the physical and mechanical processes of composite armor structure, such as deformation and breakage, penetration failure, projectile abrasion and stress wave propagation under projectile impact.
2) Aiming at the composite armor of steel plate and steel tube array, the influence of the layers number, the combination form of tube array and projectile impact position on the ballistic performance of composite armor was studied. The results show that the steel tube array can significantly absorb the initial kinetic energy of the projectile through the bending plastic deformation, friction and collision between the steel tubes. The more layers and the staggered arrangement of the steel tube array are, the better the effect is. The energy absorption advantage of the projectile is more obvious when the target point is located between adjacent steel tubes.
References
-
Ji Chong, Long Yuan, Fang Xiang, et al. Dynamic response and perforation failure of shell subjected to lateral local impulsive loading. Journal of Vibration and Shock, Vol. 32, Issue 15, 2013, p. 121-125+137, (in Chinese).
-
Gao Fuyin, Long Yuan, Ji Chong, et al. Test for dynamic buckling modes of a metallic cylindrical shell subjected to lateral explosion. Journal of Vibration and Shock, Vol. 32, Issue 24, 2013, p. 117-121, (in Chinese).
-
Livermore Software Technology Corporation (LSTC). LS-DYNAR keyword user’s manual V971. Livermore, 2012.
-
Johnson G. R., Johnson G. R., Cook W. H., Johnson G., Cook W. A constitutive model and data for metals subjected to large strains, high strain-rates and high temperatures. 7th International Symposium on Ballistics, Hague, 1983, p. 541-547.
-
Xiao Xinke Anti-penetration performance of double metal target and deformation and fracture of Taylor bar. Harbin Institute of Technology, Harbin, 2010, (in Chinese).
About this article
This research was financially supported by the National Nature Science Foundation of China, Nos. 51978660 and 51678567.
