Mechanical characterization of bottom hole assembly in air drilling engineering

1. Introduction

Air drilling is an excellent technology for improving rate of penetration, which has been widely used in petroleum exploration and development [1]. However, many studies focused on the mechanism of well deviation by analyzing the mechanical behavior of drill string in mud drilling, but neglected the mechanism of well deviation in air drilling. A series of problems, such as the structure of bottom hole assembly (BHA), strata, expansion ratio of borehole diameter (ERBD) and wellbore instability, etc., are encountered in the process of practical drilling, which lead to more serious well deviation in air drilling than the conventional mud drilling. Therefore, it is essential to investigate the principle and control of well deviation in the air drilling [2-5]. Due to the mechanism of well deviation in the air drilling is less publicly reported, more findings of mechanism of well deviation focus on the mud drilling. In the early stage, the influences of drill collar and stabilizer on well deviation were studied based on the static analysis of drill string, and the mechanical model of drill string is simplified as Euler-Bernoulli beam [6, 7]. Hence, the drill string is considered as slender beams or variable cross-section beam in the mechanical analysis [8, 9]. Many scholars deemed that the main cause of well deviation is side force of BHA, then a thorough understanding of mechanical behavior of BHA is significant for controlling well deviation. For example, Millheim et al. [10] analyzed the static mechanics of BHA by the finite element method, and the well trajectory affected by dynamic behavior of BHA is also concerned; the finite element method is high accuracy to solve problems with irregular shapes and complex constraints of beam, but the computation efficiency is restricted by the complexity of finite element model of BHA. In addition, a mechanical model of prebent BHA with positive displacement motor was proposed, and side force of BHA affected by bend angle and rotational speed of drill-string is revealed [11]. To better investigate the mechanical behavior of BHA, the downhole string bucking behavior was analyzed [12-14]. Besides, the weighted margin method is given to analyze the three-dimensional mechanical characteristics of BHA with small deflection. Zhang and Di et al. [15] applied the weighted margin method to determine the upper tangent point through a nonlinear static model of BHA. The methods above are applied widely to explore the mechanical properties of BHA in mud drilling, which may provide research ideas and schemes for exploring the mechanism of well deviation in the air drilling.

On the other hand, well deviation is significantly influenced by strata situation, such as stratigraphic anisotropy index, rock characteristics, wellbore instability and the interaction between bit and rock, etc. [16, 17]. The concept of stratigraphic anisotropy index was firstly proposed by Lubinski and Woods, who analyzed the rock properties affecting on well deviation [6]. Based on Lubinski’s theory, Merphey et al. [18] proposed deviating force of strata, and the relationship between deviating force of strata and WOB was determined; however, the model is unsuitable for gravel strata. With the development of drilling technology, a simple equation for calculating deviating force of strata was obtained according to the filed experience, but the effect of drill bit on deviating force of strata was neglected [19]. Su et al. [20] considered the cutting anisotropic index of bit in a new model of deviating force of strata, and the influences of strata dip and rock anisotropic index on deviating force of strata were discussed. To further investigate the bit affecting on deviating force of strata, Dai et al. [21] presented a model of deviating force of strata considering the anisotropy and tilt angle of bit, which can properly apply to evaluate drifting characteristics of strata in practice. However, the above models of deviating force of strata are established in mud drilling, and the models in air drilling and gravel strata are rarely considered; different with mud drilling and general strata, the deviating force of strata affected by the parameters related to BHA and gravel strata will be revealed in this paper.

In this article, mechanical models of BHA and gravel strata are proposed to predict the inclination and azimuth of borehole trajectory in air drilling. The mechanical model of BHA is established by utilizing the beam-column method in Section 2. To better predict the borehole trajectory, the deviating force model of gravel strata is considered in Section 3. The side force of BHA and deviating force of gravel strata is numerically computed in Section 4. Experimental verification is compared with the theoretical analysis. Finally, the conclusions are briefly summarized in Section 6.

2. Mechanical model of BHA with double stabilizer

2.2. Mechanical model

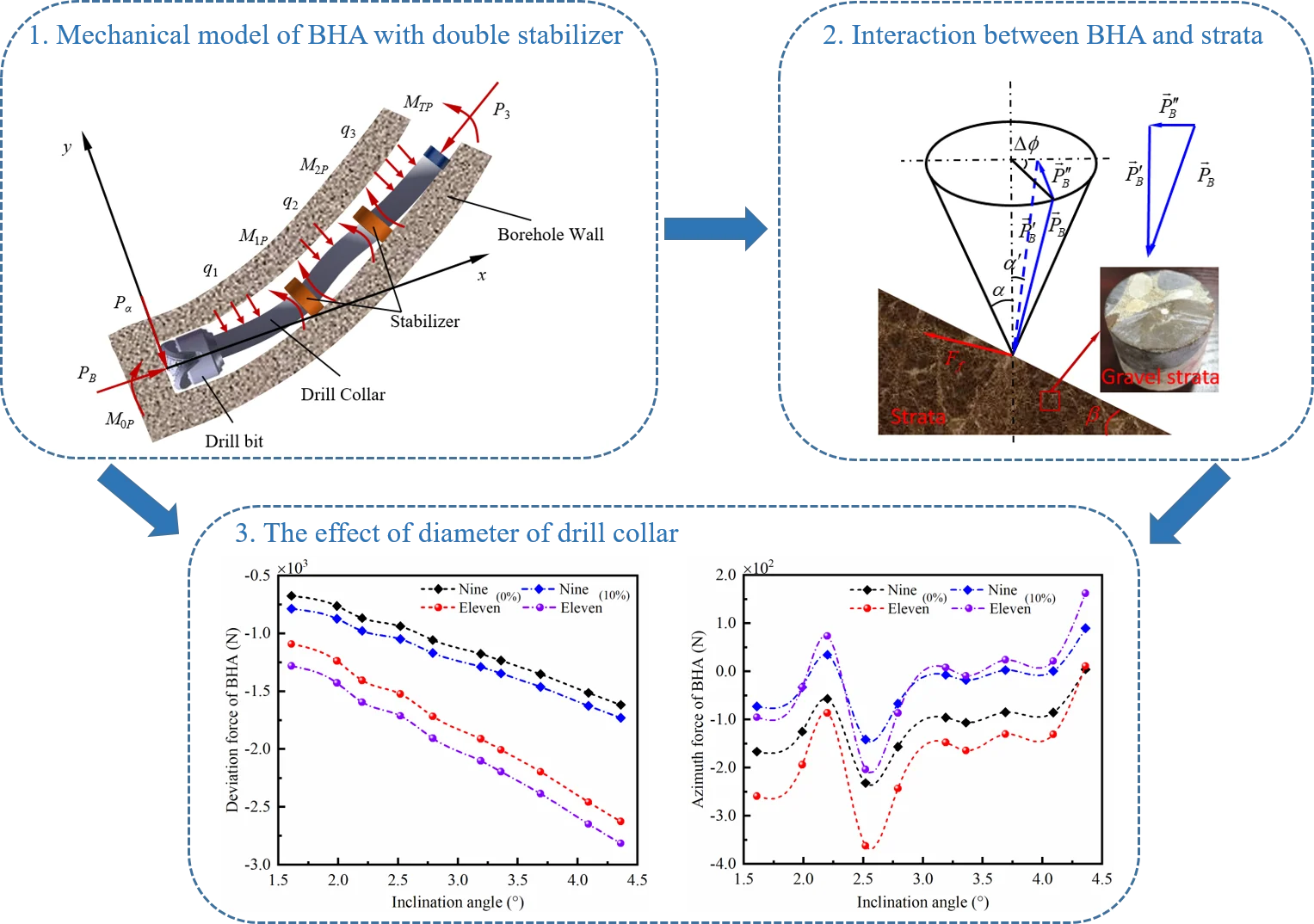
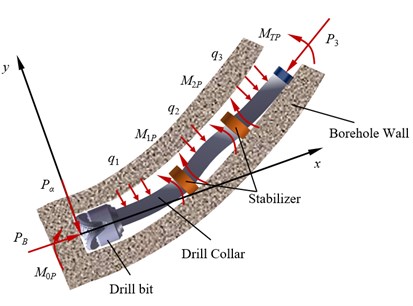
The borehole trajectory in the actual drilling engineering is a three-dimensional space curve. Therefore, the forces of BHA in well bottom are affected by the inclination and azimuth angle of borehole trajectory. For analyzing the mechanical characteristics of BHA in the three-dimensional borehole, the mechanical model of BHA in three-dimensional space can be transformed to force analysis of BHA in the two planes. One of plane represents the deviation plane, and the other represents the azimuth plane. Hence, the side force of BHA can be decomposed into deviation force and azimuth force. To establish the mechanical model of BHA with double stabilizer, the contacts among bit, stabilizer and borehole wall can be regarded as hinge support. Furthermore, the center line of BHA is assumed to be a smooth curvature with small deflection in three-dimensional space. In addition, the axis line of drill collar is overlapped with the borehole trajectory. Finally, the BHA in the mechanical model is separated three span beams in the places of the bit, stabilizers and upper tangent point, in this case, the beams are subjected to the longitudinal and lateral loads.

Fig. 1Mechanical model of BHA with double stabilizer

a) The deviation plane

b) The azimuth plane

Fig. 1(a) shows the forces of BHA with double stabilizer in the well deviation plane. $M_{1P}$ and $M_{2P}$ represent the additional internal bending moment of the two stabilizers, respectively. $M_{0P}$ is the bending moment at the bit. $M_{TP}$ is the bending moment of BHA at the upper tangent point, i.e.:

1

$M_{TP}=E{I}_3{K}_P,$

where, $K_P$ expresses the curvature of borehole trajectory in the well deviation plane, $E{I}_3$ represents the bending stiffness of the third span of drill collar.

Transverse uniform load $q_i$ ($i=$1, 2, 3), generated by gravity of drill collar, is constant in every span, i.e.:

2

$q_i={\omega }_i\mathrm{s}\mathrm{i}\mathrm{n}{\left({\alpha }_i\right)}_m,$

with:

${\omega }_i=\left({\rho }_1\frac{R_i^2-r_i^2}{4}+{\rho }_2\frac{r_i^2}{4}\right)\pi g,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}{\left({\alpha }_i\right)}_m={\alpha }_0-K_P\sum _{i=1}^i{L}_i+\frac{K_P{L}_i}{2},$

where, ${\omega }_i$ ($i=$1, 2, 3) represents the line weight of the $i$-th span drill collar, and ${\left({\alpha }_i\right)}_m$($i=$1, 2, 3) expresses well inclination angle in the midpoint of the $i$-th span drill collar. In addition, ρ₁ and ${\rho }_2$ depict the density of drill collar and compressed air, respectively. $R_i$ ($i=$1, 2, 3) and $r_i$ ($i=$1, 2, 3) represent the outer and inner diameters of the $i$-th span drill collar, respectively. Besides, $L_i$ ($i=$1, 2, 3) represents the length of the $i$-th span of drill collar.

$P_B$ is the weight of drill string on bit, the axial force $P_{iP}$ ($i=$1, 2, 3) of each span is denoted as:

3

$P_{iP}=P_B-\sum _{j=1}^i{\omega }_j{L}_j\mathrm{c}\mathrm{o}\mathrm{s}{\left({\alpha }_j\right)}_m+\frac{{\omega }_i{L}_i\mathrm{c}\mathrm{o}\mathrm{s}{\left({\alpha }_i\right)}_m}{2}.$

According to the moment balance of the first span of drill collar, the deviation force $P_{\alpha }$ can be given as:

4

$P_{\alpha }=-\left(\frac{P_B{y}_{1P}}{L_1}+\frac{q_1{L}_1}{2}+\frac{M_{1P}-M_{0P}}{L_1}\right).$

Based on the superposition principle of supported beam, the rotation angle at both ends of the drill collar is obtained by:

5

$\left\{\begin{array}{l}{\theta }_{1P}^R=\frac{q_1{L}_1^3}{24E{I}_1}X\left(u_{1P}\right)+\frac{M_{1P}{L}_1}{3E{I}_1}Y\left(u_{1P}\right)+\frac{M_{0P}{L}_1}{6E{I}_1}Z\left(u_{1P}\right)+\frac{y_{1P}-y_{0P}}{L_1},\\ {\theta }_{2P}^L=\frac{q_2{L}_2^3}{24E{I}_2}X\left(u_{2P}\right)+\frac{M_{1P}{L}_2}{3E{I}_2}Y\left(u_{2P}\right)+\frac{M_{2P}{L}_2}{6E{I}_2}Z\left(u_{2P}\right)-\frac{y_{2P}-y_{1P}}{L_2},\\ {\theta }_{2P}^R=\frac{q_2{L}_2^3}{24E{I}_2}X\left(u_{2P}\right)+\frac{M_{2P}{L}_2}{3E{I}_2}Y\left(u_{2P}\right)+\frac{M_{1P}{L}_2}{6E{I}_2}Z\left(u_{2P}\right)+\frac{y_{2P}-y_{1P}}{L_2},\\ {\theta }_{3P}^L=\frac{q_3{L}_3^3}{24E{I}_3}X\left(u_{3P}\right)+\frac{M_{2P}{L}_3}{3E{I}_3}Y\left(u_{3P}\right)+\frac{M_{3P}{L}_3}{6E{I}_3}Z\left(u_{3P}\right)-\frac{y_{3P}-y_{2P}}{L_3},\\ {\theta }_{3P}^R=\frac{q_3{L}_3^3}{24E{I}_3}X\left(u_{3P}\right)+\frac{M_{3P}{L}_3}{3E{I}_3}Y\left(u_{3P}\right)+\frac{M_{2P}{L}_3}{6E{I}_3}Z\left(u_{3P}\right)+\frac{y_{3P}-y_{2P}}{L_3},\end{array}\right.$

with:

$\left\{\begin{array}{l}{e}_0=\frac{D_w-D_b}{2},\\ e_1=\frac{D_w-D_{s1}}{2},\\ e_2=\frac{D_w-D_{s2}}{2},\\ e_3=\frac{D_w-D_{c3}}{2},\end{array}\right.\left\{\begin{array}{l}{y}_{0P}=e_0,\\ y_{1P}=\frac{K_P{L}_1^2}{2}-e_1,\\ y_{2P}=\frac{K_P{\left(L_1+L_2\right)}^2}{2}-e_2,\\ y_{3P}=\frac{K_P{\left(L_1+L_2+L_3\right)}^2}{2}-e_3,\end{array}\right.\left\{\begin{array}{l}X\left(u_i\right)=\frac{3}{u_i^3}\left(\mathrm{t}\mathrm{a}\mathrm{n}{u}_i-u_i\right),\\ Y\left(u_i\right)=\frac{3}{2u_i}\left(\frac{1}{2u_i}-\frac{1}{\mathrm{t}\mathrm{a}\mathrm{n}2u_i}\right)\\ Z\left(u_i\right)=\frac{3}{u_i}\left(\frac{1}{\mathrm{s}\mathrm{i}\mathrm{n}2u_i}-\frac{1}{2u_i}\right),\end{array}\right.,$

where,$u_i$ represents the stability factor of beam, $u_i=\sqrt{P_i{L_i}^2/4E{I}_i}$. $X\left(u_i\right)$, $Y\left(u_i\right)$ and $Z\left(u_i\right)$ represent amplification factors of the beam. $y_{iP}$ ($i=$0, 1, 2, 3) represents the ordinate at the end of beam. $e_0$, $e_1$, $e_2$ and $e_3$ represent the radial clearance from bit, the first stabilizer, the second stabilizer and the third drill collar to well wall, respectively. $D_w$, $D_b$, $D_{s1}$, $D_{s2}$ and $D_{c3}$ represent the diameters of the borehole, the bit, the first stabilizer, the second stabilizer and the third drill collar, respectively.

By utilizing the condition of public tangent at the stabilizers, the continuity condition at the two stabilizers is obtained as:

6

$\left\{\begin{array}{l}{\theta }_{1P}^R=-{\theta }_{2P}^L,\\ {\theta }_{2P}^R=-{\theta }_{3P}^L.\end{array}\right.$

The boundary condition at upper tangent point can be depicted as:

7

${\theta }_{3P}^R={\theta }_{TP}=K_P\left(L_1+L_2+L_3\right).$

Considering the continuity condition and the boundary condition, the three-moment equation of BHA with double stabilizer in the well deviation plane is derived based on three-moment theory of longitudinal and transverse continuous beams. The three-moment equation can be expressed as:

8

$\begin{array}{l}{M}_{0P}Z\left(u_{1P}\right)+2M_{1P}\left[Y\left(u_{1P}\right)+\frac{L_2{I}_1}{L_1{I}_2}Y\left(u_{2P}\right)\right]+M_{2P}\frac{L_2{I}_1}{L_1{I}_2}Z\left(u_{2P}\right)\\ =-\frac{q_1{L}_1^2}{4}X\left(u_{1P}\right)-\frac{q_2{L}_2^3{I}_1}{4L_1{I}_2}X\left(u_{2P}\right)-\frac{6E{I}_1}{L_1}\left[\frac{y_{1P}-y_{0P}}{L_1}-\frac{y_{2P}-y_{1P}}{L_2}\right],\end{array}$

9

$\begin{array}{l}{M}_{1P}Z\left(u_{2P}\right)+2M_{2P}\left[Y\left(u_{2P}\right)+\frac{L_3{I}_2}{L_2{I}_3}Y\left(u_{3P}\right)\right]+M_{3P}\frac{L_3{I}_2}{L_2{I}_3}Z\left(u_{3P}\right)\\ =-\frac{q_2{L}_2^2}{4}X\left(u_{2P}\right)-\frac{q_3{L}_3^3{I}_2}{4L_2{I}_3}X\left(u_{3P}\right)-\frac{6E{I}_2}{L_2}\left[\frac{y_{2P}-y_{1P}}{L_2}-\frac{y_{3P}-y_{2P}}{L_3}\right],\end{array}$

10

$q_{3}X\left(u_{3P}\right)L_3^4+4\left[2M_{3P}Y\left(u_{3P}\right)+M_{2P}Z\left(u_{3P}\right)\right]L_3^2=24E{I}_3\left[L_3\left(L_1+L_2+L_3\right)K_P+y_{2P}-y_{3P}\right].$

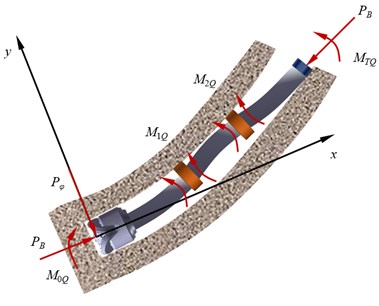
Fig. 1(b) shows the forces of BHA with double stabilizer in the azimuth plane. The gravity effect of drill string is all acting on the well deviation plane, therefore, lateral loads caused by drill collar gravity are neglected in the azimuth plane. Furthermore, the axial forces in every span of drill collar are equal to WOB. The bending moment $M_{TQ}$ at the upper tangent point in the azimuth plane can be expressed as:

11

$M_{TQ}=E{I}_3{K}_Q,$

where $K_Q$ is the curvature of borehole in the azimuth plane.

On the basis of theoretical analysis, the axial force $P_{iQ}$ ($i=$1, 2, 3) of each span can be given as:

12

$P_{iQ}=P_B.$

In addition, the azimuth force $P_{\phi }$ at the bit is derived as:

13

$P_{\phi }=-\left(\frac{P_B+M_{1Q}-M_{0Q}}{L_1}\right).$

Different with the well deviation plane, the rotation angle at both ends of drill collar in the azimuth plane can be expressed as:

14

$\left\{\begin{array}{l}{\theta }_{1Q}^R=\frac{M_{1Q}{L}_1}{3E{I}_1}Y\left(u_{1Q}\right)+\frac{M_{0Q}{L}_1}{6E{I}_1}Z\left(u_{1Q}\right)+\frac{y_{1Q}-y_{0Q}}{L_1},\\ {\theta }_{2Q}^L=\frac{M_{1Q}{L}_2}{3E{I}_2}Y\left(u_{2Q}\right)+\frac{M_{2Q}{L}_2}{6E{I}_2}Z\left(u_{2Q}\right)-\frac{y_{2Q}-y_{1Q}}{L_2},\\ {\theta }_{2Q}^R=\frac{M_{2Q}{L}_2}{3E{I}_2}Y\left(u_{2Q}\right)+\frac{M_{1Q}{L}_2}{6E{I}_2}Z\left(u_{2Q}\right)+\frac{y_{2Q}-y_{1Q}}{L_2},\\ {\theta }_{3Q}^L=\frac{M_{2Q}{L}_3}{3E{I}_3}Y\left(u_{3Q}\right)+\frac{M_{3Q}{L}_3}{6E{I}_3}Z\left(u_{3Q}\right)-\frac{y_{3Q}-y_{2Q}}{L_3},\\ {\theta }_{3Q}^R=\frac{M_{3Q}{L}_3}{3E{I}_3}Y\left(u_{3Q}\right)+\frac{M_{2Q}{L}_3}{6E{I}_3}Z\left(u_{3Q}\right)+\frac{y_{3Q}-y_{2Q}}{L_3},\end{array}\right.$

with:

$\left\{\begin{array}{l}{y}_{0Q}=e_0,\\ y_{1Q}=\frac{K_Q{L}_1^2}{2}+e_1,\\ y_{2Q}=\frac{K_Q{\left(L_1+L_2\right)}^2}{2}+e_2,\\ y_{3Q}=\frac{K_Q{\left(L_1+L_2+L_3\right)}^2}{2}-e_3.\end{array}\right.$

The continuity condition of rotation angle in the azimuth plane can be indicated as:

15

$\left\{\begin{array}{l}{\theta }_{1Q}^R=-{\theta }_{2Q}^L,\\ {\theta }_{2Q}^R=-{\theta }_{3Q}^L.\end{array}\right.$

The boundary condition in the azimuth plane can be depicted as:

16

${\theta }_{3Q}^R={\theta }_{TQ}=K_Q\left(L_1+L_2+L_3\right).$

The three-moment equation of BHA with double stabilizer in the azimuth plane can be established by adopting the same principle of the well deviation plane. Therefore, the three-moment equation in the azimuth plane is represented as:

17

$M_{0Q}Z\left(u_{1Q}\right)+2M_{1Q}\left[Y\left(u_{1Q}\right)+\frac{L_2{I}_1}{L_1{I}_2}Y\left(u_{2Q}\right)\right]+M_{2Q}\frac{L_2{I}_1}{L_1{I}_2}Z\left(u_{2Q}\right)=-\frac{6E{I}_1}{L_1}\left[\frac{y_{1Q}-y_{0Q}}{L_1}-\frac{y_{2Q}-y_{1Q}}{L_2}\right],$

18

$M_{1Q}Z\left(u_{2Q}\right)+2M_{2Q}\left[Y\left(u_{2Q}\right)+\frac{L_3{I}_2}{L_2{I}_3}Y\left(u_{3Q}\right)\right]+M_{3Q}\frac{L_3{I}_2}{L_2{I}_3}Z\left(u_{3Q}\right)=-\frac{6E{I}_2}{L_2}\left[\frac{y_{2Q}-y_{1Q}}{L_2}-\frac{y_{3Q}-y_{2Q}}{L_3}\right],$

19

$\left[2M_{3Q}Y\left(u_{3Q}\right)+M_{2Q}Z\left(u_{3Q}\right)\right]L_3^2=6E{I}_3\left[L_3\left(L_1+L_2+L_3\right)K_Q+y_{2Q}-y_{3Q}\right].$

3. Deviating force of strata

The well deviation is mainly caused by the imbalance of side force of BHA and deviating force of strata. When the sum of deviating force between BHA and strata is equal to zero, angle of well inclination is maintained; when the sum is more than zero, angle of well inclination is increased; when the sum is smaller than zero, angle of well inclination is decreased. Therefore, deviating force of strata is another key factor to affect the well deviation. According to Bai’s analysis [8], WOB cannot be considered a plane force during the drilling process, which leads to the variations of deviation and azimuth angle of well trajectory. Hence, there is an azimuth difference between the vertical plane where the WOB is located and the strata profile. The deviating force of strata produced by WOB not only causes the change of well deviation, but also leads to the variation of azimuth. The WOB can be applied in the vertical plane, and the angle between vertical plane and strata profile is considered as $\mathrm{\Delta }\varphi$, as shown in Fig. 2(a). As $\mathrm{\Delta }\varphi$ is changed in range of [0, 2$\pi$] considering different well azimuth in the drilling process, the WOB is actually an elliptic cone with deviation angle $\alpha$. The cone angle represents the angle of well inclination, and the bus length of the elliptic cone is the value of WOB.

The WOB $P_B$ is decomposed into $P_B^{\text{'}}$ and $P_B^{\text{'}\text{'}}$. $P_B^{\text{'}\text{'}}$is only considered compaction function on strata along to strata strike, and other functions are ignored. The component $P_B^{\text{'}}$ is located within strata profile, the angle between $P_B^{\text{'}}$ and center line of the elliptic cone is ${\alpha }^{\text{'}}$. The deviating force of strata is generated in the strata profile [8], which can be expressed as:

where $\beta$ is the dip angle of strata, $H$ is the comprehensive cutting anisotropy index; besides, the comprehensive cutting anisotropy index is determined by well inclination angle, dip angle of strata, anisotropy of rock and anisotropic cutting property of bit.

Fig. 2Interaction between BHA and strata

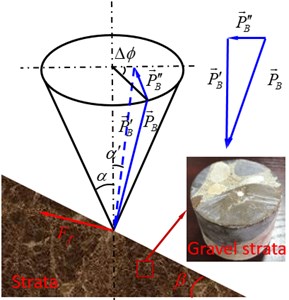
a) Theoretical model of WOB cone

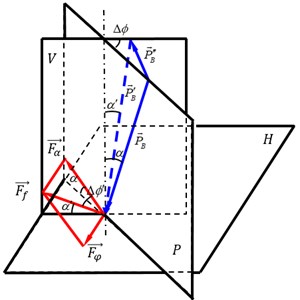
b) Analysis of deviating force of strata

The deviating force of strata is shown in Fig. 2(b), which is decomposed into the deviation force $F_{\alpha }$ in the well deviation plane and the azimuth force $F_{\phi }$ in the azimuth plane. In addition, the relationship between ${P\text{'}}_B$ and $P_B$ can be determined as:

where $\alpha$ is the angle of well inclination, $\mathrm{\Delta }\varphi$ denotes the azimuth difference.

$\mathrm{\Delta }\varphi \text{'}$ is actually the angle between deviation force $F_{\alpha }$ and resultant force $F_f$ of strata, which is indicated as:

The relationship among strata forces $F_f$, the deviation force of strata and the azimuth force of strata $F_{\phi }$ can be established as:

When $F_{\alpha }$ is greater than and less than zero, the angle of well deviation is increased and decreased, respectively; when $F_{\phi }$ is greater than and less than zero, the azimuth is drifted right and left, respectively.

4. Numerical computations

4.1. Side force of BHA

In this section, deviation force and azimuth force of BHA are discussed with different ERBD, WOB, angle of well inclination, diameter of drill collar and strata bending moment. The used BHA consists of Φ311.2 mm three-cone bit + Φ279.4 mm drill collar + Φ305 mm stabilizer + Φ228.6 mm drill collar + Φ308 mm stabilizer + Φ228.6 mm drill collar + Φ203.2 mm drill collar + Φ149.2 mm heavy weight drill pipe. In addition, some basic parameters of BHA are listed in Table 1.

Table 1Drilling parameters of BHA

No.	Parameters	Unit	Value
1	First stabilizer dimension ($D_{s1}$)	mm	305
2	Second stabilizer dimension ($D_{s2}$)	mm	308
3	Borehole diameter ($D_w$)	mm	311.2
4	Bit diameter ($D_b$)	mm	311.2
5	Young’s modulus ($E$)	GPa	206
6	WOB ($P_B$)	kN	10-40
7	Density of drill collar (${\rho }_1$)	kg/m3	6256
8	Air density (${\rho }_2$)	kg/m3	50
9	Length of first span ($L_1$)	m	19
10	Length of second span ($L_2$)	m	9
11	Linear weight of first span (${\omega }_1$)	kg/m	355
12	Linear weight of second span (${\omega }_2$)	kg/m	277
13	Linear weight of third span (${\omega }_3$)	kg/m	277
14	Principal moment of inertia of first span ($I_1$)	m4	2.97×10-4
15	Principal moment of inertia of second span ($I_2$)	m4	1.32×10-4
16	Principal moment of inertia of third span ($I_3$)	m4	1.32×10-4

4.1.1. The effect of ERBD

To clarify the difference of borehole diameter between mud drilling and air drilling, three adjacent wells in the same geological area are applied with mud drilling and air drilling, respectively. Due to lack of mud pressure support, the stability of wellbore with air drilling is weaker than mud drilling.

Fig. 3Expansion ratio of borehole diameter by air drilling

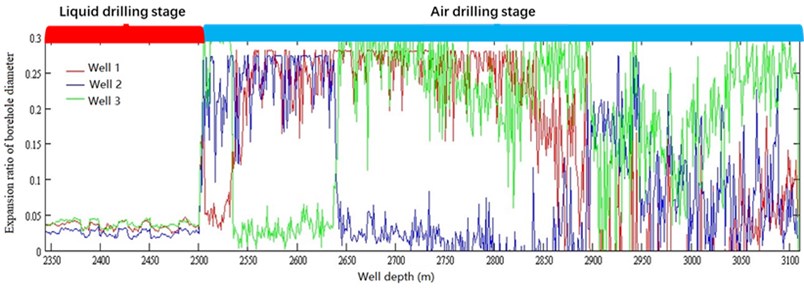
As shown in Fig. 3, it can be seen that the ERBD is ranged from 0.02 to 0.045 with mud drilling; however, the ERBD with air drilling, ranged from 0 to 0.3, is far larger than the mud drilling. Therefore, to explore the bit side force affected by ERBD, the ERBD is chosen as 0, 10 %, 20 % and 30 % according to the Fig. 3, respectively. The effect of ERBD on bit side force is discussed in light of numerical computation for Eqs. (1-19). When $P_B=$ 20 kN, the deviation force of BHA is shown in Fig. 4(a); the deviation force of BHA is obviously affected by different ERBD; and the larger ERBD, the better ability of reducing well deviation of BHA. In Fig. 4(b), the azimuth force is increased with the ERBD; however, when ERBD is 10 %, the azimuth force of BHA is changed to positive from negative in range of inclination angle from 1.5° to 2.5°, and then returned to negative in range of inclination angle from 2.5° to 4.5°. In this case, the increasing azimuth and decreasing azimuth of well trajectory are both existed in the drilling process. In addition, when ERBD is equal to 0 % and 30 %, the increasing azimuth and decreasing azimuth of well trajectory are appeared, respectively. The symbol of azimuth force represents the drift direction of azimuth; when azimuth force is negative, the azimuth is drifted to the left; however, when azimuth force is positive, the azimuth is drifted to the right. Thus, the side force of BHA is determined by ERBD and angle of well inclination in air drilling.

Fig. 4Influence of ERBD on bit side force

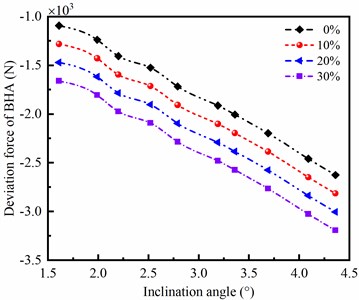
a) Deviation force of BHA

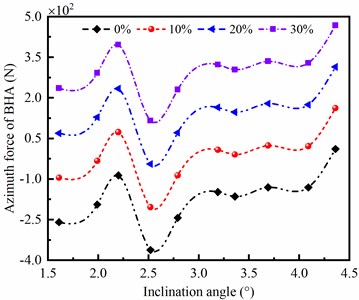
b) Azimuth force of BHA

4.1.2. The effect of WOB

The WOB used in air drilling is usually ranged from 10 kN to 40 kN. In this section, the WOB affecting on side force of BHA is discussed when the ERBD is 10 %. As shown in Fig. 5, It is obviously observed that the deviation force and azimuth force of BHA are little affected by the variation of WOB. However, the deviation force and azimuth force are obviously influenced by the angle of well inclination. Therefore, the side force of BHA is insensitive to WOB, but sensitive to angle of well inclination.

Fig. 5Influence of WOB on bit side force

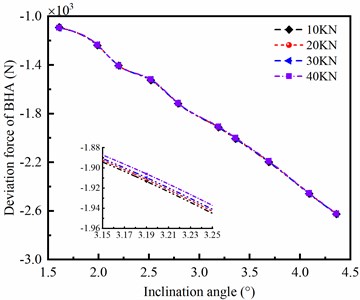
a) Deviation force of BHA

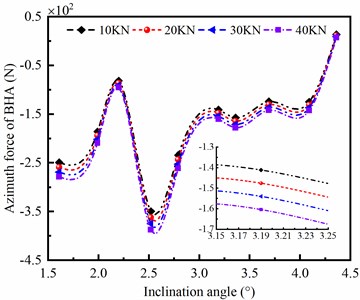
b) Azimuth force of BHA

4.1.3. The effect of diameter of drill collar

Drill collars with different outer diameter in same length are appeared as different bending stiffness; and the larger outer diameter, the stronger bending stiffness of drill collar. According to the mechanical model of BHA, it can be found that the stiffness and mass of drill collar are important factors affecting on the side force of bit. When the diameters of drill collar are nine and eleven inches, respectively, the deviation force of BHA is shown in Fig. 6(a). It can be seen that the deviation force of BHA is significantly influenced by the outer diameter of drill collar; and the larger diameter of drill collar, the bigger reducing deviation force of BHA. In Fig. 6(b), the azimuth force of BHA is increased with outer diameter of drill collar when ERBD is assumed as 0 %; however, when ERBD is 10 %, the azimuth force of BHA with nine-inch drill collar is larger than eleven inch near the inclination angle of 2°. Therefore, the large outer diameter of drill collar is beneficial to decrease the well deviation, but exacerbates the azimuth drift of well trajectory.

Fig. 6Influence of diameter of drill collar on bit side force

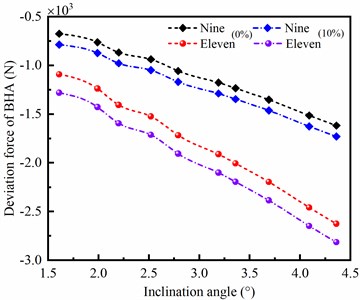
a) Deviation force of BHA

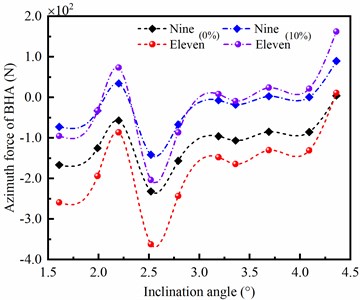
b) Azimuth force of BHA

4.1.4. The effect of strata bending moment

If the drilled strata are sophisticated in the drilling process, such as gravel strata in Fig. 2(a), the reaction force of strata on the BHA may be deviated from drill axis on account of strong heterogeneity of the gravel stratum, which leads to the existence of strata bend moment in contact between the bit and rock. Thus, it is essential to explore the effect of strata bending moment on the side force of bit.

Fig. 7Influence of strata bending moment on bit side force

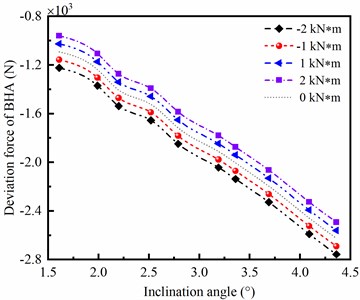
a) Deviation force of BHA

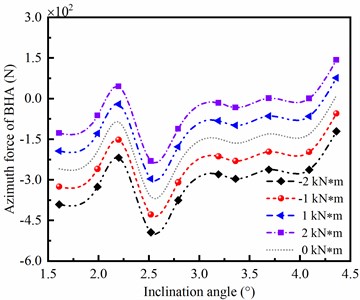
b) Azimuth force of BHA

As shown in Fig. 7(a), it can be seen that the deviation force of BHA is decreased with the increase of strata bending moment. In Fig. 7(b), the azimuth force of BHA is decreased as the bending moment of strata is increased. In addition, the deviation force and azimuth force of BHA are obviously affected by direction and value of the bending moment of strata. The positive and negative of bending moment represent the anticlockwise and clockwise bending moment, respectively. Define $M_0=$ 0 as the dividing line, when $M_0$ is positive, the deviation force and azimuth force of BHA are decreased with the increase of $M_0$; however, when $M_0$ is negative, the deviation force and azimuth force of BHA are increased as $M_0$ increased. Therefore, the side force of BHA is sensitive to the bending moment of strata, in other words, strong heterogeneity of the gravel strata should lead to well deviation and drifting.

4.2. Deviating force of strata

According to Eqs. (20-25), deviating force of strata can be determined by the geologic parameters, such as dip angle of strata ($\beta$), comprehensive cutting anisotropy index ($H$) and angle of well inclination ($\alpha$). Therefore, the deviating force of strata is discussed according to the actual geological information shown in Fig. 8. The profiles of strata in north-south and east-west directions are depicted in Fig. 8(a) and (b), respectively. In Fig. 8(a), the dip angle of strata is described, and from the field data, the range of dip angle of strata is 7° to 13°. Besides, some basic parameters of geology are listed in Table 2. The comprehensive cutting anisotropy index can be determined by the state of equilibrium of BHA. When the angle of well inclination is unchanged or no more than 0.5°, the formula for calculating comprehensive cutting anisotropy index is expressed as:

26

$H=\frac{P_{\alpha }\left[1+\mathrm{t}\mathrm{a}{\mathrm{n}}^2\left(\beta -\alpha \text{'}\right)\right]}{P_{\alpha }+{P\text{'}}_B\mathrm{t}\mathrm{a}\mathrm{n}\left(\beta -\alpha \text{'}\right)\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\Delta }\varphi \text{'}}.$

By the analysis and calculation above, the maximum of $H$ is approached to 0.5 in air drilling.

Fig. 8The profile of gravel strata in the experiment well

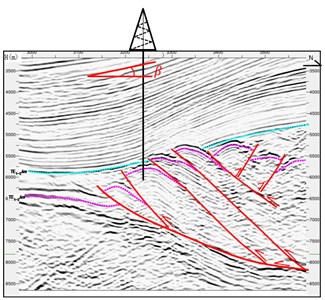
a) North-south

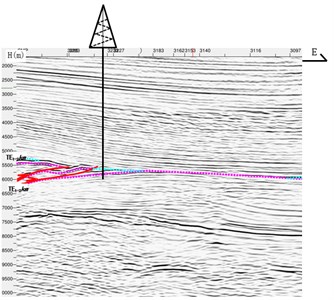
b) East-west

Table 2Parameter values of geology

No.	Parameters	Unit	Value
1	Dip angle of strata ($\beta$)	(°)	7-13
2	Azimuth difference ($\mathrm{\Delta }\varphi$)	(°)	40
3	Well inclination angle ($\alpha$)	(°)	0-5
4	Comprehensive cutting anisotropy index ($H$)		0.2-0.5

4.2.1. The effect of comprehensive cutting anisotropy index

The comprehensive cutting anisotropy index is determined by angle of well inclination, dip angle of strata, anisotropy of rock and anisotropic cutting property of the bit. Thus, the comprehensive cutting anisotropy index in the gravel stratum is complex during the drilling process. According to the characteristics of strata and the bit type, the value of comprehensive cutting anisotropy index $H$ ranges from 0.2 to 0.5 in air drilling. In this part, when $\beta =$ 10°, $\mathrm{\Delta }\varphi =$ 40° and $P_B=$ 20 kN, the deviating force of strata influenced by parameter $H$ is shown in Fig. 9. It is clearly indicated that the deviation and azimuth forces of gravel strata are significantly affected by the comprehensive cutting anisotropy index $H$, and the deviation and azimuth forces of strata are increased with the rising of $H$. Meanwhile, the bigger value of $H$ is, the faster deviating force of strata changes. Besides, when the angle of well inclination is smaller, the effect of $H$ on deviating force of strata is more sensitive. The symbol of azimuth force represents the drift direction of azimuth; when azimuth force is negative, the azimuth is drifted to the left; however, when azimuth force is positive, the azimuth is drifted to the right.

Fig. 9Influence of H on deviating force of strata

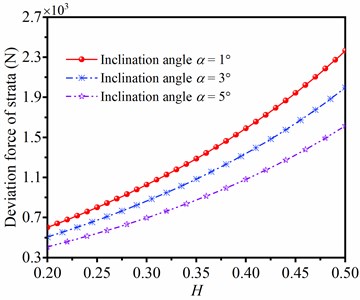
a) Deviation force of strata

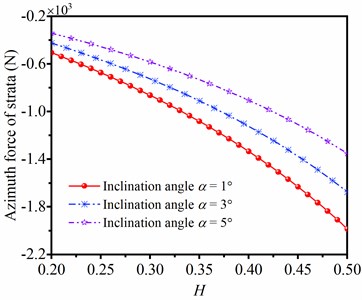
b) Azimuth force of strata

4.2.2. The effect of WOB

The angle of well inclination is unfixed in practical drilling process. Moreover, according to theoretical research, the angle of well inclination and WOB have great influence on strata deviating force. The deviation force and azimuth force of strata in different value of parameter $\alpha$ and WOB are discussed in Fig. 10. When angle of well inclination is unchanged, values of deviation force and azimuth force are increased with the rising of WOB; When WOB is unaltered, values of deviation force and azimuth force are decreased with the angle of well inclination. Therefore, large WOB in the bit leads to the improvement of deviating force of strata. In this case, when suffering from serious well deviation, low WOB is in favor of the decrease of well deviation; and low WOB is beneficial to reduce the left drift of well trajectory in the drilling process.

Fig. 10Influence of WOB on deviating force of strata

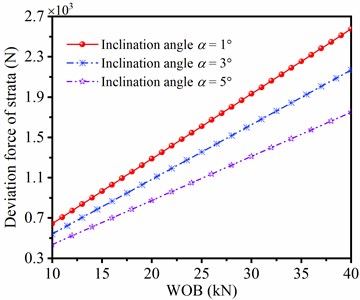
a) Deviation force of strata

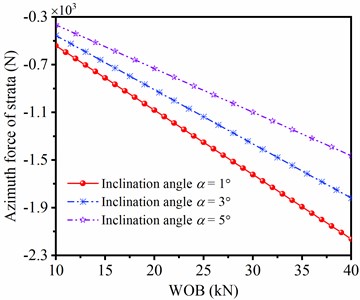
b) Azimuth force of strata

4.2.3. The effect of dip angle of strata

According to theoretical analysis, the dip angle of strata is a significant factor affecting on the deviating force of strata, thus it is necessary to investigate the influence of dip angle $\beta$ on deviating force of strata. The deviation and azimuth forces of strata with different dip angles of strata are shown in Fig. 11. In the same of inclination angle, the deviation force and azimuth force of strata are increased with the rising of dip angle. In addition, the lines of deviation force and azimuth force under different angles of well inclination are mutually paralleled with the increase of dip angle of strata, respectively. Therefore, the bigger dip angle of strata is, the larger deviation force of strata is, and the larger azimuth force of strata is.

Fig. 11Deviating force of strata in different dip angle of strata

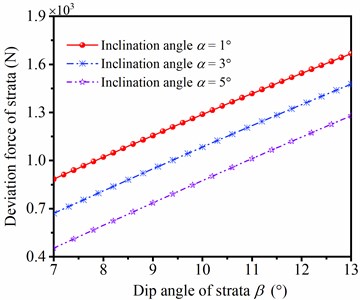
a) Deviation force of strata

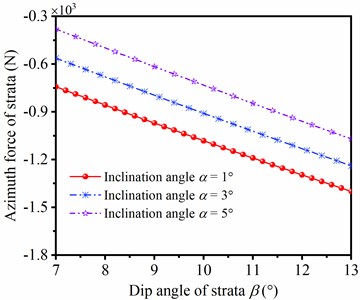
b) Azimuth force of strata

5. Experimental verification

To further demonstrate the reliability of theoretical analysis and numerical computation, a well in gravel strata with air drilling is adopted when the well depth is drilled in 3000-4500 m, and the type of BHA is in agreement with the section 4 in the actual drilling. Besides, inclination and azimuth angle of the well are shown in Fig. 12, and it is obviously seen that the inflection points of inclination and azimuth angle of the well are in vicinity of depth 4250 m as the minimum WOB is applied. In the upward inflection point, the inclination angle and azimuth angle is overall increased and decreased with the rising of well depth, respectively. However, in the downward inflection point, the inclination angle and azimuth angle is decreased and increased as the well depth is increased, respectively.

Fig. 12Measured inclination and azimuth angle in different well depth

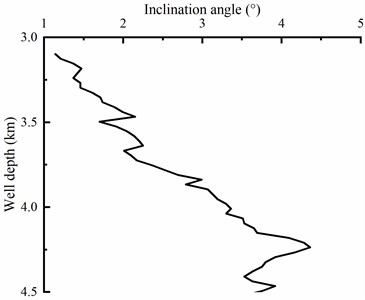
a) Inclination angle

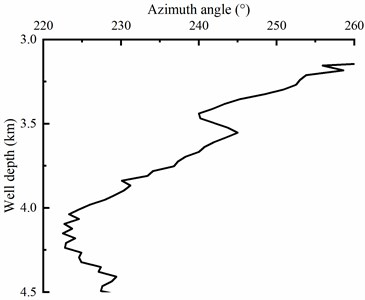
b) Azimuth angle

The side force of BHA and deviating force of strata in different well depth are listed in Table 3. Moreover, the superposition of side force of BHA and deviating force of strata is given in Table 4. It can be seen that the superposition of deviation force between BHA and strata is positive, in this case, the inclination angle is increased in theoretical computation, which is agreement with the measured inclination angle. In addition, the superposition of azimuth force between BHA and strata is negative, in this case, the azimuth is left drifted in theoretical computation, which is consistent with the measured azimuth angle. Therefore, according to the results of theoretical analysis, numerical computation and field measurement, it can be found that the mechanical model of BHA and deviating force model of gravel strata in this paper can predict the borehole trajectory in air drilling engineering.

6. Conclusions

In this paper, the well deviation in air drilling is analyzed from statics of BHA and deviating force of strata through theoretical study, numerical simulation and experimental verification. Some conclusions are listed as follow:

1) The side force of BHA is sensitive to ERBD, angle of well inclination, bending moment of strata in air drilling, but insensitive to WOB. Besides, the large outer diameter of drill collar is beneficial to decrease the well deviation, but exacerbates the azimuth drift of well trajectory.

2) The maximum of comprehensive cutting anisotropy index $H$ is approached to 0.5 in air drilling. It is clearly indicated that the deviation and azimuth forces of gravel strata are significantly affected by $H$, and the deviation and azimuth forces of strata are increased with the rising of $H$. Meanwhile, large WOB in the BHA leads to the improvement of deviating force of strata. In this case, when suffering from serious well deviation, low WOB is in favor of the decrease of well deviation; and low WOB is beneficial to reduce the left drift of well trajectory. In addition, the bigger dip angle of strata, the larger deviation force of strata, and the larger azimuth force of strata.

3) According to the results of theoretical analysis, numerical computation and field measurement, it can be seen that the mechanical models of BHA and gravel strata in this paper can accurately predict the borehole trajectory in air drilling.