Abstract
Carbon fiber reinforced polymer is a composite material, which is widely used in various engineering fields due to its excellent properties. We systematically discuss the influence of axial load amplitude parameters on the multiple periodic motions of carbon fiber reinforced polymer laminated cylindrical shell model. Based on the Melnikov vector function, the bifurcation regions of periodic orbits are obtained. It is found that the system has at most four periodic orbits under parameters conditions. Moreover, the phase portraits of periodic orbits are given by numerical simulation. The results offer an idea for parameter control of shell structure.
1. Introduction
Compared with conventional materials, carbon fiber reinforced polymer shows better heat resistance and corrosion resistance. It is a kind of lightweight and high strength engineering structural composite material, which has a positive impact on the development of aerospace, medical devices, rail transportation and other fields [1-4]. Therefore, in order to fully exploit the advantages of novel composite materials and maximize their role as structures in practical engineering applications, it is essential to study the dynamic characteristics of novel composite plate and shell structures.
A large number of scholars have studied carbon fiber composite materials and cylindrical shell structure. Under the internal resonance condition, Zhang et al. [5] discussed the response characteristic and complex dynamic behaviors of cylindrical shell model. Poul et al. [6] analyzed the enhancement effect of the plastic layer of carbon fiber reinforced thin steel sheet under shear load through experimental research. Lim [7] studied the natural frequencies of different plate and shell structures under free and simply supported boundary conditions with negative Poisson's ratio. Zhang et al. [8] devoted to study the influences of radial linear load and axial load at both ends of the carbon fiber reinforced composite laminated cylindrical shell on the nonlinear radial breathing vibration.
The literature review showed that there are many researches on mechanical property and nonlinear vibration behaviors of shell structures. However, little attention has been paid to the periodic or multiple periodic vibration behaviors of cylindrical shells structure. The development of periodic solutions theory [9-11] is conducive to a deep understanding of the vibration characteristics of the system in different parameter regions, and provides guidance for the vibration reduction design of nonlinear dynamics theory.
Motivated by this, we pay attention to the multiple periodic motions and its parameter control conditions of the carbon fiber reinforced polymer laminated cylindrical shell structure. In Section 2, original coupled system and averaged equation are given. In Section 3, the multiple periodic motions are studied by Poincaré map and the Melnikov function, and the bifurcation parameter is obtained. The number of periodic solutions in different parameter areas is 0, 2, 4 respectively. In Section 4, the phase configurations of periodic orbits are presented by MATLAB software. In Section 5, we give the conclusions.
2. Dynamic model and averaged equation
2.1. Dynamic model
We focus on the carbon fiber reinforced polymer laminated cylindrical shell structure subjected to different loads, which can be modeled by the two degrees-of-freedom governing equation [8]:
where, . , represent the vibration amplitude of the first and second order modesrespectively. represent damping coefficients. are two linear natural frequencies. are radial line load amplitude. is axial load amplitude. are frequency under external excitation. , represent the dimensionless coefficient.
2.2. Averaged equation
The system given in the above section is a four-dimensional non-autonomous system. We need to analyze the perturbation of Eq. (1). Considering the following internal resonance relationship:
where , are the detuning parameters.
We assume that . The following scale transformations are introduced as:
For the convenience of calculation, we use the multiple scales method to obtain the averaged equation of the system with the help of MAPLE software:
where , is a vector-valued polynomial in variables of . . . . The symbol represents a block matrix with -th blockand all other blocks are zero matrices [12].
Introducing the transformation , system Eq. (4) can be rewritten as:
where , , , . In addition, , . Therefore, the study of multiple periodic motions of original system Eq. (1) can be transformed into the study of bifurcation of multiple periodic solutions of the system Eq. (5).
2.3. Periodic motions
When , system Eq. (5) degenerates to two uncoupled Hamiltoniansystems on plane and . Then each system has a family of periodic orbits: , surrounding the origin of the system for . Assuming that can be expressed as:
We introduce the curvilinear coordinates in the neighborhood of the invariant torus . Define a global cross section in the phase space, and construct theth iteration of Poincaré map . We need to calculate the simple zero of the Melnikov function , where:
Let , then we can obtain:
where , , ,
Our goal is to analyze the number of solutions for of Eqs. (6-8), so we let . Assuming that , , from Eqs. (6-7), we can obtain:
where , . Substituting Eq. (9) into Eq. (8), we have:
where , , . When and , the system has four periodic solutions.
3. Numerical simulation
We detect the existence and multiplicity of periodic vibrations by changing the value of. The parameters conditions are as follows:
(1) The axial load amplitude ( is the critical parameter value). In this case, the system Eq. (1) is only subjected to the radial line load, and . There is a pair of periodic orbit: . Fig. 1 represents the phase configurations of the periodic orbits projected on various planes and spaces.
Fig. 1There are two periodic orbits when p1=0
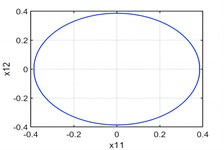
a) plane
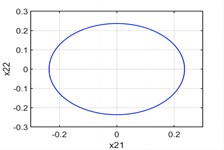
b) plane
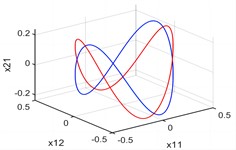
c) space
(2) The axial load amplitude . In this case, there are four periodic solutions. Figs. 2-3 represent the phase portraits of the periodic orbits projected on various planes and spaces when , . When , the four periodic orbits can be divided into two pairs:
When , the four periodic orbits can be divided into two pairs:
When is increased to , the distance between two pairs of periodic orbits becomes closer and closer. The periodic orbit with larger amplitude and the periodic orbit with smaller amplitude are gradually increasing, and the former increases slower than the latter. It should be noted that we have tried multiple sets of different values of to confirm whether the periodic motions continue in this manner. Only two sets of data are listed here.
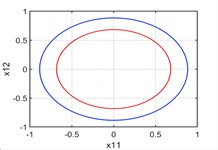
Fig. 2There are four periodic orbits when p1=1.5
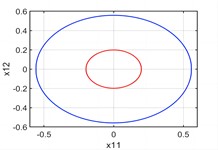
a) plane
b) plane
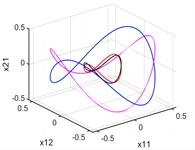
c) space
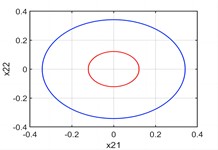
Fig. 3There are four periodic orbits when p1=3.5
a) plane
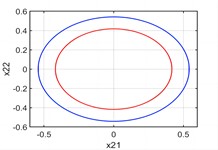
b) plane
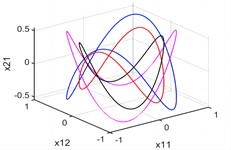
c) space
(3) The axial load amplitude . In this case, the system has two periodic solutions satisfying . The periodic vibration phase diagrams of the system are shown in Fig. 4. We can observe that the periodic orbits and coincide into when .
Fig. 4There are two periodic orbits when p1=p10
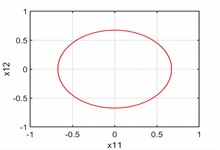
a) plane
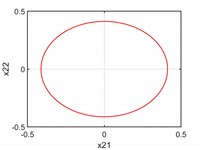
b) plane
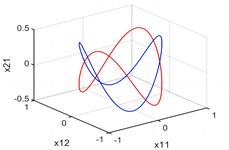
c) space
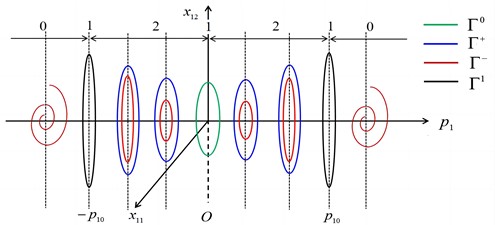
When , we have analyzed the specific bifurcation phenomenon when passes through from left to right. This change also occurs when passes through . As shown in Fig. 5, we use space to describe the whole process. We can clearly see that when crosses from left to right, the periodic trajectory splits immediately, forming two pairs of periodic trajectories. With the increase of , the increase rate of the amplitude of is less than that in , that is, gradually approaching. The periodic orbits and coincide at to form , and then disappear when . Above, we only analyze the effect of the axial load amplitude on the number of periodic orbits and the form of spiral. When . The analysis of is similar to it.
Fig. 5Bifurcation of periodic orbits in (x11,x12,p1) space
4. Conclusions
It is essential to study periodic motions of cylindrical shell structure which is closely intertwined with energy transfer and vibration analysis. In this paper, the Melnikov function is obtained, which is different from the traditional quantitative method. Under certain parameter conditions, it is clear from theoretical and numerical results that the system has multiple periodic motions. We take the axial load amplitude as bifurcation parameter to study the evolution law of the periodic orbits, and obtain the detailed bifurcation diagram about the parameter of , as shown in Fig. 5. It is found that the periodic motion of cylindrical shells structure is more sensitive to axial load than radial line load, which is consistent with the results obtained in Ref. [8], and further illustrates the correctness of the theoretical analysis in this paper.
References
-
S. Qu et al., “Underwater metamaterial absorber with impedance-matched composite,” Science Advances, Vol. 8, No. 20, May 2022, https://doi.org/10.1126/sciadv.abm4206
-
T. Xu, S. Zhang, J. Liu, X. Wang, and Y. Guo, “Seismic behavior of carbon fiber reinforced polymer confined concrete filled thin-walled steel tube column-foundation connection,” Composite Structures, Vol. 279, p. 114804, Jan. 2022, https://doi.org/10.1016/j.compstruct.2021.114804
-
M. Yang, J. Xie, S. Kainuma, and W. Liu, “Improvement in bond behavior and thermal properties of carbon fiber-reinforced polymer strengthened steel structures,” Composite Structures, Vol. 278, p. 114704, Dec. 2021, https://doi.org/10.1016/j.compstruct.2021.114704
-
Z. Zhang, D. Yavas, Q. Liu, and D. Wu, “Effect of build orientation and raster pattern on the fracture behavior of carbon fiber reinforced polymer composites fabricated by additive manufacturing,” Additive Manufacturing, Vol. 47, p. 102204, Nov. 2021, https://doi.org/10.1016/j.addma.2021.102204
-
W. Zhang, T. Liu, A. Xi, and Y. N. Wang, “Resonant responses and chaotic dynamics of composite laminated circular cylindrical shell with membranes,” Journal of Sound and Vibration, Vol. 423, pp. 65–99, Jun. 2018, https://doi.org/10.1016/j.jsv.2018.02.049
-
M. Khazaei Poul, F. Nateghi-Alahi, and X. L. Zhao, “Experimental testing on CFRP strengthened thin steel plates under shear loading,” Thin-Walled Structures, Vol. 109, pp. 217–226, Dec. 2016, https://doi.org/10.1016/j.tws.2016.09.026
-
T. C. Lim, Auxetic Materials and Structures. Singapore: Springer, 2015.
-
W. Zhang, S. W. Yang, and J. J. Mao, “Nonlinear radial breathing vibrations of CFRP laminated cylindrical shell with non-normal boundary conditions subjected to axial pressure and radial line load at two ends,” Composite Structures, Vol. 190, pp. 52–78, Apr. 2018, https://doi.org/10.1016/j.compstruct.2018.01.091
-
J. Li, Z. Guo, S. Zhu, and T. Gao, “Bifurcation of periodic orbits and its application for high-dimensional piecewise smooth near integrable systems with two switching manifolds,” Communications in Nonlinear Science and Numerical Simulation, Vol. 116, p. 106840, Jan. 2023, https://doi.org/10.1016/j.cnsns.2022.106840
-
J. Llibre and T. Salhi, “On the limit cycles of the piecewise differential systems formed by a linear focus or center and a quadratic weak focus or center,” Chaos, Solitons and Fractals, Vol. 160, p. 112256, Jul. 2022, https://doi.org/10.1016/j.chaos.2022.112256
-
X. Guo, R. Tian, Q. Xue, and X. Zhang, “Sub-harmonic Melnikov function for a high-dimensional non-smooth coupled system,” Chaos, Solitons and Fractals, Vol. 164, p. 112629, Nov. 2022, https://doi.org/10.1016/j.chaos.2022.112629
-
J. Li, L. Zhang, and D. Wang, “Unique normal form of a class of 3 dimensional vector fields with symmetries,” Journal of Differential Equations, Vol. 257, No. 7, pp. 2341–2359, Oct. 2014, https://doi.org/10.1016/j.jde.2014.05.039
About this article
This research was supported by National Natural Science Foundation of China (Grant No.12272011) and also supported by National Key R&D Program of China (Grant No. 2022YFB3806000).
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
