Abstract
Sloshing in coaxial shells partially filled with liquid is investigated using reduced boundary element method. Conical shells are considered as storage tanks. An ideal and incompressible fluid is assumed in the shells. The spectral boundary problem for the liquid vibrations in rigid shells is solved. The results demonstrate the high accuracy of the presented approach.
1. Introduction
The term “sloshing in tanks” describes a phenomenon in which the movement of the liquid inside a tank causes oscillations because of outside forces operating on the tank. This can happen in a variety of tanks, such as water or fuel tanks, or even cargo tanks inside space vessels or ships. Shells and structures resembling shells are prevalent components in contemporary mechanical engineering. These structures are frequently employed as fuel tanks for launch vehicles, reservoirs for storing fresh water, and other substances, including potentially hazardous explosives. When these tanks are subjected to substantial loads, there is a risk of intensive liquid sloshing, resulting in highly perilous consequences. It's important to highlight that the development of each new launch vehicle necessitates the design of novel fuel tanks.
A variety of tank designs are considered to discuss sloshing [1], [2]. Most common methods to discuss sloshing are BEM [3], FEM [4], FVM [5], and series expansions [6]. Many studies on modal analysis and frequencies have been reported in previous studies such as [2], [7], and [8]. Studies [9], [10] and [11] are devoted to developing analytical methods to analyze sloshing. Studies involving the theoretical and experimental aspects of the stability of tanks are reported in [12], [13] and [19].
The design and manufacture of new powerful launch vehicles necessitate the development of new fuel tanks. Currently, such tanks increasingly take the form of compound shells. To mitigate undesirable resonant frequencies, it is necessary to study the entire frequency spectrum of the tank's inherent vibrations, specifically under various fuel fill levels and different levels of loading. It is necessary to estimate the natural frequencies of empty tanks, the frequencies of elastic wall oscillations in the presence of liquid, as well as the sloshing frequencies. However, the investigation of vibrations of compound shells with compartments partially filled with liquid has not received sufficient attention in the literature [14]. Therefore, the study of vibrations of compound coaxial cylindrical and cylindrical-conical shells with liquid is a relevant scientific task.
2. Methodology
BEM is computationally efficient compared to other methods like the finite element method (FEM) or finite difference method (FDM), it can still be resource-intensive for large-scale engineering problems. To further reduce the computational cost of the boundary element method, several techniques and variations have been developed. One such technique is the “reduced” boundary element method, which aims to reduce the dimensionality of the problem or to simplify the computation further.
The main objective of this research lies in developing an efficient numerical method based on reduced boundary element (BEM) method to assess the sloshing frequencies of vibrations in compound liquid-filled reservoirs.
3. Problem statement
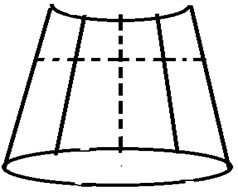
The geometry of the problem is shown in Fig. 1. and denote the free surface of the liquid and wetted surface of the shell respectively. An ideal and incompressible fluid is assumed to perform the motion inside the shells.
Fig. 1Сylindrical – conical compound shells
The following boundary value problem is formulated as follows:
Here the unknown function characterizes the variations in position and shape of the free surface over time. So, it is necessary to determine the unknown functions and .
The unknown functions and in cylindrical coordinates are expressed as:
Here time-dependent coefficients are unknown. From Eq. (1), the basic functions and are solutions to such a linear spectral boundary value problem:
where are fundamental frequencies. As it has been shown in [3], for shells of revolution, all unknown functions for each wave number can be expressed in the following form:
Such presentation simplifies the analysis by reducing the problem to a series of uncoupled single-degree-of-freedom systems, depending on , making the numerical estimations computationally more efficient. Moreover, for the shells of revolution, reduced finite and boundary element methods can be applied.
4. Results and discussion
4.1. Validation
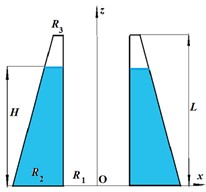
For validation study, the numerical results obtained by proposed BEM have been compared with data of [18]. The numerical simulation focuses on frequencies for 0, 1, 2 and 1, as these are the lowest natural frequencies contributing significantly to the hydrodynamic load. Both V-shape and -shape conical tanks are considered in the simulation, with 1 m and /6.
Note, that for a V-shape tank, is the free surface radius, while for a -shape tank, is the bottom radius. If , , and are known, the value of can be found as . Table 1 presents the numerical results for 0, 1, 2, and different values of .
Table 1Sloshing frequencies in conical shells
V-shape | -shape | |||||||||
0.2 | 0.4 | 0.6 | 0.8 | 0.9 | 0.2 | 0.4 | 0.6 | 0.8 | 0.9 | |
0, 1 | ||||||||||
[18] | 3.386 | 3.386 | 3.382 | 3.139 | 2.187 | 24.153 | 10.014 | 6.665 | 4.550 | 2.683 |
BEM | 3.389 | 3.390 | 3.391 | 3.192 | 2.200 | 20.027 | 10.034 | 6.669 | 4.545 | 2.678 |
1, 1 | ||||||||||
[18] | 1.304 | 1.302 | 1.254 | 0.934 | 0.542 | 11.332 | 5.629 | 3.515 | 1.661 | 0.726 |
BEM | 1.305 | 1.307 | 1.259 | 0.954 | 0.574 | 11.303 | 5.626 | 3.481 | 1.651 | 0.732 |
The comparison of results obtained by the proposed method with the data of [18] shows good agreement, except for the data related to the Ʌ-shape tank at 0 and 0.2 m. It is noted in [18] that in this particular case, low convergence was achieved using the elaborated analytical method.
4.2. Sloshing in cylindrical-conical shells
The solution of spectral boundary value problem Eq. (3) made it possible to find the modes and corresponding fundamental frequencies. The values of the first 8 sloshing frequencies are given in Table 2.
Table 2Sloshing frequencies, Hz
No | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Shell structure, Fig. 1(a) | ||||||||
Values | 0.6277 | 0.6277 | 0.8892 | 0.8892 | 1.0779 | 1.0779 | 1.2355 | 1.2355 |
Shell structure, Fig. 1(b) | ||||||||
Values | 0.5512 | 0.5512 | 0.8153 | 0.8153 | 1.0027 | 1.0027 | 1.1548 | 1.1548 |
It should be noted that the multiple frequencies are available. The sloshing modes are presented in Fig. 2.
The lowest frequencies correspond to 1st, 2nd and 3rd wave numbers, which is consistent with the data [5].
5. Conclusions
The reduced boundary element method for sloshing analysis in coaxial shells shell structures partially filled with liquid is used to calculate frequencies. The spectral boundary problem for the liquid vibrations in rigid shells is solved. The mode shapes are reported for the considered problem. The further intention is to consider forced vibrations at different levels of gravity [6].
Fig. 2Sloshing modes φkr,θ, H
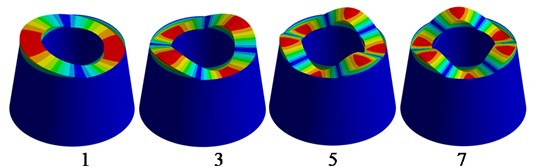
a) Sloshing modes of shell structure Fig. 1(a)
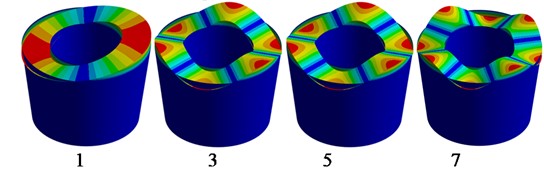
b) Sloshing modes of shell structure Fig. 1(b)
References
-
V. S. Hudramovich, V. N. Sirenko, D. V. Klimenko, Y. F. Daniev, and E. L. Hart, “Development of the normative framework methodology for justifying the residual resource of starting buildings’ constructions of space launch vehicles,” Strength of Materials, Vol. 51, No. 3, pp. 333–340, Aug. 2019, https://doi.org/10.1007/s11223-019-00079-4
-
A. Karaiev and E. Strelnikova, “Liquid sloshing in circular toroidal and coaxial cylindrical shells,” in Lecture Notes in Mechanical Engineering, Springer, 2020, https://doi.org/10.1007/978-3-030-50491-
-
V. I. Gnitko, K. G. Degtyariov, A. O. Karaiev, and E. A. Strelnikova, “Singular boundary method in a free vibration analysis of compound liquid-filled shells,” BEM/MRM 42 2019, Vol. 126, pp. 189–200, Sep. 2019, https://doi.org/10.2495/be420171
-
S. Misura, N. Smetankina, and I. Misiura, “Optimal design of the cyclically symmetrical structure under static load,” in Lecture Notes in Networks and Systems, pp. 256–266, Jan. 2021, https://doi.org/10.1007/978-3-030-66717-7_21
-
P. Lampart, A. Rusanov, S. Yershov, S. Marcinkowski, and A. Gardzilewicz, “Validation of a 3D BANS solver with a state equation of thermally perfect and calorically imperfect gas on a multi-stage low-pressure steam turbine flow,” Journal of Fluids Engineering, Transactions of the ASME, Vol. 127, No. 1, pp. 83–93, 2005, https://doi.org/10.1115/1.185249
-
N. Smetankina, A. Pak, O. Mandrazhy, O. Usatova, and A. Vasiliev, “Modelling of free axisymmetric vibrations of the fluid-filled shells with non-classical boundary interface conditions,” in Smart Technologies in Urban Engineering, pp. 185–196, Dec. 2023, https://doi.org/10.1007/978-3-031-46874-2_17
-
N. Kumar and N. Choudhary, “Sloshing reduction in three-dimensional rectangular container using rigid baffles,” Vibroengineering Procedia, Vol. 42, pp. 39–44, May 2022, https://doi.org/10.21595/vp.2022.22550
-
N. Kumar and N. Choudhary, “Simulation and semi-analytical approach on sloshing mitigation,” in 2021 International Conference on Recent Advances in Mathematics and Informatics (ICRAMI), pp. 1–4, Sep. 2021, https://doi.org/10.1109/icrami52622.2021.9585926
-
N. Choudhary, S. N. Bora, and E. Strelnikova, “Study on liquid sloshing in an annular rigid circular cylindrical tank with damping device placed in liquid domain,” Journal of Vibration Engineering and Technologies, Vol. 9, No. 7, pp. 1577–1589, Jun. 2021, https://doi.org/10.1007/s42417-021-00314-w
-
E. A. Strelnikova, N. Choudhary, D. V. Kriutchenko, V. I. Gnitko, and A. M. Tonkonozhenko, “Liquid vibrations in circular cylindrical tanks with and without baffles under horizontal and vertical excitations,” Engineering Analysis with Boundary Elements, Vol. 120, pp. 13–27, Nov. 2020, https://doi.org/10.1016/j.enganabound.2020.07.024
-
O.-M. Balaş, C. V. Doicin, and E. C. Cipu, “Analytical and numerical model of sloshing in a rectangular tank subjected to a braking,” Mathematics, Vol. 11, No. 4, p. 949, Feb. 2023, https://doi.org/10.3390/math11040949
-
J. Liu, Q. Zang, W. Ye, and G. Lin, “High performence of sloshing problem in cylindrical tank with various barrels by isogeometric boundary element method,” Engineering Analysis with Boundary Elements, Vol. 114, pp. 148–165, May 2020, https://doi.org/10.1016/j.enganabound.2020.02.014
-
V. Gnitko, K. Degtyarev, V. Naumenko, and E. Strelnikova., “Coupled BEM and FEM analysis of fluid-structure interaction in dual compartment tanks,” International Journal of Computational Methods and Experimental Measurements, Vol. 6, No. 6, pp. 976–988, 2018, https://doi.org/10.2495/cmem-v6-n6-976-
-
Z. Zhang, A.-F. Tao, Q.-R. Wu, and Y.-H. Xie, “Review on the progress and issues in liquid tank sloshing of ships,” China Ocean Engineering, Vol. 37, No. 5, pp. 709–724, Nov. 2023, https://doi.org/10.1007/s13344-023-0060-0
-
A. Karaiev and E. Strelnikova, “Axisymmetric polyharmonic spline approximation in the dual reciprocity method,” ZAMM – Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 101, No. 4, Jan. 2021, https://doi.org/10.1002/zamm.201800339
-
C. A. Brebbia, J. C. F. Telles, and L. C. Wrobel, Boundary Element Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1984, https://doi.org/10.1007/978-3-642-48860-3
-
A. Karaiev and E. Strelnikova, “Singular integrals in axisymmetric problems of elastostatics,” International Journal of Modeling, Simulation, and Scientific Computing, Vol. 11, No. 1, p. 2050003, Feb. 2020, https://doi.org/10.1142/s1793962320500038
-
I. Gavrilyuk, M. Hermann, I. Lukovsky, O. Solodun, and A. Timokha, “Natural sloshing frequencies in rigid truncated conical tanks,” Engineering Computations, Vol. 25, No. 6, pp. 518–540, Aug. 2008, https://doi.org/10.1108/02644400810891535
-
N. Choudhary and E. Strelnikova, “Liquid vibrations in a container with a membrane at the free surface,” Vibroengineering Procedia, Vol. 37, pp. 13–18, May 2021, https://doi.org/10.21595/vp.2021.21996
About this article
The authors gratefully acknowledge the support from their institutions.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
