A Comprehensive examination of utilizing neutrosophic parameters in manufacturing industry through queueing approach

1. Introduction

The incorporation of Neutrosophic parameters into $M/G/1$ queueing systems presents a groundbreaking strategy for tackling uncertainties prevalent in real-world scenarios. This paper conducts a thorough examination of this integration, elucidating the core tenets of both queueing theory and Neutrosophic set theory. It explores methodologies for integrating Neutrosophic parameters and evaluates their impact on crucial performance metrics, showcasing the potential of this approach to enhance the accuracy and resilience of queueing models. By bridging these theoretical frameworks, this study contributes to a deeper comprehension of system dynamics in uncertain environments, offering valuable insights for optimization. As a well-established field of mathematical statistics, queuing theory has made a significant contribution to the efficiency and optimization of many different systems, especially in operations and manufacturing. Conventional queueing models might not fully meet the issues posed by the dynamic and complicated character of current production processes. This is where Neutrosophic Parameter integration can be highly beneficial.

Neutrosophic Parameters are required in queueing techniques to manage inconsistent and uncertain data, which is common in actual production settings. Through more precise forecasts and efficient resource allocation, this integration improves decision-making. It also speeds up system performance by cutting down on wait times and makes production systems more resilient to interruptions. In the end, Neutrosophic Queueing Models provide a stronger and more adaptable framework, which makes them ideal for optimizing modern manufacturing processes.

In order to provide a more precise and adaptable framework for actual industrial settings, this study investigates the new integration of Neutrosophic Parameters into queueing models. This integration goes beyond fuzzy logic to encompass indeterminate and inconsistent information. This study is novel because it can better handle the dynamic nature of manufacturing processes, make better decisions, and increase system performance by cutting down on inefficiencies. This work provides a revolutionary breakthrough in manufacturing process optimization by utilizing Neutrosophic Parameters, increasing the applicability and efficacy of queueing models in the complex and uncertain manufacturing environment of today.

Alhabib, Ranna, Farah, and Salama [1] explored various probability distributions using neutrosophic analysis. Buckley [2] analyzed Elementary queueing theory based on possibility theory. while Cochran, Cox, Keskinocak, Kharoufeh, Smith, and Boxma [3] examined the $M/G/1$ Queue under various conditions. Kalpana and Anusheela [4] examined a single server non-preemptive fuzzy priority queue using the LR Method. Masri, Fatina, Zeina, and Omar Zeitouny [5] introduced Maple Code-based single-valued neoclassic queuing systems, Miller [6] scrutinized the $M/M/1$ priority queue under steady-state probabilities, while Pardo, de la Fuente [7] utilized fuzzy set theory to optimize and analyze a priority-discipline queueing model. Rashad, Heba, and Mai Mohamed [8] elaborated on neutronomic theory and its application in various queuing models. Salama and Smarandache [9] investigated decision-making and neutrosophic crisp probability theory. The foundational aspects of queuing theory were discussed by Shortle, Thompson, Gross, and Harris. Buckley [10] delved into the realm of possibility-based elementary queueing theory, Smarandache [11] contributed to the integration of neutrosophic theory into logic, probability, and sets, Suvitha, Broumi, and Mohanaselvi [12] investigated the Neutrosophic queuing model under priority discipline. Tomov, Krawczak, Andonov, Atanassov, and Simeonov [13] developed generalized net models for queueing disciplines in finite buffer systems with intuitionistic fuzzy task evaluations. Yasodai and Ritha [14] utilized parametric programming techniques to examine the Neutrosophic Fuzzy Erlangian Queuing Model. while Zeina [15] discussed the Neutrosophic M/M/1 Linguistic Single Valued Queue. Zeina, Khudr Al-Kridi, and Mohammed Taher Anan [16] introduced a novel method for performance measure analysis in the $FM/FM/1$ Queue. Additionally, Zeina [17] investigated $M/M/1/b$, $M/M/c$, and Neutrosophic $M/M/1$ queuing systems. Zeina [18] analyzed the Erlang Service Queueing Model using neutrosophic parameters and developed the Neutrosophic Event-Based Queueing Model [19].

Embarking on uncharted territory, this study pioneers the exploration of $M/G/1$ queues within neutrosophic frameworks, expanding the horizons of queueing theory. Navigating uncertainties, we apply neutrosophic philosophy to analyze performance measures across distributions like exponential, Erlang, and deterministic in-service times. Through numerical illustrations, we compare the outcomes of neutrosophic queues with crisp ones, unveiling novel insights.

2. M/G/1 queueing models [3, 18]

The $M/G/1$ queue depicts a scenario in queueing theory where a single server manages a queue characterized by Poisson arrival processes and general service time distributions. This model is foundational in various domains such as telecommunications, computer systems, and customer service operations. Unlike simpler models, $M/G/1$ accounts for variability in service times, offering a more realistic representation of real-world scenarios. Analyzing $M/G/1$ queues provide insights into system performance metrics like average waiting time, queue length, and server utilization. These insights aid in optimizing resource allocation, system design, and operational strategies to enhance efficiency and meet performance objectives amidst stochastic environments.

The performance measures can be calculated using the mean arrival rate $\lambda$, mean service rate $\mu$ and the utilization factor $\rho .$

Performance measures of $M/G/1$ queueing models are:

Expected number of customers in the system:

Expected number of customers in the queue:

Expected waiting time of a customer in the system:

Expected waiting time of a customer in the queue:

The squared coefficient of variation ${C_M}^2={{\sigma }_M}^2{\mu }^2$, makes the Table 1.

The performance measures of $M/G/1$ can be synthesized into $M/M/1$ model when $C_M$ takes the value 1; $M/E_k/1$ model when $C_M$ takes the value$1/\sqrt{k}$; $M/D/1$ model when $C_M$ takes the value 0.

3. Numerical illustration: case study

Statement: The data center in Coimbatore, India functions as a central system, akin to a server, managing three diverse communication lines, encompassing Ethernet, Wi-Fi, and Bluetooth. Each line experiences an average message transmission time of 2.5 seconds and operates at 80 % bandwidth utilization. The data traffic distribution across these communication lines within a single system adheres to an exponential model for line 1, Erlang-3 model for line 2, and a deterministic model for line 3. Analyze how do different communication models (exponential, Erlang, deterministic) influence data traffic distribution and the overall performance of the system? Additionally, what are the comparative performance metrics among the three communication lines, enabling an assessment of their efficiency and reliability?

Solution:

By examining bandwidth utilization and message transmission time, we can assess system stability, quality of service, and overall performance. This data can be correlated with the $M/G/1$ queuing system, as the communication system employs three distinct models across its three lines.

Initially, we will compute the performance metrics for each line individually using crisp queue (Queueing theory concept) and neutrosophic queueing theory. Subsequently, we will compare the outcomes to forecast future system behavior and performance under various scenarios or conditions.

The message transmission time, i.e., service time $\mu =\text{1}/\text{2.5}$ seconds = 0.4 seconds.

Utilization factor $\rho =\text{0.8}$, from which we get the inter arrival time $\lambda =$0.32 seconds.

3.2. Neutrosophic queue

3.2.1. Case (i)

The line 1 follows neutrosophic exponential service time. The performance metrics can be evaluated by taking $C_M$ equal to $1$ in $NM/NG/1$ queue formula. In $NM/(NG\equiv NM)/1$ queue, the inter arrival time of the customer is specified by an Exponential distribution with mean arrival rate ${\lambda }_N=\left[{\lambda }_L,{\lambda }_U\right]=\left[\mathrm{0.31,0.33}\right]$. The service rate of the customer is specified by Poisson distribution ${\mu }_N=\left[{\mu }_L,{\mu }_U\right]=\left[\mathrm{0.39,0.41}\right]$ with the utilization factor ${\rho }_N={\lambda }_N/{\mu }_N=\left[\mathrm{0.79,0.81}\right].$

Performance measures of $NM/(NG\equiv NM)/1$ queueing models are:

1) Expected number of customers in the system:

29

${NL}_s=\left[\frac{{\lambda }_L}{{\mu }_U},\frac{{\lambda }_U}{{\mu }_L}\right]+\left(\frac{{{1+C}_M}^2}{2}\right)\left[\frac{{\left(\frac{{\lambda }_L}{{\mu }_U}\right)}^2}{\left(1-\frac{{\lambda }_L}{{\mu }_U}\right)},\frac{{\left(\frac{{\lambda }_U}{{\mu }_L}\right)}^2}{\left(1-\frac{{\lambda }_U}{{\mu }_L}\right)}\right],$

30

${NL}_S=\left[\frac{0.31}{0.41},\frac{0.33}{0.39}\right]+\left(\frac{{1+1}^2}{2}\right)\left[\frac{{\left(\frac{0.31}{0.41}\right)}^2}{\left(1-\frac{0.31}{0.41}\right)},\frac{{\left(\frac{0.33}{0.39}\right)}^2}{\left(1-\frac{0.33}{0.39}\right)}\right]=\left[\mathrm{3.17,5.67}\right].$

2) Expected number of customers in the queue:

31

${NL}_q=\left(\frac{{{1+C}_M}^2}{2}\right)\left[\frac{{\left(\frac{{\lambda }_L}{{\mu }_U}\right)}^2}{\left(1-\frac{{\lambda }_L}{{\mu }_U}\right)},\frac{{\left(\frac{{\lambda }_U}{{\mu }_L}\right)}^2}{\left(1-\frac{{\lambda }_U}{{\mu }_L}\right)}\right],$

32

${NL}_q=\left(\frac{{1+1}^2}{2}\right)\left[\frac{{\left(\frac{0.31}{0.41}\right)}^2}{\left(1-\frac{0.31}{0.41}\right)},\frac{{\left(\frac{0.33}{0.39}\right)}^2}{\left(1-\frac{0.33}{0.39}\right)}\right]=\left[\mathrm{2.41,4.82}\right].$

3) Expected waiting time of a customer in the system:

33

${NW}_s=\left[\frac{1}{{\mu }_U},\frac{1}{{\mu }_L}\right]+\left(\frac{{{1+C}_M}^2}{2}\right)\left[\frac{\frac{{\lambda }_L}{{\mu }_U}}{\left({\mu }_U-{\lambda }_L\right)},\frac{\frac{{\lambda }_U}{{\mu }_L}}{\left({\mu }_L-{\lambda }_U\right)}\right],$

34

${NW}_s=\left[\frac{1}{0.41},\frac{1}{0.39}\right]+\left(\frac{{1+1}^2}{2}\right)\left[\frac{\frac{0.31}{0.41}}{\left(0.41-0.31\right)},\frac{\frac{0.33}{0.39}}{\left(0.39-0.33\right)}\right]=\left[\mathrm{10.04,16.73}\right].$

4) Expected waiting time of a customer in the queue:

35

${NW}_q=\left(\frac{{{1+C}_M}^2}{2}\right)\left[\frac{\frac{{\lambda }_L}{{\mu }_U}}{\left({\mu }_U-{\lambda }_L\right)},\frac{\frac{{\lambda }_U}{{\mu }_L}}{\left({\mu }_L-{\lambda }_U\right)}\right],$

36

${NW}_q=\left(\frac{{1+1}^2}{2}\right)\left[\frac{\frac{0.31}{0.41}}{\left(0.41-0.31\right)},\frac{\frac{0.33}{0.39}}{\left(0.39-0.33\right)}\right]=\left[\mathrm{7.60,14.17}\right].$

3.2.2. Case (ii)

The line 2 follows Erlang -3 service time. The performance metrics can be evaluated with $k$ equal to $3$ in $NM/(NG\equiv N{E}_k)/1$ queue formula.

Performance measures of $NM/(NG\equiv N{E}_k)/1$ queueing models are:

1. Expected number of customers in the system:

37

${NL}_s=\left(\frac{k+1}{2k}\right)\left[\frac{{\left(\frac{{\lambda }_L}{{\mu }_U}\right)}^2}{\left(1-\frac{{\lambda }_L}{{\mu }_U}\right)},\frac{{\left(\frac{{\lambda }_U}{{\mu }_L}\right)}^2}{\left(1-\frac{{\lambda }_U}{{\mu }_L}\right)}\right]+\left[\frac{{\lambda }_L}{{\mu }_U},\frac{{\lambda }_U}{{\mu }_L}\right],$

38

${NL}_s=\left(\frac{3+1}{2*3}\right)\left[\frac{{\left(\frac{0.31}{0.41}\right)}^2}{\left(1-\frac{0.31}{0.41}\right)},\frac{{\left(\frac{0.33}{0.39}\right)}^2}{\left(1-\frac{0.33}{0.39}\right)}\right]+\left[\frac{0.31}{0.41},\frac{0.33}{0.39}\right]=\left[\mathrm{2.37,4.06}\right].$

2) Expected number of customers in the queue:

39

${NL}_q=\left(\frac{k+1}{2k}\right)\left[\frac{{\left(\frac{{\lambda }_L}{{\mu }_U}\right)}^2}{\left(1-\frac{{\lambda }_L}{{\mu }_U}\right)},\frac{{\left(\frac{{\lambda }_U}{{\mu }_L}\right)}^2}{\left(1-\frac{{\lambda }_U}{{\mu }_L}\right)}\right],$

40

${NL}_q=\left(\frac{3+1}{2*3}\right)\left[\frac{{\left(\frac{0.31}{0.41}\right)}^2}{\left(1-\frac{0.31}{0.41}\right)},\frac{{\left(\frac{0.33}{0.39}\right)}^2}{\left(1-\frac{0.33}{0.39}\right)}\right]=\left[\mathrm{1.61,3.21}\right].$

3) Expected waiting time of a customer in the system:

41

${NW}_s=\left(\frac{k+1}{2k}\right)\left[\frac{\frac{{\lambda }_L}{{\mu }_U}}{\left({\mu }_U-{\lambda }_L\right)},\frac{\frac{{\lambda }_U}{{\mu }_L}}{\left({\mu }_L-{\lambda }_U\right)}\right]+\left[\frac{1}{{\mu }_U},\frac{1}{{\mu }_L}\right],$

42

${NW}_s=\left(\frac{3+1}{2*3}\right)\left[\frac{\frac{0.31}{0.41}}{\left(0.41-0.31\right)},\frac{\frac{0.33}{0.39}}{\left(0.39-0.33\right)}\right]+\left[\frac{1}{0.41},\frac{1}{0.39}\right]=\left[\mathrm{7.51,12.01}\right].$

4) Expected waiting time of a customer in the queue:

43

${NW}_q=\left(\frac{k+1}{2k}\right)\left[\frac{\frac{{\lambda }_L}{{\mu }_U}}{\left({\mu }_U-{\lambda }_L\right)},\frac{\frac{{\lambda }_U}{{\mu }_L}}{\left({\mu }_L-{\lambda }_U\right)}\right],$

44

${NW}_q=\left(\frac{3+1}{2*3}\right)\left[\frac{\frac{0.31}{0.41}}{\left(0.41-0.31\right)},\frac{\frac{0.33}{0.39}}{\left(0.39-0.33\right)}\right]=\left[\mathrm{5.07,9.45}\right].$

3.2.3. Case (iii)

The line 3 follows deterministic service time. The performance metrics can be evaluated in $NM/(NG\equiv ND)/1$.

Performance measures of $NM/(NG\equiv ND)/1$ queueing models are:

1. Expected number of customers in the system:

45

${NL}_s=\left(\frac{1}{2}\right)\left[\frac{{\left({\lambda }_L\right)}^2}{{\mu }_U\left({\mu }_U-{\lambda }_L\right)},\frac{{\left({\lambda }_U\right)}^2}{{\mu }_L\left({\mu }_L-{\lambda }_U\right)}\right]+\left[\frac{{\lambda }_L}{{\mu }_U},\frac{{\lambda }_U}{{\mu }_L}\right],$

46

${NL}_s=\left(\frac{1}{2}\right)\left[\frac{{\left(0.31\right)}^2}{0.41\left(0.41-0.31\right)},\frac{{\left(0.33\right)}^2}{0.39\left(0.39-0.33\right)}\right]+\left[\frac{0.31}{0.41},\frac{0.33}{0.39}\right]=\left[\mathrm{1.93,3.18}\right].$

2) Expected number of customers in the queue:

47

${NL}_q=\left(\frac{1}{2}\right)\left[\frac{{\left({\lambda }_L\right)}^2}{{\mu }_U\left({\mu }_U-{\lambda }_L\right)},\frac{{\left({\lambda }_U\right)}^2}{{\mu }_L\left({\mu }_L-{\lambda }_U\right)}\right],$

48

${NL}_q=\left(\frac{1}{2}\right)\left[\frac{{\left(0.31\right)}^2}{0.41\left(0.41-0.31\right)},\frac{{\left(0.33\right)}^2}{0.39\left(0.39-0.33\right)}\right]=\left[\mathrm{1.17,2.33}\right].$

3) Expected waiting time of a customer in the system:

49

${NW}_s=\left(\frac{1}{2}\right)\left[\frac{{\lambda }_L}{{\mu }_U\left({\mu }_U-{\lambda }_L\right)},\frac{{\lambda }_U}{{\mu }_L\left({\mu }_L-{\lambda }_U\right)}\right]+\left[\frac{1}{{\mu }_U},\frac{1}{{\mu }_L}\right],$

50

${NW}_s=\left(\frac{1}{2}\right)\left[\frac{0.31}{0.41\left(0.41-0.31\right)},\frac{0.33}{0.39\left(0.39-0.33\right)}\right]+\left[\frac{1}{0.41},\frac{1}{0.39}\right]=\left[\mathrm{6.22,9.61}\right].$

4) Expected waiting time of a customer in the queue:

51

${NW}_q=\left(\frac{1}{2}\right)\left[\frac{{\lambda }_L}{{\mu }_U\left({\mu }_U-{\lambda }_L\right)},\frac{{\lambda }_U}{{\mu }_L\left({\mu }_L-{\lambda }_U\right)}\right],$

52

${NW}_q=\left(\frac{1}{2}\right)\left[\frac{0.31}{0.41\left(0.41-0.31\right)},\frac{0.33}{0.39\left(0.39-0.33\right)}\right]=\left[\mathrm{3.78,7.05}\right].$

Table 6Summary of results

Line	Line distribution	$N{L}_S$		$N{L}_q$		${NW}_s$		$N{W}_q$
		$N{L}_{SL}$	$N{L}_{SU}$	$N{L}_{qL}$	$N{L}_{qU}$	${NW}_{sL}$	${NW}_{sU}$	$N{W}_{qL}$	$N{W}_{qU}$
1	Neutrosophic exponential	3.17	5.67	2.41	4.82	10.04	16.73	7.60	14.17
2	Neutrosophic Erlang 3	2.37	4.06	1.61	3.21	7.51	12.01	5.07	9.45
3	Neutrosophic deterministic	1.93	3.18	1.17	2.33	6.22	9.61	3.78	7.05

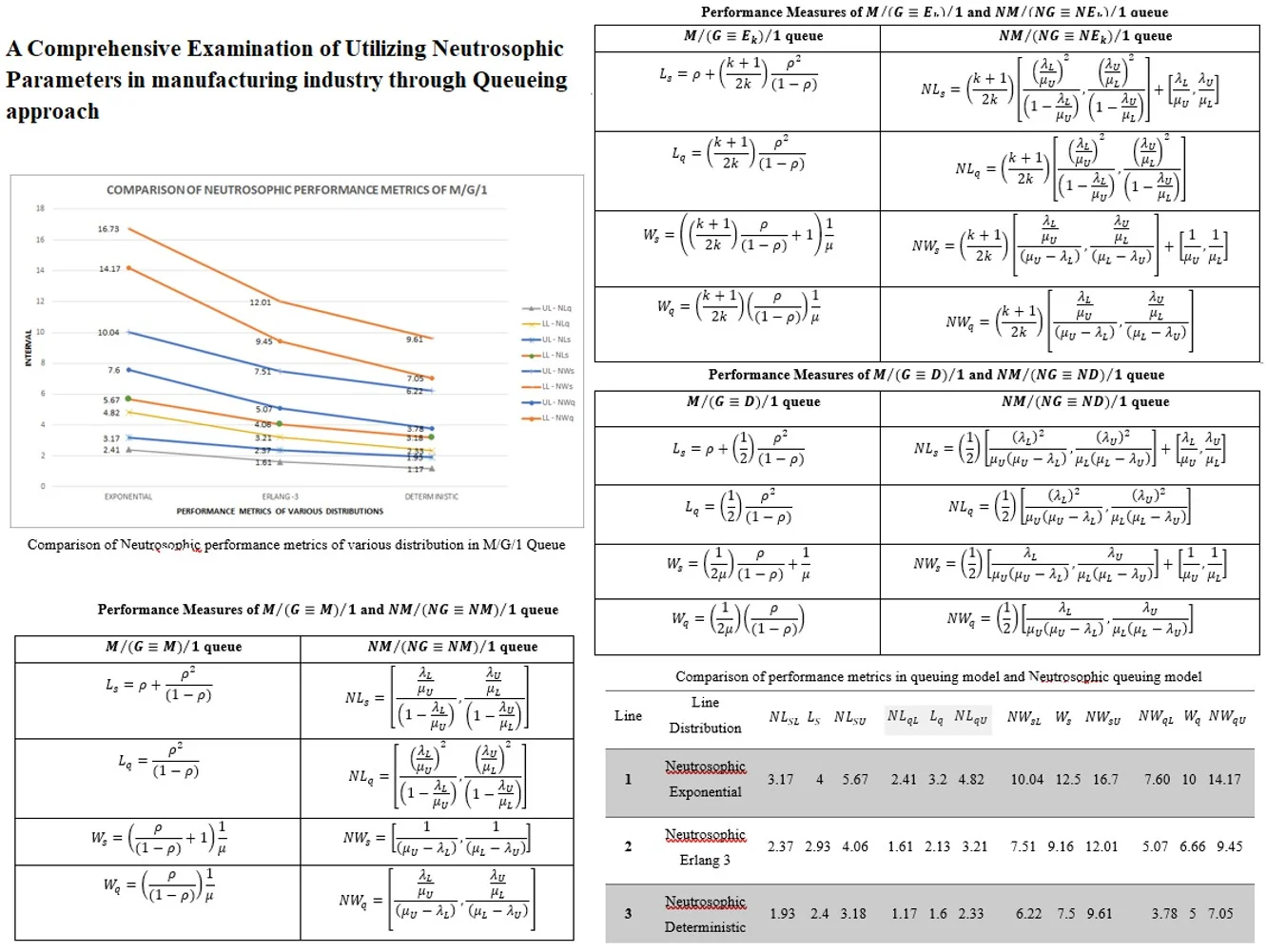
Fig. 1Comparison of Neutrosophic performance metrics of various distribution in M/G/1 Queue

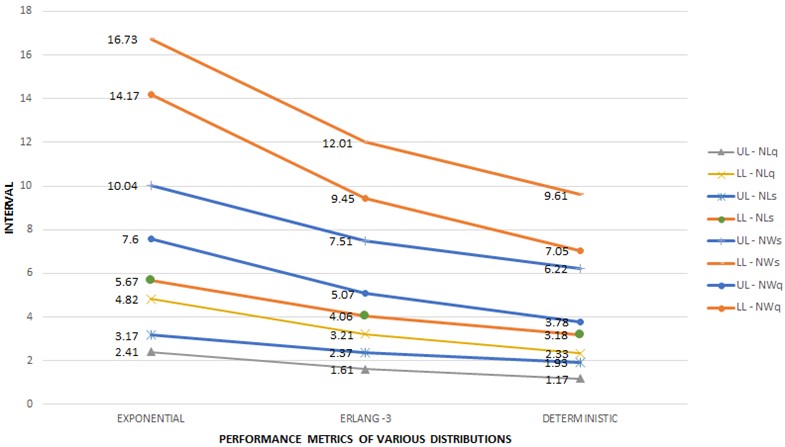
Table 7Comparison of performance metrics in queuing model and Neutrosophic queuing model

Line	Line distribution	$N{L}_{SL}$	$L_S$	$N{L}_{SU}$	$N{L}_{qL}$	$L_q$	$N{L}_{qU}$	${NW}_{sL}$	$W_s$	${NW}_{sU}$	$N{W}_{qL}$	$W_q$	$N{W}_{qU}$
1	Neutrosophic exponential	3.17	4	5.67	2.41	3.2	4.82	10.04	12.5	16.7	7.60	10	14.17
2	Neutrosophic Erlang 3	2.37	2.93	4.06	1.61	2.13	3.21	7.51	9.16	12.01	5.07	6.66	9.45
3	Neutrosophic deterministic	1.93	2.4	3.18	1.17	1.6	2.33	6.22	7.5	9.61	3.78	5	7.05

In the provided graph and table, it’s evident that the interval length between the expected queue length and system length, as well as the average number of customers waiting in the queue and system, is greater in the case of exponential service time compared to deterministic service time. Furthermore, the crisp data for each performance metric of each service time distribution falls within the interval length. This suggests that the neutrosophic queueing system exhibits the smallest interval length, particularly excelling in the deterministic scenario.

4. Conclusions

Analysis of performance metrics can inform future infrastructure investments and upgrades, guiding decisions on scaling or redesigning communication systems to accommodate growing demands and emerging technologies. Future work based on neutrosophic queueing theory involves refining modeling techniques to better capture complex uncertainties in diverse systems. This includes developing advanced algorithms for optimization, resource allocation, and decision-making, paving the way for more effective management strategies across Telecommunication Networks, Healthcare Systems, Supply Chain Management, Computer Systems, Transportation Systems, and Manufacturing Systems.