Study of the influencing factors that affect the measurement of thermal conductivity of graphene thin films

2.1. Measurement principle

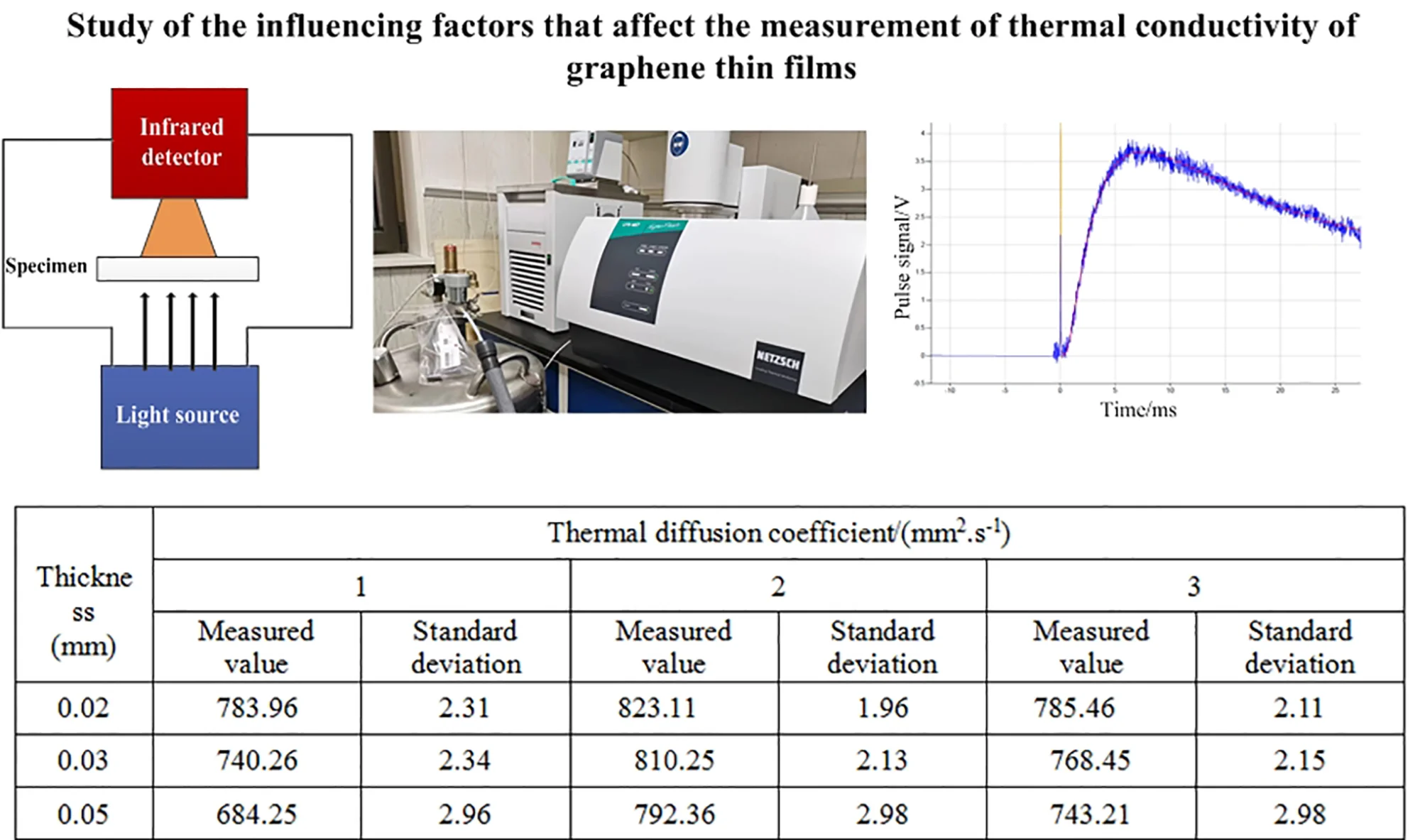
The thermal diffusivity of graphene films can be measured directly by using laser flash method. The light source emits a pulse instantaneously and uniformly irradiates on the lower surface of the graphene film, causing the temperature to rise instantaneously after the surface layer absorbs energy. The energy is then propagated to the upper surface of the graphene film by one-dimensional heat conduction. The corresponding heating process of the center part of the upper surface of the graphene film is continuously recorded with an infrared detector, and the change curve of the temperature detection signal with time is obtained. The time $t_{1/2}$ (half heating time) required for the upper surface temperature of the graphene film to rise to half of the maximum temperature appreciation $T_M$ can be obtained. The measurement principle diagram is shown in Fig. 1.

Fig. 1Schematic diagram of thermal diffusion coefficient test for graphene films

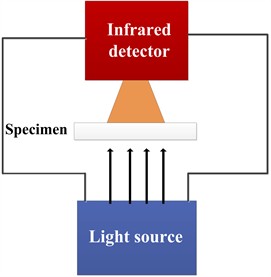
a) Schematic diagram of instrument

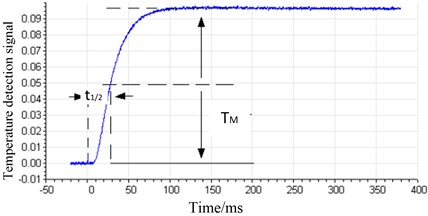
b) Temperature curve

The thermal diffusivity of the material is calculated according to Fourier heat transfer equation, as shown in Eq. (1):

where, $\alpha$ is expressed as the thermal diffusivity, mm²/s; $L$ is the thickness of the sample, mm; $t_{1/2}$ is the half heating time, s.

The thermal conductivity $\lambda$ can be calculated from Eq. (2):

where, $\lambda$ is expressed as thermal conductivity, $c$ is the specific heat; $\rho$ is the density.

2.2. Measurement method

The ambient temperature of the laboratory is 20 °C, the ambient humidity is 50 % RH, and there is no obvious vibration and shock around the instrument. The technical requirements of instruments and supporting equipment used in the test process can be shown in Table 1 and Fig. 2.

Fig. 2Testing instrument

The test process is operated according to the national standard GB/T22588-2008 “Flash method to measure the thermal diffusion coefficient or thermal conductivity” and JJF145-2024 “Technical norm for measurement of thermal diffusivity of graphene heat sinks”, which can ensure the accuracy and repeatability of the experimental data. The testing process can be described in detail as follows:

Turn on the device and stabilize it for 10 minutes or meet the requirements of its instruction manual; The surface of the graphene film should be flat, and the parallelism error should be within 0.5 % of the thickness. And the surface of the film is not allowed to have any sand holes, scratches, streaks defects.

Firstly, the thickness of the graphene film is measured 3 times by micrometer, then the arithmetic mean value L of the measured result is taken as its thickness value.

Secondly, the upper and lower surfaces of the graphene film are sprayed with thin and uniform graphite to cover the surface luster of the graphene film.

Thirdly, Set the laser voltage, pulse width and sample thickness in the instrument to ensure that the temperature rise curve height should be in the range of (3-10) V.

Finally, the measurement of the graphene film is repeated 3 times, and the average value is taken as the final measurement value.

In subsequent experiments, the influence of different factors such as spray graphite, pulse width, thickness, and measurement direction on measurement accuracy will be carefully analyzed. The parameter settings in different subsequent experiments can be shown in Table 2.

The formula for calculating the thermal diffusion coefficient of the graphene heat sink is as follows:

where $\overline{Y}$ is the average thermal diffusion coefficient of graphene film; $Y_i$ is the measured value of the thermal diffusion coefficient of the $i$; $n$ is number of measurements.

The repeatability of the thermal diffusion coefficient is expressed by the standard deviation, and the calculation formula is shown as follows:

where $s$ is repeatability/Standard deviation, mm²/s; $\overline{Y}$ is average value of thermal diffusivity, mm²/s; $Y_i$ is measurement results of thermal diffusivity for the $i$ time, mm²/s; $n$ is number of measurements.

2.3. Uncertainty measurement method

The uncertainty measurement model is shown as follows:

where $L$ is the thickness of the graphene film, mm; $Y$ is thermal diffusivity, mm²/s; $t_{1/2}$ is the time when the temperature of the upper surface of the graphene film rises to half the maximum time.

The main sources of thermal diffusivity uncertainty include the following items:

(1) The relative repeated uncertainty introduced by thermal diffusivity $u_{1r}\left(Y\right)$.

(2) The relative uncertainty introduced by thickness $u_r\left(L\right)$.

(3) The relative uncertainty introduced by the half-heating time $u_r\left(t\right)$.

The relative synthetic uncertainty of the thermal diffusivity is expressed as follows:

3.1. Effect of graphite spray on measurement results

Six graphene film samples were selected to test their thermal diffusivity under two conditions: graphite spray and no graphite spray. Experimental parameters are set according to case 1 in Table 3. The test results are shown as follows.

Fig. 3Signal fitting curve of six samples without graphite

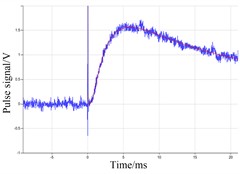
a)

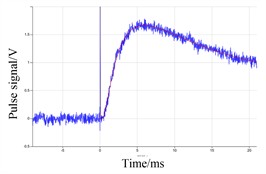
b)

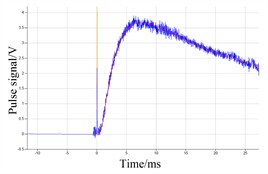
c)

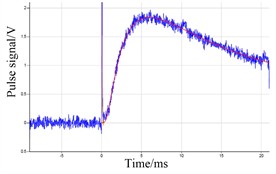
d)

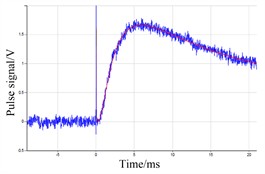
e)

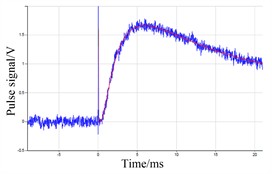
f)

From Fig. 3 and Table 3, it can be seen that when the samples are not coated with graphite, the standard deviation measured by the six samples is a little large, and the corresponding fitted signal will have a large signal to noise ratio (SNR). The thermal diffusivity of the six samples are 782.9923 mm²/s, 882.3743 mm²/s, 882.3743 mm²/s, 783.3097 mm²/s, 783.3097 mm²/s, 882.3117 mm²/s, respectively. The standard deviations of the six samples ranged from 4 to 9. The appearance of the SNR is due to the fact that the sample surface is not coated with graphite, and the surface is not smooth, this will cause some of the energy to reflected away.

It can be seen from the results of Fig. 4 and Table 4, compared with the results of Fig. 4 and Table 4. When the six samples are sprayed with graphite, the thermal diffusivity of the six samples are 783.325 mm²/s, 885.707 mm²/s, 789.977 mm²/s, 789.977 mm²/s, 789.977 mm²/s, 886.645 mm²/s respectively. The standard deviation is range between 0.881 mm²/s and 3.155 mm²/s. Compared with the results in Fig. 3 and Table 3, the measured values did not change significantly, but the standard deviation is significantly smaller, indicating that the surface of the sample is smooth due to the coating of graphite, which can be better to reduce light reflection. In the case of sprayed graphite, the repeatability of the data becomes better than that without sprayed graphite, and the measurement accuracy would be improved under the condition of spraying graphite.

Fig. 4Signal fitting curve of six samples with graphite

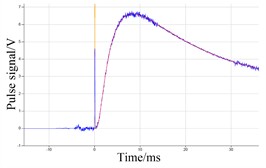
a)

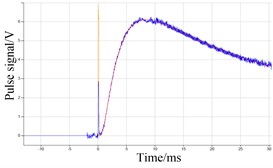
b)

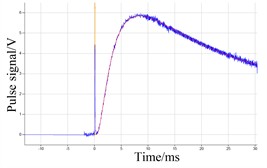
c)

d)

e)

f)

3.2. Influence of different pulse widths on test results

Three 25 μm commercial graphene films are selected to analyze the effect of different pulse widths on measurement accuracy. the instrument detector is MTC, the pulse voltage is 260 V, the pre-stage gain is 10000, the main gain and pulse time are automatically optimized during the measurement process, and the calculation model is In-plane+Isotropic mode, experimental parameters are set according to case 2 in Table 2. The thermal diffusivity of four graphene films are measured at pulse widths of 20 μs, 50 μs, 100 μs and 250 μs, respectively.

Table 5 shows the measured values of three different samples at pulse widths of 20 μs, 50 μs, 100 μs, 250 μs. From the data of sample 1, as the pulse width increases from 20 μs to 250 μs, the measured value gradually decreases and the standard deviation gradually increases, which indicates that the smaller the pulse width can be obtained the larger the measured value and the smaller the standard deviation, which means the higher the measurement accuracy can be obtained at pulse widths of 20 μs.

The same rule can be obtained from the measurement results of sample 2 and sample 3. The increase of pulse width will lead to the increase of measurement value. The reduction of standard deviation means the improvement of measurement accuracy.

3.3. Influence of sample thickness on test results

In this experiment, three samples are selected and processed into four kinds of thickness: 0.02 mm, 0.03 mm, 0.05 mm and 0.10 mm, respectively. Experimental parameters are set according to case 3 in Table 2. The results of thermal diffusivity of graphene films with different thicknesses can be obtained in Table 7.

It can be seen the results in Table 6: the results of sample 1 shows that as the thickness of the graphene film increases from 0.02 mm to 0.10 mm, the measured value changes from 783.96 mm².s^-1 to 642.12 mm².s^-1, the standard deviation becomes larger, which will results in the smaller measurement accuracy.

A similar rule can be obtained in sample 2 and sample 3, thinner graphene film will bring higher measurement value and smaller standard deviation. When the film thickness of sample 2 changes from 0.02 mm to 0.10 mm, the thermal diffusivity of sample 2 decreases from 823.11 mm²/s to 772.45 mm²/s, and the measurement value of sample 3 increases from 721.12 mm²/s to 785.46 mm²/s. It can be found that thinner graphene films lead to higher measurement results, smaller standard deviations, and higher measurement accuracy.

3.4. Measurement results of different measurement directions

Five samples with thickness of 0.02 mm, 0.025 mm, 0.03 mm, 0.035 mm and 0.040 mm are selected to analyze the influence of different measurement directions on measurement accuracy. Experimental parameters are set according to case 4 in Table 2. The results of thermal diffusivity of graphene films with different thicknesses can be obtained as shown in Table 7.

Table 7 shows that when sample 1 is measured, the measurement value of thermal diffusivity is 765.32 mm²/s and the standard deviation is 1.12 mm²/s in the in-plane direction. When the measurement direction is out of plane, the thermal diffusivity is 5.32 mm²/s and the standard deviation is 0.32 mm²/s. The results show that the thermal diffusivity in the in-plane direction is much larger than that in the out-of-plane direction.

In the in-plane direction, the thermal diffusivity of samples of 2, 3, 4 and 5 are 832.45 mm²/s, 756.45 mm²/s, 756.45 mm²/s and 865.24 mm²/s, respectively. In the out-plane direction, the thermal diffusivity of samples of 2, 3, 4, and 5 are 7.62 mm²/s, 5.32 mm²/s, 4.35 mm²/s, and 7.52 mm²/s, respectively. These results also show that the thermal diffusivity of the five samples in the in-plane direction is much larger than that in the out-of-plane direction, the measurement results in the in-plane direction are about 140 times greater than that in the out-of-plane direction.

3.5. Uncertainty result

In order to further verify the above measurement results, 10 repeated measurements are made on the graphene film under the condition of pulse width of 50 um, and the uncertainty are studied under the condition of spray graphite and non-spray graphite at different measurement directions, as shown in Table 8.

Looking at the first case in Table 8, the results show that the synthetic uncertainty is at least 2.06 % when the graphene film is 0.02 mm and sprayed with graphite. From the case 2, when the film thickness is 0.10 mm, the thickness uncertainty increases to 0.35 %, and the synthetic uncertainty can reach 2.14 %. This means that the increase of thickness greatly affects the uncertainty results of thickness, which will greatly increases the synthetic uncertainty. Seen from the case 3, when the measured thickness of the graphene film is 0.02 mm and the surface of the film is not coated with graphite, compared with case 1, the repeatability of measurement uncertainty is increased to 0.41, and the synthetic uncertainty is 2.08 %, which is similar with that of the first case.

In case 4, it can be seen that when the graphene film is 0.02 mm, the graphite is sprayed and the measurement direction is out of plane, the uncertainty of measurement repeatability increases to 0.52 % and the synthetic uncertainty is 2.11 %.