Estimation of vehicle state based on improved dual layer UKF

Wang, Qianqian; Liu, Yingjie; Cui, Dawei

doi:10.21595/jme.2026.25025

Journal of Measurements in Engineering

Browse Journal

Submit article

Published: February 6, 2026

Check for updates

Estimation of vehicle state based on improved dual layer UKF

Qianqian Wang¹

Yingjie Liu²

Dawei Cui³

^{1, 2, 3}School of Machinery and Automation, Weifang University, Weifang, 261061, Shandong, China

^{1, 2, 3}Shandong Key Laboratory of Intelligent Manufacturing Technology for Advanced Power Equipment, Weifang, 261061, Shandong, China

Corresponding Author:

Yingjie Liu

Cite the article Download PDF

Article in Press

Downloads 0

Abstract

In order to address the issue of lower estimation accuracy of traditional methods, an adaptive dual layer unscented Kalman filter algorithm (ADLUKF) is proposed, which combines the dual layer unscented Kalman filter (DLUKF) with an improved Sage-Husa algorithm to estimate the states and reduce the error in vehicle driving state estimation. The Carsim and Matlab/Simulink for joint simulation is applied and real vehicle test is established to verify the effectiveness of the estimator, and compare it with the Unscented Kalman Filter (UKF) algorithm. The results indicate that the ADLUKF algorithm can improve the estimation accuracy of vehicle estimation effectively.

Highlights

The ADLUKF algorithm can improve the estimation accuracy of vehicle estimation effectively.
The proposed adaptive dual layer unscented Kalman filter algorithm(ADLUKF) algorithm can solve the problem of vehicle state estimation with the performance of higher estimation accuracy.
The ADLUKF has higher estimation accuracy for yaw rate and side slip angle as well as longitudinal velocity.

1. Introduction

The estimation of the state parameters of vehicles during driving has always been a focus of attention for researchers in the automotive industry both domestically and internationally. At present, the most widely used is the Kalman filter algorithm (KF) and its derived estimation methods. Kalman filtering enables confidence calculation of continuous states in linear systems. It is currently the most widely used state estimation and filtering method. From the existing research results, it can be seen that linear dynamics models can no longer fully meet the estimation requirements of vehicle motion parameters. With the vigorous development of autonomous driving technology and further expansion of vehicle usage scenarios, as well as the requirements of vehicle active and passive safety technology, state estimation of vehicle nonlinear dynamics models has gradually become a research hotspot. The widely used estimator techniques include nonlinear Kalman filters, non current state observers, and artificial intelligence methods. The EKF discretizes nonlinear systems and converts them into linear systems. When the system is in strong nonlinearity, there is a significant estimation bias, and the estimation results are prone to divergence. It has the advantages of no need to process the Jacobian matrix, high computational accuracy, and high stability [1-3].

Li et al. proposed an improved Sage-Husa EKF method using wheel speed as the input signal and estimated the vehicle state parameters [4]. Wang et al. utilized fuzzy control theory to perform online real-time adjustment of measurement noise, improving the robustness of the algorithm [5]. Li et al. studied a state estimation algorithm using the robust volume Kalman filter theory with anti outliers, taking into account the easy availability of four-wheel torque and speed in electric vehicles driven by distributed four-wheel hub motors [6]. The application of neural networks in estimating the adhesion coefficient of road surfaces has become a research hotspot for many scholars. Neural networks have great advantages in dealing with nonlinear problems and meet the needs of estimating road adhesion coefficients [7-10]. In recent years, the most widely used algorithms for estimating road adhesion coefficients are the EKF and UKF. The research focus has gradually shifted from traditional fuel vehicles to wheel driven electric vehicles. Enisz et al. established a two wheel dynamic model of a vehicle and designed a filter using the discrete-time extended Kalman filter algorithm [11]. Li Gang et al. estimated the state variables of vehicle driving changes through federated Kalman filtering [12]. By forming a closed-loop feedback between vehicle state variables and road adhesion coefficient, adaptive adjustment was achieved, and simulation verification was carried out. Liu et al. used auxiliary particle filtering to preliminarily estimate the side slip angle of a vehicle and improved and optimized the preliminarily estimated side slip angle using iterative EKF algorithm [13]. Based on this, they combined self centering torque and iterative EKF algorithm to achieve real-time estimation of road adhesion coefficient. Wang et al. studied the observation algorithm of electric wheel drive vehicles and established an 8-DOF vehicle model. By reducing the sampling points, the convergence rate of the UKF algorithm was improved, and the estimation of road adhesion coefficient was achieved [14]. However, the estimation results of road adhesion coefficient were easily affected by noise characteristics. In order to obtain more accurate estimation of road adhesion coefficient, Fu et al. studied four-wheel independent drive off-road vehicles and introduced memory decay filtering for optimization based on the UKF algorithm and compared the simulated output values with real vehicle experiments [15]. Zhao et al. proposed an unscented Kalman filtering algorithm suitable for the characteristics of wheel hub motor-driven electric vehicles [16]. This algorithm was used to estimate the speed information but had not judged and corrected the divergence of the algorithm. Boada et al. designed a dual layer side slip angle observer based on adaptive neural fuzzy inference algorithm and UKF algorithm. The upper layer estimated the side slip angle information based on the already configured inertial sensors and steering wheel angle sensors of the vehicle, using adaptive neural fuzzy inference algorithm [17]. Massarelli et al. applied filtering algorithms to indirect bridge structural health monitoring [18-20].

Due to the complex driving environment of vehicles, most traditional estimation algorithms currently do not adjust the system noise in real time, and it is often difficult to obtain the characteristics of system noise in practice. At the same time, although UKF has higher estimation accuracy and better stability than EKF, in the traditional process of estimating vehicle state parameters using UKF, the process noise covariance matrix $Q$ and measurement noise covariance matrix $R$ are treated as constant matrices. The covariance matrix $Q$ of process noise has certain robustness and has a small impact on the filtering estimation effect, while measurement noise is mainly affected by external conditions and has a large degree of uncertainty. Slight changes in the covariance matrix $R$ of measurement noise can have a significant impact on the filtering effect. Therefore, in this article, the improved Sage-Husa adaptive filtering algorithm is combined with the DLUKF algorithm to form the adaptive double layer unscented Kalman filter algorithm. By adaptively adjusting the process noise and measurement noise of the system, it is possible to reduce the estimation error of the vehicle driving state and improve the estimation accuracy of key parameters such as yaw rate and side slip angle. Meanwhile, the algorithm can adapt to different environments and system changes, effectively addressing issues such as system noise uncertainty, and enhancing the stability and robustness of filtering. This algorithm updates the system noise in real-time while estimating the vehicle states, thereby improving the accuracy of vehicle states estimation and system stability.

2. Mathematical model of vehicle dynamics

2.1. 3-DOF vehicle model

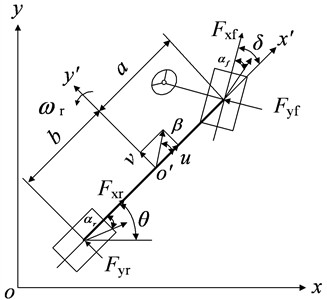
The vehicle state estimation model is established based on a 3-DOF vehicle model.

The dynamic equation of the 3-DOF vehicle model is as follows [21]:

1

{\dot{ω}}_{r} = \frac{a^{2} k_{1} + b^{2} k_{2}}{I_{z}} \frac{ω_{r}}{u} + \frac{a k_{1} + b k_{2}}{I_{z}} β - \frac{a k_{1}}{I_{z}} δ,

2

\dot{β} = \frac{a k_{1} + b k_{2} - m u^{2}}{m} \frac{ω_{r}}{u^{2}} + \frac{k_{1} + k_{2}}{m} \frac{β}{u} - \frac{k_{1} δ}{m u},

3

\dot{u} = a_{x} + v x,

4

a_{y} = \frac{a k_{1} - b k_{2}}{m u} ω_{r} + \frac{k_{1} + k_{2}}{m} β - \frac{k_{1}}{m} δ .

The side slip angle is:

5

β = \arctan (\frac{v}{u}) .

Fig. 13-DOF vehicle model

2.2. Tire model

The lateral forces of front and rear wheels can be expressed as [22]:

6

\{\begin{matrix} F_{y f} = c_{f} α_{f}, \\ F_{y r} = c_{r} α_{r}, \end{matrix}

where $c_{f}$ and $c_{r}$ are the lateral stiffness values of the front and rear tires. $α_{f}$ and $α_{r}$ are the front and rear slip angles:

7

\{\begin{matrix} c_{f} = \frac{\partial F_{y f}}{\partial α_{f}}| α_{f} = 0, \\ c_{r} = \frac{\partial F_{y r}}{\partial α_{r}}| α_{r} = 0 . \end{matrix}

3. The ADLUKF algorithm

3.1. Standard UKF algorithm

The nonlinear systems can be represented by state equations:

8

\{\begin{matrix} x (k + 1) = f (x (k), u (k) + w (k)), \\ z (k) = h (x (k), u (k) + v (k)), \end{matrix}

where $f (\cdot)$ and $h (\cdot)$ are both nonlinear functions.

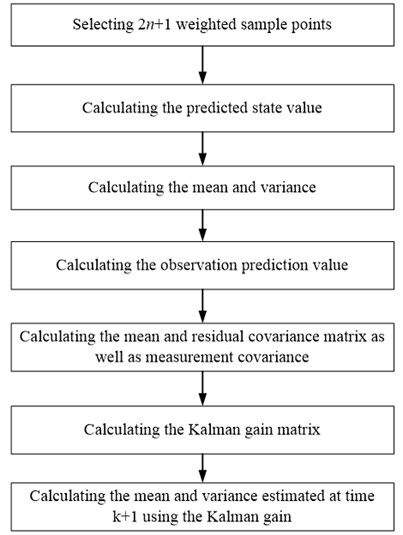
The UKF algorithm can be briefly described as follows:

Step 1. Selecting $2 n + 1$ weighted sample points.

Step 2. The predicted state value $x_{(i)} (k + 1 |k)$ for sample point $x_{(i)} (k |k)$ can be obtained through a nonlinear function $f (\cdot)$ .

Step 3. The mean and variance can be obtained by weighted sum of $x_{(i)} (k + 1 |k)$ .

Step 4. The observation prediction value $z_{(i)} (k + 1 |k)$ can be obtained through the nonlinear function $h (\cdot)$ .

Step 5. The mean $\bar{z}$ and residual covariance matrix $P_{z_{k} z_{k}}$ as well as measurement covariance $P_{x_{k} z_{k}}$ are obtained.

Step 6. Calculating the Kalman gain matrix $K$ from the residual covariance and measurement covariance.

Step 7. Calculating the mean and variance estimated at time $k + 1$ using the Kalman gain.

The flow chart of the algorithm is shown in Fig. 2.

Fig. 2Flow chart of the UKF algorithm

3.2. Dual layer UKF algorithm

In this article, the dual layer unscented Kalman filter algorithm is used to solve the problem.

1) Calculating the sample points and their weights.

It is assumed that the mean and covariance of the state distribution are $\bar{x}$ and $P_{k}$ respectively. N sampling points are selected using a symmetric sampling strategy [23, 24]:

9

\{\begin{matrix} x_{(i)} = \bar{x}, i = 0, \\ x_{(i)} = \bar{x} + (\sqrt{(n + λ) P_{k}})_{i}, i = 1,2, \dots, n, \\ x_{(i)} = \bar{x} - (\sqrt{(n + λ) P_{k}})_{i}, i = n + 1, n + 2, \dots, 2 n m \end{matrix}

10

λ = α^{2} (n + κ) - n,

where $λ$ is the scaling factor; $x$ is an $n$ -dimensional state variable; $α$ and $κ$ are both values to be taken. Normally, $α$ takes a smaller positive value, which determines the distribution of sampling points. When $n > 3$ , $κ$ is zero, and when $n \leq 3$ $κ$ is the difference.

Then the weights corresponding to the sampling points is calculated:

11

\{\begin{matrix} ω_{0}^{(m)} = \frac{λ}{n + λ}, \\ ω_{0}^{(c)} = \frac{λ}{n + λ} + (1 - α^{2} + β), \\ ω_{i}^{(m)} = W_{i}^{(c)} = \frac{1}{2 (n + λ)}, i = 1, \dots, 2 n, \end{matrix}

where $β \geq 0$ .

2) Inner UKF.

For each particle in the outer layer, $2 n + 1$ weighted sample points ${\{x_{j, i, k}\}}_{j = 1}^{2 n + 1}$ are selected using the above sampling method.

The predicted state value of weighted particles can be obtained according to the state equation of the system:

12

x_{j, i, k + 1 | k} = f (x^{(i)} (k| k), u (k)), j = 1,2, \dots, 2 n + 1 .

The mean and variance of the predicted particle states can be obtained by summing up the predicted weighted particle states by Eq. (9):

13

{\bar{x}}_{i, k + 1 | k} = \sum_{j = 0}^{2 n} ω_{i}^{(m)} x_{j, i, k + 1 | k} + q_{k},

14

P_{i, k + 1 | k} = \sum_{i = 0}^{2 n} ω_{i}^{(c)} (x_{j, i, k + 1 | k} - {\bar{x}}_{i, k + 1 | k}) \times (x_{j, i, k + 1 | k} - {\bar{x}}_{i, k + 1 | k})^{T} + Q_{k},

where $q_{k}$ is the mean value of system process noise.

Based on the above prediction of mean and variance of the weighted particle, $2 n + 1$ sampling points ${\{x_{j, i, k + 1 |k}^{0}\}}_{j = 1}^{2 n + 1}$ and their mean and variance weights $ω_{j, i, k + 1 |k}^{m}$ and $ω_{j, i, k + 1 |k}^{c}$ are obtained using the sampling methods of Eqs. (1)-(4) and Eq. (8). The observation prediction value of weighted particles can be obtained according to the observation equation of the system:

15

z_{j, i, k + 1 | k} = h (x_{j, i, k + 1 | k}^{0}, u (k)), j = 1,2, \dots, 2 n + 1 .

The mean ${\bar{z}}_{i, k + 1 |k}$ and residual covariance matrix $P_{i, z_{k} z_{k}}$ and measurement covariance $P_{i, x_{k} z_{k}}$ of observation and prediction can be obtained by weighting and summing the observation and prediction values of the weighted particles obtained from Eq. (12):

16

{\bar{z}}_{i, k + 1 | k} = \sum_{j = 0}^{2 n} ω_{i}^{(m)} z_{j, i, k + 1 | k} + r_{k},

17

P_{i, z_{k} z_{k}} = \sum_{i = 0}^{2 n} ω_{i}^{(c)} (z_{j, i, k + 1 | k} - {\bar{z}}_{i, k + 1 | k}) \times (z_{j, i, k + 1 | k} - {\bar{z}}_{i, k + 1 | k})^{T} + R_{k},

18

P_{i, x_{k} z_{k}} = \sum_{i = 0}^{2 n} ω_{i}^{(c)} (x_{j, i, k + 1 | k} - {\bar{z}}_{i, k + 1 | k}) \times (z_{j, i, k + 1 | k} - {\bar{z}}_{i, k + 1 | k})^{T},

where $r_{k}$ is the mean value of observation noise of the system.

The Kalman gain matrix $K_{i, k + 1 | k}$ is calculated:

19

K_{i, k + 1 | k} = P_{i, x_{k} z_{k}} P_{i, z_{k} z_{k}}^{- 1} .

The outer particles can be updated to:

20

{\bar{x}}_{i, k + 1 | k + 1} = {\bar{x}}_{i, k + 1 | k} + K_{i, k + 1 | k} \times (z_{k + 1} - {\bar{z}}_{i, k + 1 | k}),

21

P_{i, k + 1 | k + 1} = K_{i, k + 1 | k} P_{i, z_{k} z} K_{i, k + 1 | k}^{T} + P_{i, k + 1 | k} .

3) Outer UKF.

The mean and variance of the predicted states of the outer particles can be updated to:

22

{\bar{x}}_{k + 1 ∣ k} = \sum_{i = 0}^{2 n} ω_{i}^{(m)} {\bar{x}}_{i, k + 1 ∣ k + 1} + q_{k},

23

P_{k + 1 | k} = \sum_{i = 0}^{2 n} ω_{i}^{(c)} ({\bar{x}}_{i, k + 1 | k + 1} - {\bar{x}}_{k + 1 | k}) \times ({\bar{x}}_{i, k + 1 | k + 1} - {\bar{x}}_{k + 1 | k})^{T} + Q_{k} .

The observation prediction values based on the particle states and corresponding weights updated by the inner UKF are updated as:

24

z_{i, k + 1 | k} = h ({\bar{x}}_{i, k + 1 | k + 1}, u (k)),

25

{\bar{z}}_{k + 1 | k} = \sum_{i = 0}^{2 n} ω_{i}^{(m)} z_{i, k + 1 | k} + r_{k},

26

P_{z_{k} z_{k}} = \sum_{i = 0}^{2 n} ω_{i}^{(c)} (z_{i, k + 1 | k} - {\bar{z}}_{k + 1 | k}) \times (z_{i, k + 1 | k} - {\bar{z}}_{k + 1 | k})^{T} + R_{k},

27

P_{x_{k} z_{k}} = \sum_{i = 0}^{2 n} ω_{i}^{(c)} ({\bar{x}}_{i, k + 1 | k + 1} - {\bar{z}}_{k + 1 | k}) \times (z_{i, k + 1 | k} - {\bar{z}}_{k + 1 | k})^{T} .

The Kalman gain matrix is calculated:

28

K_{k + 1 | k} = P_{x_{k^{z_{k}}}} P_{z_{k^{z_{k}}}^{- 1}} .

Finally, the estimated state vector and covariance based on the measured values at time $k + 1$ are updated:

29

x_{k + 1} = {\bar{x}}_{k + 1 | k} + K_{k + 1 | k} \times (z_{k + 1} - {\bar{z}}_{k + 1 | k}),

30

P_{k + 1} = P_{k + 1 | k} + K_{k + 1 | k} P_{z_{k} z_{k}} K_{k + 1 | k}^{T} .

3.3. ADLUKF

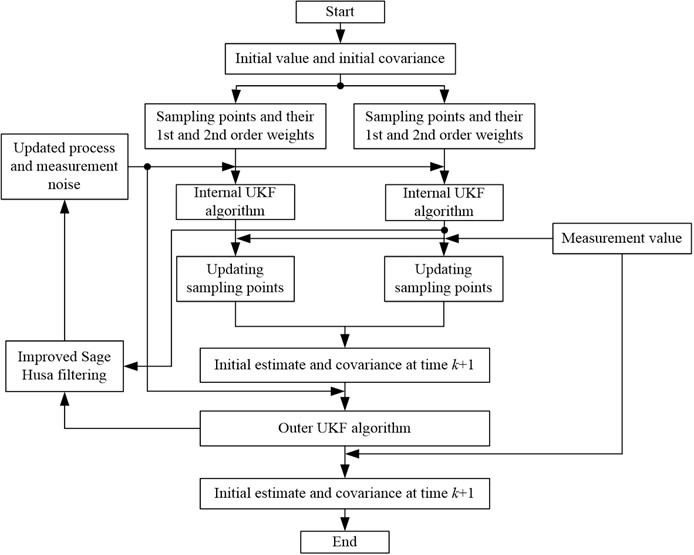
In actual driving, the movement of vehicles is affected by various factors such as road conditions, wind speed, and mechanical vibrations of the vehicle itself, which can generate complex noise. The improved Sage-Husa method assumes that the statistical characteristics of noise are unknown and time-varying, but in actual driving, due to the constantly changing driving environment, the statistical characteristics of noise are indeed difficult to determine in advance and change over time. For example, when driving on different road conditions (such as highways and rural roads), the noise interference received by vehicle sensors varies, and the statistical characteristics will also change. This method can adaptively estimate the statistical characteristics of noise by real-time calculation and correction of adjustment factors for filtering anomaly determination, thus meeting the time-varying requirements of noise characteristics in actual driving [25].

1) Mean Estimation of process noise:

31

q_{k + 1} = (1 - d_{k}) q_{k} + d_{k} (x_{k + 1} - \sum_{i = 0}^{2 n} ω_{i}^{(m)} x_{i, k + 1 | k}),

where:

32

d_{k} = \frac{1 - b}{1 - b^{k + 1}},

where $b$ is the forgetting factor.

2) Covariance estimation of process noise:

33

Q_{k + 1} = (1 - d_{k}) Q_{k} + d_{k} [K_{k + 1} e_{k} e_{k}^{T} K_{k + 1}^{T} + P_{k + 1}

- \sum_{i = 0}^{2 n} ω_{i}^{(c)} (x_{i, k + 1 | k} - {\bar{x}}_{k + 1 | k}) \times {(x_{i, k + 1 | k} - {\bar{x}}_{k + 1 | k})}^{T}],

34

e_{k} = z_{k + 1} - {\bar{z}}_{k + 1 | k} .

3) Mean Estimation of observation noise:

35

r_{k + 1} = (1 - d_{k}) r_{k} + d_{k} (z_{k + 1} - \sum_{i = 0}^{2 n} ω_{i}^{(m)} z_{i, k + 1 | k}) .

4) Covariance estimation of observation noise:

36

R_{k + 1} = R_{k} + d_{k} [e_{k + 1} e_{k + 1}^{T} - \sum_{i = 0}^{2 n} ω_{i}^{(c)} (z_{i, k + 1 | k} - {\bar{z}}_{k + 1 | k}) \times (z_{i, k + 1 | k} - {\bar{z}}_{k + 1 | k})^{T}] .

From Eqs. (30)-(33), it can be seen that the noise covariance matrix of the system cannot guarantee non negative definiteness. So $P_{k}$ may be a non positive definite matrix, which will result in the inability to obtain result from Eq. (1), ultimately leading to the failure of the ADLUKF algorithm in estimating the vehicle state.

In addition, both $Q_{k}$ and $R_{k}$ are uncorrelated Gaussian matrices and should be diagonal matrices. Therefore, adjustments need to be made to $Q_{k + 1}$ and $R_{k + 1}$ as follows:

37

Q_{k + 1} = \sqrt{d i a g (d i a g (Q_{k + 1} Q_{k + 1}^{T}))},

38

R_{k + 1} = \sqrt{diag (diag (R_{k + 1} R_{k + 1}^{T}))},

where $d i a g (\cdot)$ is the diagonal matrix composed of the main diagonal elements of $(\cdot)$ .

This algorithm can ensure the effective estimation of vehicle driving state parameters, not only reducing the impact of system noise on the estimation results but also improving the stability of vehicle driving state parameter estimation.

The flow chart of the algorithm is shown in Fig. 3.

Fig. 3Flow chart of the algorithm

4. Numerical simulation and experimental verification

4.1. Numerical simulation

Carsim is a software developed by MSC (Mechanical Simulation Corporation) using Vehicle Sim technology specifically for vehicle dynamics. Using CarSim to design, develop, test, and plan automotive projects enables better decision-making involving vehicle dynamics and takes less time. Carsim can be used to demonstrate the expected vehicle operating results and provide a more in-depth analysis of the current operating results.

The main features of Carsim software are as follows:

1) Easy to use.

Carsim has a modern graphical user interface that allows for running simulation experiments, watching animations or viewing the results of engineering drawings. Carsim Quick Start Guide takes about an hour to establish new operating conditions. The output curves and animations can be easily obtained by clicking the mouse, and the resulting graphics can be easily inserted into reports and PowerPoint presentations. The mathematical models of Carsim have been parameterized, including parameters commonly used by OEMs and suppliers. Therefore, Carsim users can obtain the operating results of new working conditions in the shortest possible time.

2) A large number of instance datasets and animated graphics.

Carsim has over 15 different vehicle models: A to F-class passenger cars, some vans, multi-purpose vehicles, and light trucks. Carsim has many test program samples and over 20 types of 3D vehicle shape files to ensure simulation animations. Each 3D vehicle can automatically adjust its size to match the size of the model car, and the color of the entire vehicle can be automatically reset during operation to distinguish vehicles under different working conditions.

4.1.1. Double lane changing condition

Figs. 4(a)-(d) show the simulation results under the double lane changing condition. And the common path tracking methods such as fuzzy adaptive unscented Kalman filter (FAUKF) and CKF are used to compared with the proposed algorithm.

Fig. 4Simulation results under double lane changing condition

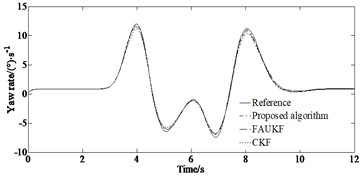
a) Yaw rate

b) Side slip angle

c) Longitudinal speed

d) Mean of absolute error of longitudinal speed

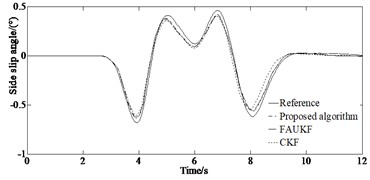
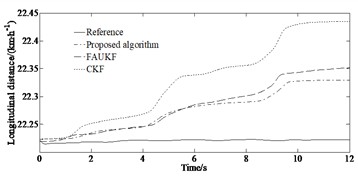
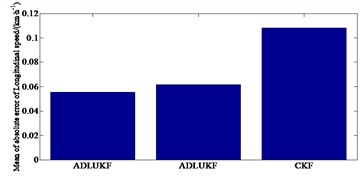
Under the double lane changing road condition, the ADLUKF algorithm can more accurately estimate the yaw rate of the moving vehicle compared to the FAUKF and the CKF algorithm. The yaw rate estimation based on the ADLUKF algorithm is closer to the actual value (Reference value). For the estimation of the side slip angle, both the FAUKF and the CKF algorithm estimator as well as the ADLUKF algorithm estimator can accurately estimate the side slip angle of the vehicle in the first 5 seconds of simulation. After 5 seconds, the estimation effect of the CKF algorithm estimator begins to deteriorate, and its estimation result has a large deviation from the actual side slip angle. However, the tracking effect of the ADLUKF algorithm estimator is still good, and the mean of absolute error of longitudinal speed of the ADLUKF algorithm is the smallest indicating that the ADLUKF algorithm estimator is more accurate than the FAUKF and the CKF algorithm estimator with higher accuracy and better stability.

The computation cost is shown in Tables 1. From Tables 1 it can be seen that the ADLUKF algorithm does not have too high computation cost.

Table 1Comparison of the computation cost under the double lane changing condition

Algorithms	Total times(s)
CKF	6.316
FAUKF	6.346
ADLUKF	6.381

4.1.2. Serpentine condition

Figs. 5(a)-(d) show the simulation results under the serpentine condition. And the common path tracking methods (FAUKF and CKF) are used to compared with the proposed algorithm.

From Fig. 5(a) it can be seen that under the serpentine condition, compared to the FAUKF and the CKF algorithm, the ADLUKF algorithm can more accurately estimate the yaw rate of the moving vehicle. The yaw rate estimation based on the ADLUKF algorithm is closer to the actual value (Reference value). From Fig. 5(b) it can be seen that for the estimation of the side slip angle, both the FAUKF and the CKF algorithm estimator as well as the ADLUKF algorithm estimator can accurately estimate the side slip angle of the vehicle in the first 6 seconds of simulation. 6 seconds later, the estimation effect of the FAUKF and the CKF algorithm estimator begins to deteriorate. Fig. 5(c) indicates that when estimating the longitudinal speed, the CKF algorithm has higher estimation error than that of the ADLUKF algorithm. At the same time it can be seen from Fig. 5(d), the tracking effect of the ADLUKF algorithm estimator is still good, and the mean of absolute error of longitudinal speed of the ADLUKF algorithm is the smallest indicating that the ADLUKF algorithm estimator is more accurate than the FAUKF and the CKF algorithm estimator with higher accuracy and better stability.

Fig. 5Simulation results under serpentine condition

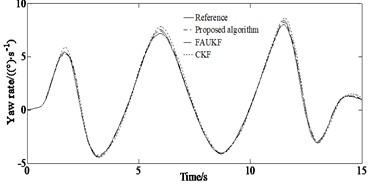
a) Yaw rate

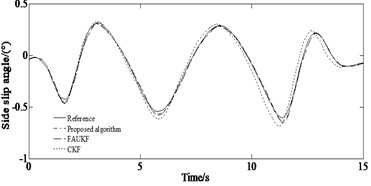
b) Side slip angle

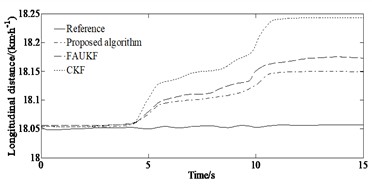
c) Longitudinal speed

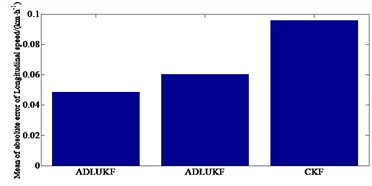
d) Mean of absolute error of longitudinal speed

The mean absolute error (MAE) and root mean square error (RMSE) are considered to verify the estimation accuracy of the proposed algorithm.

From Table 2, it can be seen more intuitively that the estimation accuracy of the ADLUKF algorithm is significantly higher than that of the FAUKF and the CKF method.

Table 2MAE and RMSE indicators of two algorithms

Evaluation index	State value	CKF	FAUKF	ADLUKF
MAE	$u$ (m/s)	0.311	0.158	0.139
	$v$ (m/s)	0.187	0.0563	0.0452
	$ω_{r}$ (rad/s)	0.312	0.0198	0.0163
RMSE	$u$ (m/s)	0.338	0.243	0.126
	$v$ (m/s)	0.249	0.0621	0.0502
	$ω_{r}$ (rad/s)	0.412	0.0301	0.0206

Table 3Analysis of estimation errors of states under different initial conditions of measurement noise covariance matrix

Side slip angle		Initial value of $R$
Side slip angle		eye(3)×0.01	eye(3)×2
RMSE	ADLUKF	0.001	0.003
RMSE	CKF	0.002	0.082

Table 3 is the RMSE of the estimation parameter (Side slip angle) of two algorithms under different initial values of the covariance matrix of measurement noise.

Table 3 shows that CKF is very sensitive to the initial value of the covariance matrix of measurement noise, which is also the reason why it is difficult to ensure the estimation accuracy of CKF in practical applications. The ADLUKF method has significant advantages in estimation accuracy.

The standard deviation (SD) is used to access estimator variability.

From Table 4 it can be seen that compared with the CKF and the FAUKF, the dataset obtained by the ADLUKF has a lower degree of dispersion.

Table 4SD indicator of two algorithms

Evaluation index	State value	CKF	FAUKF	ADLUKF
SD	$u$ (m/s)	0.0704	0.0524	0.0372
	$β$ (deg)	0.2752	0.2486	0.2383
	$ω_{r}$ (rad/s)	3.3763	3.3668	3.3534

4.2. Experimental verification

A real vehicle test is conducted to verify the effectiveness of the algorithm. The real experiment vehicle shown in Fig. 6[26] and the experiment equipment’s are shown in Fig. 7 [26].

Fig. 6Real test vehicle

Fig. 7Measurement equipment’s

The experimental vehicle is a Volkswagen Santana vehicle. The gyroscope is installed at the center of mass of the experimental vehicle, which can meet the measurement requirements for the lateral/longitudinal acceleration, side slip angle and yaw rate of the driving vehicle. The Am-2800 vehicle comprehensive performance test system is used for collecting data. The steering torque/angle tester is used for measuring the steering angle. By measuring the steering wheel angle, the front wheel angle of the experimental vehicle is indirectly measured through the angular transmission ratio between the steering wheel and the front wheels. Driving the test vehicle around the site and the data with a sampling period of 0.01 s is recorded. The collected data is input into the Matlab/Simulink software for offline algorithm evaluation. A block diagram of real vehicle test system is shown in Fig. 8. The experiment is conducted on a dry road surface with a wind speed of less than 3 m/s.

Fig. 8Block diagram of test system

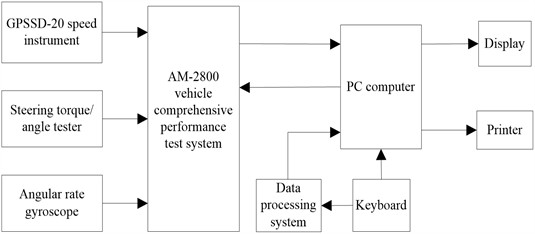
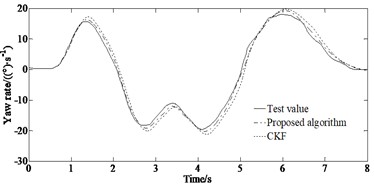
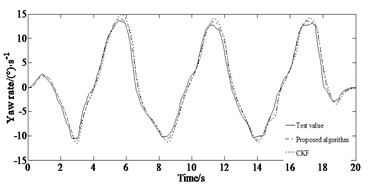
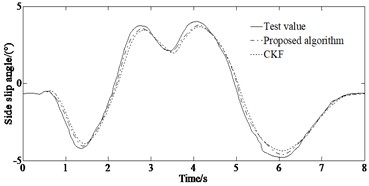
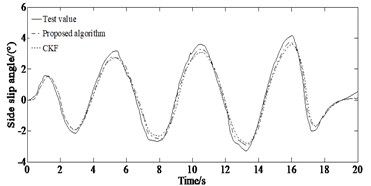
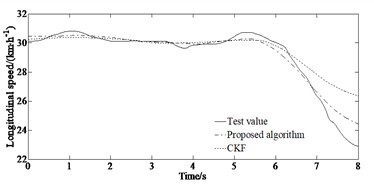
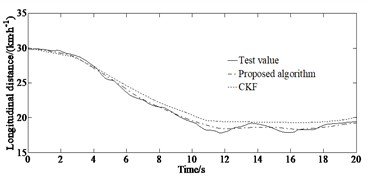
Fig. 9Comparison of the estimated and test values: a) yaw rate under the double lane changing condition; b) side slip angle under the double lane changing condition; c) longitudinal speed under the double lane changing condition; d) yaw rate under the serpentine condition; e) side slip angle under the serpentine condition; f) longitudinal speed under the serpentine condition

Comparison of the estimated and test values: a) yaw rate under the double lane changing condition; b) side slip angle under the double lane changing condition; c) longitudinal speed under the double lane changing condition; d) yaw rate under the serpentine condition; e) side slip angle under the serpentine condition; f) longitudinal speed under the serpentine condition

a)

b)

c)

d)

e)

f)

As shown in Fig. 9 the ADLUKF algorithm is able to estimate the longitudinal speed and side slip angle as well as the yaw rate of the vehicle. Figs. 9(a)-(b) indicates that in the first 2.5 seconds of simulation, the estimators are able to estimate the yaw rate well. However, after 3 seconds, the estimation results based on the CKF algorithm showed distortion, while the ADLUKF algorithm estimator could still reflect the true values of the experiment well. The same result also appeared in the estimation of the side slip angle as shown in Figs. 9(c)-(d). In the first 4 seconds of simulation, the estimators are able to accurately estimate the side slip angle of the vehicle, with the ADLUKF algorithm estimator having higher accuracy. However, after 4 seconds, the CKF algorithm estimator also experienced distortion, possibly due to the non positive definite state covariance matrix, which makes it impossible to find its square root, resulting in incorrect results in Eq. (9). Figs. 9(e)-(f) indicate that both the simulation results of the CKF and the ADLUKF algorithms are consistent with the experimental results verifying the correction of the proposed method for vehicle states estimation. The average error of the ADLUKF algorithm estimator is relatively small. Further verification has shown that the ADLUKF algorithm estimator has better tracking performance and higher accuracy.

5. Conclusions

In order to solve the problem of poor performance of the Unscented Kalman Filter algorithm in estimating vehicle driving state parameters, a dual layer Unscented Kalman Filter algorithm is proposed and integrated with an improved Sage-Husa adaptive filtering algorithm to form an adaptive dual layer Unscented Kalman Filter algorithm estimator. The proposed algorithm can dynamically adjust the process and measurement noise of the system, solving the problem of uncertain system noise. By establishing a nonlinear 3-DOF vehicle estimation model a joint simulation in Carsim and Matlab/Simulink is conducted. In addition, real vehicle experiments are conducted to collect data, and the algorithms are evaluated in Matlab/Simulink software. The estimation results of ADLUKF algorithm and CKF algorithm estimator are compared and analyzed. The results indicate that the ADLUKF algorithm is more accurate and effective in estimating the state parameters of vehicle with higher accuracy and anti-interference ability. There is the issue of potentially non-positive definite covariance matrices. The eigenvalues of a non positive definite covariance matrix contain negative values. By correcting these negative eigenvalues to a small positive value, the covariance matrix is reconstructed based on the eigenvalues and eigenvectors. At the same time, adding regularization terms to the estimation of covariance matrix or adopting a robust model may solve the problem. And the proposed algorithm which is an objective of future research, can be considered for application in other fields, such as indirect bridge structural health monitoring.

References

Y. Liu, D. Cui, and W. Peng, “Optimum control for path tracking problem of vehicle handling inverse dynamics,” Sensors, Vol. 23, No. 15, p. 6673, Jul. 2023, https://doi.org/10.3390/s23156673

Publisher
Y. Liu, D. Cui, and W. Peng, “Optimal lane changing problem of vehicle handling inverse dynamics based on mesh refinement method,” IEEE Access, Vol. 11, pp. 115617–115626, Jan. 2023, https://doi.org/10.1109/access.2023.3324422

Publisher
Y. Liu and D. Cui, “Vehicle dynamics prediction via adaptive robust unscented particle filter,” Advances in Mechanical Engineering, Vol. 15, No. 5, p. 168781322311707, May 2023, https://doi.org/10.1177/16878132231170766

Publisher
G. Li et al., “Vehicle state estimation based on improved Sage-Husa adaptive extend Kalman filtering,” (in Chinese), Automotive Engineering, Vol. 37, No. 12, pp. 1426–1432, 2015, https://doi.org/10.19562/j.chinasae.qcgc.2015.12.012

Publisher
Z. P. Wang, X. Xue, and Y. C. Wang, “State parameter estimation of distributed drive elective vehicle based on adaptive unscented Kalman filter,” (in Chinese), Transaction of Beijing Institute of Technology, Vol. 38, No. 7, pp. 698–702, 2018, https://doi.org/10.15918/j.tbit1001-0645.2018.07.006

Publisher
G. Li, Y. Wang, and C. F. Zong, “Driving state estimation of electric vehicle with four-wheel-hub-motors,” (in Chinese), Automotive Engineering, Vol. 40, No. 2, pp. 150–155, 2018, https://doi.org/10.19562/j.chinasae.qcgc.2018.02.005

Publisher
A. M. Ribeiro, A. Moutinho, A. R. Fioravanti, and E. C. de Paiva, “Estimation of tire-road friction for road vehicles: a time delay neural network approach,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 42, No. 1, pp. 1007–1025, Nov. 2019, https://doi.org/10.1007/s40430-019-2079-y

Publisher
D. J. Kim, J. S. Kim, S.-H. Lee, and C. C. Chung, “A comparative study of estimating road surface condition using support vector machine and deep neural network,” in IEEE Intelligent Transportation Systems Conference – ITSC, pp. 1066–1071, Oct. 2019, https://doi.org/10.1109/itsc.2019.8916965

Publisher
E. Šabanovič, V. Žuraulis, O. Prentkovskis, and V. Skrickij, “Identification of road-surface type using deep neural networks for friction coefficient estimation,” Sensors, Vol. 20, No. 3, p. 612, Jan. 2020, https://doi.org/10.3390/s20030612

Publisher
B.-F. Wu, P.-J. Chang, Y.-S. Chen, and C.-W. Huang, “An intelligent wheelchair anti-lock braking system design with friction coefficient estimation,” IEEE Access, Vol. 6, pp. 73686–73701, Jan. 2018, https://doi.org/10.1109/access.2018.2884658

Publisher
K. Enisz, I. Szalay, G. Kohlrusz, and D. Fodor, “Tyre-road friction coefficient estimation based on the discrete-time extended Kalman filter,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol. 229, No. 9, pp. 1158–1168, Nov. 2014, https://doi.org/10.1177/0954407014556115

Publisher
G. Li et al., “Estimation of vehicle state and road adhesion coefficient based on Kalman filter,” (in Chinese), Journal of South China University of Technology: Natural Science Edition, Vol. 42, No. 8, pp. 129–135, 2014, https://doi.org/10.3969/j.issn.1000-565x.2014.08.020

Publisher
Y.-H. Liu, T. Li, Y.-Y. Yang, X.-W. Ji, and J. Wu, “Estimation of tire-road friction coefficient based on combined APF-IEKF and iteration algorithm,” Mechanical Systems and Signal Processing, Vol. 88, pp. 25–35, May 2017, https://doi.org/10.1016/j.ymssp.2016.07.024

Publisher
C. Wang, C. Song, and J. Li, “A federated filter design of electronic stability control for electric-wheel vehicle,” in 8th International Congress on Image and Signal Processing (CISP), pp. 1105–1110, Oct. 2015, https://doi.org/10.1109/cisp.2015.7408045

Publisher
X. Fu et al., “Estimation of road adhesion coefficient based on fading memory unscented Kalman filtering with exponential weighting,” (in Chinese), Automobile Technology, No. 1, pp. 31–37, 2018, https://doi.org/10.19620/j.cnki.1000-3703.20170512

Publisher
Q. Zhu, J. Zhang, L. Zhou, and Z. Zhao, “Vehicle speed estimation in driving case based on distributed self-adaptive unscented Kalman filter for 4WD hybrid electric car,” Scientia Sinica Technologica, Vol. 46, No. 5, pp. 481–492, May 2016, https://doi.org/10.1360/n092015-00240

Publisher
B. L. Boada, M. J. L. Boada, and V. Diaz, “Vehicle sideslip angle measurement based on sensor data fusion using an integrated ANFIS and an unscented Kalman filter algorithm,” Mechanical Systems and Signal Processing, Vol. 72-73, pp. 832–845, May 2016, https://doi.org/10.1016/j.ymssp.2015.11.003

Publisher
E. Massarelli, M. Raimondi, and S. Mara, “Output-only modal analysis and system identification for indirect bridge health monitoring: needs, requirements, and limitations,” in IOMAC 2024, LNCE 515, Vol. 515, pp. 505–515, 2024.

Publisher
M. Dalmasso, M. Civera, and V. de Biagi, “Gaussian process regression (GPR)-based missing data imputation and its uses for bridge structural health monitoring,” Advances in Bridge Engineering, Vol. 6, No. 23, pp. 1–21, 2025.

Publisher
M. Aimar, M. Civera, S. Foti, and B. Chiaia, “Preliminary insights from surveys of bridges at high scouring risk in west piedmont,” Procedia Structural Integrity, Vol. 62, pp. 609–616, Jan. 2024, https://doi.org/10.1016/j.prostr.2024.09.085

Publisher
Y. Liu, D. Cui, and W. Peng, “Vehicle state and parameter estimation based on improved extend Kalman filter,” Journal of Measurements in Engineering, Vol. 11, No. 4, pp. 496–508, Dec. 2023, https://doi.org/10.21595/jme.2023.23475

Publisher
C. M. Liu, Z. B. Peng, and X. J. Wu, “Joint estimation of vehicle motion state based on adaptive fuzzy extended Kalman filter,” (in Chinese), Automobile Technology, Vol. 559, No. 4, pp. 23–30, 2022, https://doi.org/10.19620/j.cnki.1000-3703.20210263

Publisher
X. Wang, A. Wang, D. Wang, Y. Xiong, B. Liang, and Y. Qi, “A modified Sage-Husa adaptive Kalman filter for state estimation of electric vehicle servo control system,” Energy Reports, Vol. 8, pp. 20–27, Aug. 2022, https://doi.org/10.1016/j.egyr.2022.02.105

Publisher
J. L. Xu and G. J. Zhang, “Vehicle state estimation based on adaptive double-layer untracked Kalman filter,” Journal of Chongqing University of Technology, Vol. 38, No. 13, pp. 29–36, 2024, https://doi.org/10.3969/j.issn.1674-8425(z).2024.07.004

Publisher
S. G. Sun and Q. X. Wen, “The application of improved Sage-Husa algorithm in aircraft integrated navigation,” (in Chinese), GNSS World of China, Vol. 46, No. 3, pp. 54–60, 2021, https://doi.org/10.12265/j.gnss.2021012401

Publisher
Y. Liu and D. Cui, “Estimation of vehicle state based on maximum correntropy square-root cubature Kalman Filter,” Journal of Measurements in Engineering, Vol. 13, No. 1, pp. 152–167, Mar. 2025, https://doi.org/10.21595/jme.2024.24376

Publisher

About this article

Received

April 23, 2025

Accepted

January 8, 2026

Published

February 6, 2026

DOI

https://doi.org/10.21595/jme.2026.25025

Keywords

vehicle state estimation

adaptive double-layer UKF

Sage-Husa

Acknowledgements

This research was supported by the Open Research Program of Huzhou Key Laboratory of Urban Multidimensional Perception and Intelligent Computing under Grant No. UMPIC202404. This research was supported by the Science and Technology Program Foundation of Weifang under Grant 2023GX003. At the same, this research was financially supported by the Open Research Fund from the State Key Laboratory of Rolling and Automation, Northeastern University, under Grant 2021RALKFKT008. The first author gratefully acknowledges the support agency.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Qianqian Wang: simulation techniques. Yingjie Liu: mathematical model. Dawei Cui: spelling and grammar checking as well as software.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Q. Wang, Y. Liu, and D. Cui, “Estimation of vehicle state based on improved dual layer UKF,” Journal of Measurements in Engineering, Vol. 14, No. 2, –14, Feb. 2026, https://doi.org/10.21595/jme.2026.25025

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jme.2026.25025
UR  - https://doi.org/10.21595/jme.2026.25025
TI  - Estimation of vehicle state based on improved dual layer UKF
T2  - Journal of Measurements in Engineering
AU  - Wang, Qianqian
AU  - Liu, Yingjie
AU  - Cui, Dawei
PY  - 2026
DA  - 2026/02/06
PB  - Extrica
VL  - 14
IS  - 2
SN  - 2335-2124
SN  - 2424-4635
ER  - 

Copy Ris

Copied to clipboard!

 @article{Wang_2026, title={Estimation of vehicle state based on improved dual layer UKF}, ISSN={2424-4635}, url={https://doi.org/10.21595/jme.2026.25025}, DOI={10.21595/jme.2026.25025}, journal={Journal of Measurements in Engineering}, publisher={JVE International Ltd.}, author={Wang, Qianqian and Liu, Yingjie and Cui, Dawei}, year={2026}, month=feb }

Copy Bibtex

Copied to clipboard!

[1]Q. Wang, Y. Liu, and D. Cui, “Estimation of vehicle state based on improved dual layer UKF,” Journal of Measurements in Engineering, Feb. 2026, doi: 10.21595/jme.2026.25025.

Copy IEEE

Copied to clipboard!

Wang, Qianqian, Yingjie Liu, and Dawei Cui. “Estimation of Vehicle State Based on Improved Dual Layer UKF.” Journal of Measurements in Engineering, February 6, 2026. https://doi.org/10.21595/jme.2026.25025.

Copy Chicago

Copied to clipboard!

Estimation of vehicle state based on improved dual layer UKF

Abstract

Highlights

1. Introduction

2. Mathematical model of vehicle dynamics

2.1. 3-DOF vehicle model

2.2. Tire model

3. The ADLUKF algorithm

3.1. Standard UKF algorithm

3.2. Dual layer UKF algorithm

3.3. ADLUKF

4. Numerical simulation and experimental verification

4.1. Numerical simulation

4.1.1. Double lane changing condition

4.1.2. Serpentine condition

4.2. Experimental verification

5. Conclusions

References

About this article

Related Articles