Research on chatter monitoring of ultrasonic milling of thin-walled parts based on ICS-CNN network

2.1. Multi-scale feature extraction-inception module

In traditional convolutional neural networks, fixed-size convolution kernels (such as 3×3 or 5×5) are typically used for feature extraction, which may miss important feature information at different scales. The Inception-V1 module, however, simultaneously captures local detail information (via small convolution kernels) and broader semantic information (via large convolution kernels) by parallelly using 1×1, 3×3, and 5×5 convolution kernels along with 3×3 max pooling operations. The 1×1 convolution kernel serves as a dimensionality reduction component in this structure.

Before performing 3×3 and 5×5 convolutions, 1×1 convolutions are first used to reduce the dimensionality of input channels, which minimizes the scale of network parameters and reduces computational complexity. This allows the network to increase both depth and width while avoiding overfitting and computational resource waste caused by excessive parameters. Additionally, this approach enriches the extracted features, which are ultimately fused along the channel dimension and used as input for the next module. This Inception structure broadens the width of each layer and increases network depth without additional computational overhead, thereby enhancing the generalization ability and accuracy of chatter detection.

2.2. Sparse residual connections incorporated into the CBAM mechanism

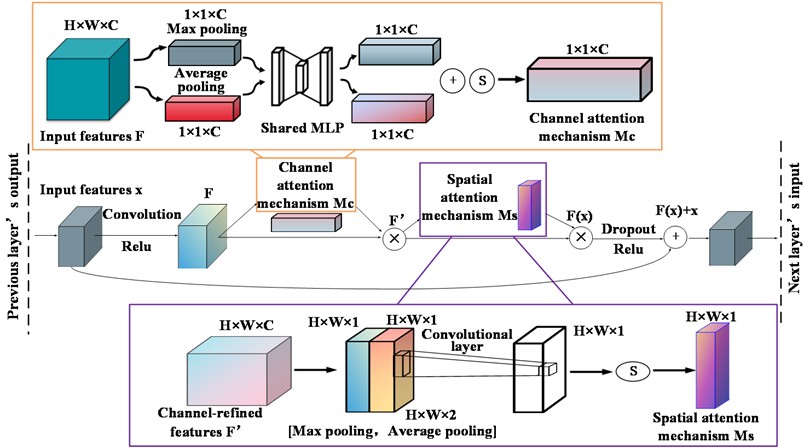
The combination of the CBAM (Convolutional Block Attention Module) [28] and sparse residual connections can enhance the network's ability to focus on key features while reducing computational load and parameter count through sparsity. The CBAM module adjusts feature maps via attention weights, enabling residual blocks to better process important feature information. Sparse residual connections optimize network structure and parameter efficiency while ensuring the trainability of network depth. During training, the introduction of sparsity prompts the network to automatically select important connections, while CBAM guides the network to utilize feature information more effectively on these connections, thereby improving network performance and generalization ability. The network structure is shown in Fig. 1.

Fig. 1Sparse residual links integrated into CBAM mechanism

2.3. FPN multi-scale fusion

The Feature Pyramid Network (FPN) is characterized by its ability to organically integrate features from different scales, thus laying a solid feature foundation for subsequent tasks. The multi-scale features extracted by the Inception module provide richer feature inputs for the FPN. This enables the FPN to fuse more diverse feature information when constructing the feature pyramid, further enhancing the representation ability for targets of different scales. The combination of the Inception’s multi-scale feature extraction and the FPN's feature fusion and pyramid construction allows the model to better handle targets of different sizes. It not only improves computational efficiency but also enhances performance.

3.1. Experimental platform and experimental parameters

The experimental setup used in this study includes a machining center, an ultrasonic vibration assistance system, and a cutting force measurement system, as shown in Fig. 2.

Parameters of TH5650 Vertical Machining Center: Spindle speed range: 50-6000 r/min; Maximum torque: 70/909 (continuous/30 min) N·m; Power: 11/7.5 kW; Travel of $X$, $Y$, $Z$ axes: 850 mm, 500 mm, 630 mm respectively; Maximum feed rate: 24 m/min for $X$ and $Y$ axes; 15 m/min for Z axis.

The TiAlN-coated solid carbide tool MS2SS was chosen for this experiment. At high cutting temperatures, the aluminum element in the coating forms oxides, which improve the tool’s thermal hardness and wear resistance. The main mechanical properties are listed in Table 1.

The MS2SS tool steel used in TiAlN-coated solid carbide cutting tools exhibits brittle behaviour, lacking macroscopic plastic deformation. The stress-strain curve abruptly terminates upon reaching fracture strength, precluding analysis of yield points or necking processes characteristic of ductile materials.

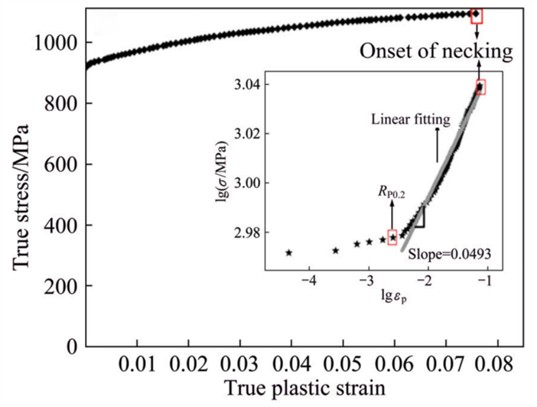
The Fig. 3 depicts the true stress-true plastic strain curve for Ti-6Al-4V material, incorporating dual-logarithmic linear fits for and to systematically analyse the material’s mechanical behaviour and strain hardening patterns during plastic deformation. The main plot demonstrates that true stress increases continuously with rising true plastic strain, indicating the material exhibits pronounced work hardening (strain hardening) characteristics during plastic deformation. That is, as the amount of plastic deformation increases, the material’s resistance to further plastic deformation progressively strengthens. To quantitatively characterise the strain hardening behaviour, a double-logarithmic transformation was applied to the stress-strain relationship during the plastic deformation stage based on the Holman equation, followed by linear fitting. The results reveal a good linear relationship between and , with a fitted slope of 0.0493. This slope represents the material's strain hardening index, whose physical significance lies in the material’s resistance to plastic deformation. A highervalue indicates stronger work hardening capability.

Fig. 2Experimental platform and data acquisition system. The photograph was taken by Guanzhong Wu at the Engineering Training Center of Liaoning Petrochemical University on March 4, 2025

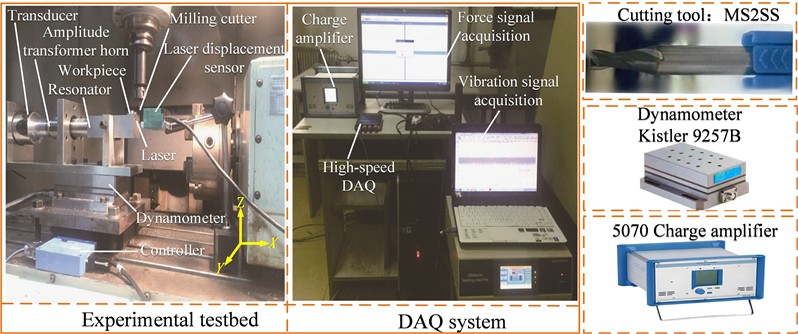
Fig. 3Bipolar logarithmic fitting analysis of true stress-true plastic strain curves and strain hardening characteristics for Ti-6Al-4V

Based on the processing parameters shown in Table 2, the force in the $F_x$, $F_y$, and $F_z$ directions was collected using the Dynoware software.

3.2. Design parameters of the band-stop filter and the signal processing steps

A Band-Stop Filter (BSF) is a frequency-selective device primarily used to suppress or attenuate signals within a specific frequency range while allowing signals outside this range to pass through. To accurately capture signals containing ultrasonic frequencies at 20 kHz, the sampling frequency is chosen as $f_s=$ 50 kHz. Since the goal is to filter out the ultrasonic frequency, the center frequency should be set to the digital frequency corresponding to the ultrasonic frequency. The digital center frequency is set to $W_0=$ 2.513 kHz. Given that the ultrasonic frequency is 20 kHz, the bandwidth is selected as [18 kHz-22 kHz], corresponding to a digital frequency range of [2.2608-2.7632]. This ensures the removal of both the ultrasonic frequency and the surrounding noise interference. The filter order is chosen as $N=$ 4. The relevant formulas are as follows:

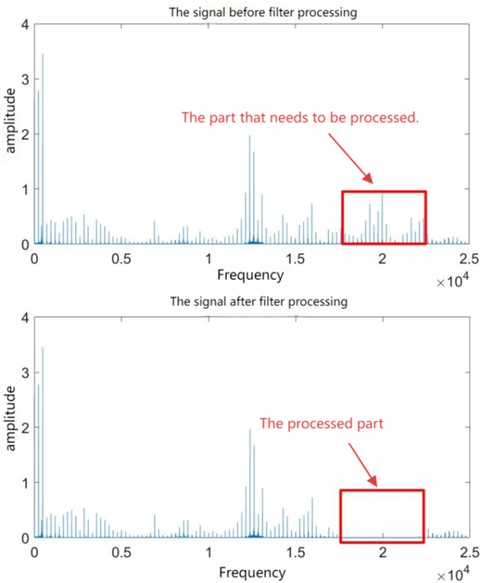
As shown in Fig. 4 Frequency-domain analysis is performed on the filtered data to verify whether the ultrasonic frequency is effectively removed. The filtered data is converted to the frequency domain using FFT again, and whether the amplitude at the ultrasonic frequency position in the spectrum is significantly reduced is observed. Meanwhile, if the ultrasonic frequency component is effectively suppressed, it indicates that the preprocessing of the band-stop filter is successful; otherwise, the filter parameters (such as center frequency, bandwidth, order, etc.) need to be readjusted, and the above steps are repeated until a satisfactory filtering effect is obtained.

3.3. Dataset construction

The data pre-processed by the filter cannot be directly used as the dataset for the neural network. During the data processing, not only should the influence of the ultrasonic frequency be eliminated through the filter, but also FFT analysis should be performed on the data. And the corresponding machining processes, such as idle cutting, chatter, and stable cutting, should be labeled according to different frequencies. Labels are added to the data corresponding to different machining processes, so as to provide training targets for the neural network.

In addition, since there are differences in the amplitude ranges of the data generated by different machining methods, to avoid the influence of these differences on the neural network training, the data needs to be normalized. Through normalization, the distribution range of the data can be adjusted to an appropriate interval.

Fig. 4Band-stop filter processing effect diagram

4.1. Monitor processes

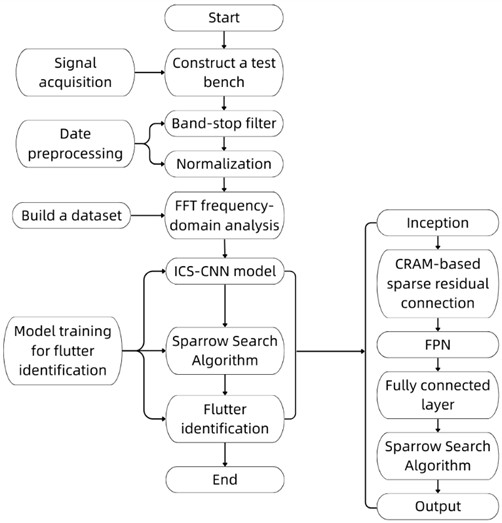
The overall chatter recognition process is shown in Fig. 5, with the specific steps as follows:

1) Acquire force signal data during the milling process.

2) Process the collected force signals using a band-stop filter to eliminate ultrasonic frequencies.

3) Perform frequency-domain analysis on the preprocessed data, convert the one-dimensional force signal data into two-dimensional frequency-domain images through FFT transformation and normalization, and label the data with category labels. Divide the converted frequency-domain image data into training, testing, and validation sets as input data for subsequent convolution operations.

4) Input the two-dimensional frequency-domain images into the ICS-CNN model to automatically extract chatter-related features through Inception multi-scale feature extraction, sparse residual connections integrated with CBAM, and FPN.

5) Use the Sparrow Optimization Algorithm (SSA) to find the optimal solution for the ICS-CNN model’s objective function and obtain the training result output.

6) For the trained model, import data into the trained ICS-CNN monitoring model to directly classify the machining states.

Fig. 5ICS-CNN chatter monitoring process based on sparrow optimization algorithm

4.2. Optimization of hyperparameters by the Sparrow optimization algorithm

After constructing the neural network structure for chatter identification, the Sparrow Optimization Algorithm (SSA) is used to optimize hyperparameters. The fixed hyperparameters in this paper are: AdamW optimizer, Label Smoothing loss function, ReLU activation function, and a Dropout regularization coefficient of 0.5.

AdamW adds weight decay to Adam, which can balance the efficiency of gradient update and the regularization effect: it not only accelerates the parameter update of the ICS-CNN convolution layer through adaptive learning rate, and quickly reduces the loss, but also can suppress overfitting, reduce the model’s dependence on specific working condition noise features, and improve generalization ability. Loss function: Label Smoothing addresses the “over-confident” issue of one-hot labels by setting the positive sample labels to $1-\epsilon$ ($\epsilon =$0.1) and the negative sample labels toε.The formula for the loss function is as follows:

This retains the model's ability to learn uncertainty, avoids overfitting to noisy samples, enhances the sensitivity of recognizing early fluttering weak features, and reduces classification errors. The ReLU activation function can prevent the gradient disappearance in deep networks and ensure the effective transmission of frequency-domain features of ICS-CNN; moreover, it is computationally simple, has no gradient saturation in the positive range, and can quickly distinguish the sensitive and non-sensitive frequency band features of the vibration-sensitive signals in the spectrogram. Regularization coefficient: Dropout = 0.5. During training, 50 % of the neurons in the fully connected layers are randomly deactivated, which can prevent overfitting (avoiding redundant features such as noise in the learning device); through pre-experiment verification, this coefficient can balance feature retention and robustness, making the model's accuracy on the validation set fluctuate the least and having the best anti-noise ability.

The optimization ranges are: learning rate [0.0001, 0.01], batch size [16, 64], and weight magnitude [0.001, 0.1]. The optimization results are: learning rate of 0.0026, batch size of 32, and weight magnitude of 0.057.

5.1. Test results

During the research, the Sparrow Optimization Algorithm (SSA) was applied to successfully locate the optimal solution, and the relevant parameters were fed back to the ICS-CNN model. The number of iterations was reasonably increased to 200. Finally, the loss function curve and accuracy curve were successfully obtained, and their detailed information is shown in Fig. 6.

Fig. 6Loss function curve and accuracy curve for 200 iterations

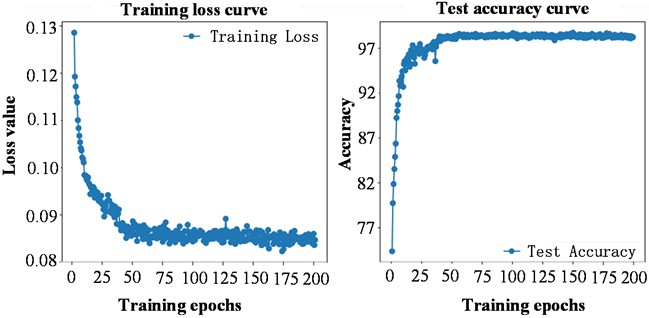
It can be seen that the loss function continuously converges until it approaches a steady state. Notably, although the loss function converges continuously, it does not ultimately converge to zero, which precisely indicates that the model exhibits good performance on the training set and effectively avoids the risk of overfitting. From the accuracy curve, it is clearly observed that the accuracy climbs extremely rapidly in the initial stage, then gradually stabilizes, and finally reaches a high accuracy of 98.37 %. This result strongly confirms that the model also performs excellently on the test set, achieving high accuracy while successfully eliminating overfitting. Comprehensive analysis above fully demonstrates the outstanding effect of the ICS-CNN model based on the Sparrow Optimization Algorithm in chatter identification for ultrasonic milling.

5.2. Visual analysis of the model

To clearly and intuitively understand the performance of the model on the training set and the test set, it is necessary to conduct a visual analysis of the model. Visualization methods can not only help further verify the effectiveness of the model but also evaluate the model’s performance in an intuitive way. In this paper, two visualization approaches, namely the T-SNE visualization scatter plot and the decision boundary plot, are used to conduct a more in – depth verification and evaluation of the model, providing multiple perspectives for the analysis of the model’s performance, as shown in Fig. 7 and Fig. 8.

First, the visualization results of the model on the training set (left plot) were observed through T-SNE scatter plots. The results clearly show that the data form three distinct clusters, with clear boundaries between clusters and no confusion between samples of different clusters. This phenomenon fully demonstrates the model's excellent classification ability on the training set.

Fig. 7T-SNE visual scatter plot

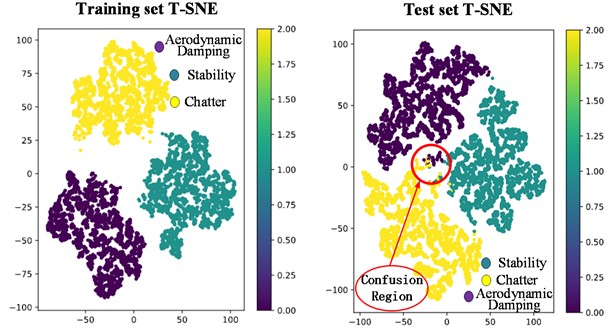
Meanwhile, observing the model's performance on the test set (right plot), the three clusters are nearly completely separated, with only a few samples confused, concentrated in the areas marked by red circles in the figure. This result further highlights the model's excellent performance during the testing phase and strongly proves its good applicability and reliability in practical application scenarios.

Using only one verification method to measure the model's performance is insufficient. To rigorously demonstrate the model’s performance, this paper uses decision boundary plots to visualize the training and testing effects, providing supplementary evidence for the model's performance, as shown in Fig. 8.

Fig. 8Decision boundary diagram

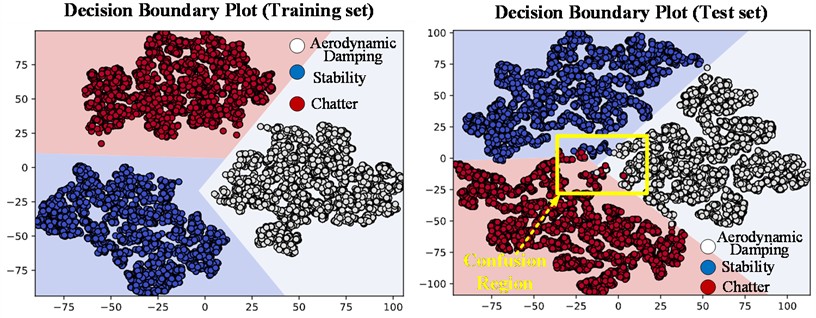
By observing the model's performance on the training set (left plot) in the decision boundary diagram, it can be clearly seen that the three clusters are accurately and perfectly classified without any confusion. This result is highly consistent with the conclusion drawn from the T-SNE analysis of the training set, further verifying the model's excellent classification ability during the training phase. Meanwhile, observing the model's performance on the test set (right plot), it is evident that the three clusters are almost completely separated, with only a minimal number of samples confused. These confused samples are concentrated in the areas marked by yellow boxes in the figure, fully demonstrating the model's superior performance during the testing phase.

Through the synchronous analysis of T-SNE and decision boundary diagrams, the results of the two visualization methods corroborate each other, providing strong evidence for the model's good applicability and reliability in practical application scenarios. This significantly enhances the credibility and persuasiveness of the model evaluation conclusions.

5.3. Comparative experiments on chatter identification effects of different models

To verify the effectiveness of the proposed method, this study conducted a detailed comparative analysis. Focusing on the identification performance of network models, the Sparrow Optimization Algorithm (SSA) was combined with four common network models to construct the SSA-CNN (Convolutional Neural Network with SSA), SSA-ResNet (Residual Neural Network with SSA), SSA-SVM (Support Vector Machine with SSA), and SSA-Inception-V1 (Inception-V1 with SSA). These combined models were then comprehensively compared with the proposed model (SSA-ICS-CNN). Through visual analysis of different models, the performance of each model was accurately evaluated to validate the effectiveness of the proposed method, as detailed in Fig. 9.

Fig. 9Visual comparison of different models

By carefully observing Fig. 9, it is evident that the proposed SSA-ICS-CNN model outperforms other models on the test set. In its test results, the proportion of confused samples is extremely small, whereas other models exhibit significantly higher confusion rates on the test set. Further comparison of accuracy data for different methods in Table 3 shows that the SSA-ICS-CNN model achieves the highest accuracy among all compared models, which strongly reinforces its significant performance advantages and ideal effectiveness.

In addition to model comparisons, different optimization algorithms are also contrasted, including the Random Search-optimized model (RS-ICS-CNN), Simulated Annealing-optimized model (SA-ICS-CNN), Tree-structured Parzen Estimator-optimized model (TPE-ICS-CNN), Covariance Matrix Adaptation Evolution Strategy-optimized model (CMA-ES-ICS-CNN), Genetic Algorithm-optimized model (GA-ICS-CNN), and Particle Swarm Optimization-optimized model (PSO-ICS-CNN). The experimental settings are listed in Table 4.

Fig. 10The ROC curve is used to represent the performance of various models

For generating ROC curves of various models to quantify and compare the classification performance of the SSA-ICS-CNN model with the other six models (RS-ICS-CNN, SA-ICS-CNN, TPE-ICS-CNN, CMA-ES-ICS-CNN, GA-ICS-CNN, PSO-ICS-CNN), first, regarding the task and sample set determination, aiming at the three-category task of distinguishing idle cutting, stable cutting, and chatter states, the “One-vs-Rest” strategy is adopted to convert it into a binary classification task, and the preprocessed test set (divided in a 7:1:2 ratio for training, validation, and testing) is selected as the evaluation sample source. Next, for obtaining predictive probabilities, the probability vectors from the fully connected layer of each of the seven models are extracted, and in each “One-vs-Rest” scenario, the probability of the target category is taken as the “positive class score” while the maximum probability of the other two categories is taken as the “negative class score”. Then, for calculating TPR and FPR, 101 thresholds ranging from 0 to 1 with an interval of 0.01 are set; samples are classified according to these thresholds, the numbers of TP (True Positives), FP (False Positives), TN (True Negatives), and FN (False Negatives) are counted under each threshold, and TPR, and FPR are further computed. Finally, for plotting curves and calculating AUC, each model generates 3 sub-ROC curves, the AUC of each sub-ROC curve is calculated using the trapezoidal integration method and the average of these three AUC values is taken as the final AUC of the model; the average ROC curves of the seven models are plotted in the same coordinate system. Fig. 10 shows the ROC curves of seven algorithms (the closer the ROC curve is to the upper-left corner, the higher the classification accuracy of the model; AUC is the area under the ROC curve, and a larger AUC indicates better classification performance of the model). It can be seen from the figure that the proposed identification model has the highest classification accuracy, with an AUC of 0.983, which is larger than that of the other six identification models. This indicates that the model not only has the best classification performance but also faster convergence ability and higher convergence accuracy:

Fig. 11The identification accuracy and discrimination time of different models

The results of this study demonstrate that the proposed SSA-ICS-CNN model exhibits outstanding overall performance in identifying chatter during ultrasonic milling of thin-walled components. As depicted in Fig. 11 and Table 5, this model achieves optimal values in recognition accuracy (98.37 %), Matthews correlation coefficient (0.9327), and F1 score (0.9717), whilst requiring only 147 milliseconds for classification. This represents a significant improvement over other comparative models. This outstanding performance stems from the SSA algorithm's exceptional global search capability during hyperparameter optimisation, effectively circumventing local optima. Concurrently, the multi-scale feature fusion mechanism (Inception module) introduced within the ICS-CNN architecture, attention-guided (CBAM) and feature pyramid network (FPN) mechanisms within the ICS-CNN architecture enhance frequency-domain feature extraction. The sparse residual structure substantially reduces computational complexity while preserving expressive power, thereby unifying high accuracy with high real-time performance. Compared with recent related studies, this approach demonstrates distinct technical advantages, further reducing response time while maintaining comparable accuracy. These comparisons indicate that SSA-ICS-CNN not only outperforms existing mainstream intelligent chatter monitoring methods in performance metrics but also provides a genuinely practical solution meeting industrial online monitoring requirements.

From an industrial application perspective, the developed recognition system possesses the potential for integration into CNC machine tool control units, enabling real-time chatter monitoring and predictive maintenance. Capable of completing state discrimination within 147 milliseconds, the system provides critical technical support for timely adjustment of cutting parameters, thereby preventing workpiece damage and tool wear. Its favourable computational efficiency renders it suitable for edge computing environments, aligning with the evolving trend of end-edge-cloud collaborative architectures within contemporary intelligent manufacturing systems.

Nevertheless, this research retains certain limitations. The current model was trained and validated under specific machining conditions and using a limited-scale dataset; its generalisability across broader operating conditions requires further validation. Furthermore, while the model demonstrates favourable computational efficiency, its deployability on resource-constrained embedded devices requires further optimisation through model compression techniques. Future research will focus on constructing multi-condition datasets, designing adaptive lightweight networks, and achieving closed-loop integration with actual CNC systems to advance the method's widespread adoption in industrial settings.