Modal analysis of the human head-neck mathematical model

1. Introduction

The human head, when subjected to mechanical vibration either by contact with vibrating structures or by action of an acoustic field, responds by vibrating in certain modes with an intensity of depending on its own structural or anatomical peculiarities [1]. Investigation and explanation of its responses are problems in their own, and the knowledge of how and why it vibrates will contribute to a general understanding of human body mechanics. This may aid in development of “a new medical instrument for early diagnosis of brain diseases” [2] or a protective headgear in both civilian and military contexts.

Earlier research on human head vibration was mainly based on experimental tests involving animals, cadavers and volunteer living subjects. V. Bekesy [3] investigated the vibration response of a cadaver skull in an acoustic field and reported that the first resonant frequency of the skull to be 1800 Hz. Both Hodgson et al. [4] and Gurdjian et al. [5] reported that the resonant frequency of a cadaver head in their mechanical impedance analysis was approximately 300 Hz. At the same time, Stalnaker and Fogle [6] utilized an electromagnetic shaker in their experimental tests of a fresh unembalmed cadaver head and determined that the resonant frequencies were 166 and 820 Hz. Khalil et al. [7] conducted an experimental study on two cadaver heads (one male and one female) using an impact hammer. The respective fundamental frequencies found were 1385 Hz and 1641 Hz. In contrast, experimental studies on living human subjects showed the resonant frequency arranged from a few Hz to 300 Hz [3, 5, 8-10]. Despite the bulk of valuable information provided by experimental data, these tests do not only raise issues in morality and ethics, but also induce many research concerns such as limited flexibility in experimental data due to scarce subjects and non-standardized experimental procedures. Moreover, results from experiments may vary with the individual subject and thus may show a lack of reproducibility as well as reliability.

These earlier FE studies had undoubtedly provided some insights in the dynamic characteristics of the human head. Nonetheless, they had made numerous approximations and simplifications in the geometry of the head. In the present work, a detailed FE model of human head and neck, which includes the facial and intracranial details such as the subarachnoid space, has been developed and its modal responses have been determined. In addition, the simulated modal responses in terms of resonant frequencies and mode shapes are compared with those in literature, unlike most previous studies which only compared their resonant frequencies and ignored modal validation in terms of mode shapes. Moreover, this paper also investigates the effect of damping on dynamic characteristics, with the introduction of damping factors in the complex eigenvalue analysis.

2. Methods and materials

In order to determining modal responses, modal analysis using FEM is performed using an implicit software Abaqus v6.10. In this present study, three global material damping factors of 0.1, 0.2 and 0.4, which are within the range of damping factors of head and neck found in the literature [7, 9, 10], are included in this complex eigenvalue analysis of the multi-degree of freedom problem. In addition, the biomechanical parameters such as intracranial pressure (ICP) and skull stresses are evaluated at each individual mode for both undamped and damped cases.

The surface nodes at the base of the head-neck model are constrained in all the six degrees of freedom (Fig. 1) while all the interfaces between components are prescribed with tie conditions since interaction properties, such as general contact and sliding, are not available in modal analyses.

Fig. 1Fixed boundary condition is applied at the surface nodes of the base of the neck

3. Results

This section presents result on the dynamic characteristics (resonant frequencies and mode shapes) of the 3D FE model of human head-neck. By performing modal analysis on the 3D FE head-neck system using the Abaqus implicit code, twenty-five resonant frequencies and associated mode shapes are recognized in the frequency band of 35 to 360 Hz (Fig. 2). These computed resonant frequencies in the undamped and damped free vibrations are tabulated, with their respective first resonant frequencies at 35.57 Hz, 34.59 Hz, 34.43 Hz and 33.78 Hz. Additionally, there is a slight variation in the resonant frequencies between both the undamped and damped free vibration scenarios. Within the twenty-five mode shapes, Fig. 3 (which are movie still instances) shows five various, distinguishable mode shapes of the head-neck complex: an anterior-posterior extension-flexion mode of the head about the neck at 35.57 Hz, a lateral flexion mode at 62.89 Hz, an axial rotational mode of the head about its vertical axis at 72.40 Hz, a S-shaped anterior-posterior retraction mode of the head and neck at 221.51 Hz and finally a vertical translational mode of the head at 254.04 Hz. Also, the lateral flexion of the nasal lateral cartilages as well as the lateral translation of the mandible or “mastication” mode, which dominate after the primary modes of the head-neck structure within its first twenty-five modes, are identified (Fig. 3). The mode shapes for the damped vibration cases are identical to that of the undamped vibration, except for the difference in the arbitrary magnitude of biomechanical parameters such as displacement, ICP as well as skull Mises stresses.

Fig. 2Mid-sagittal view of the displacement magnitude (in mm) contour plots of the head-neck model, showing various mode shapes and their corresponding frequencies for the undamped vibration case

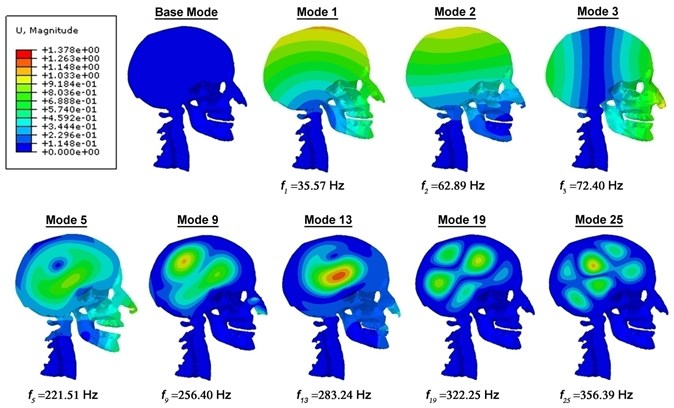
Fig. 3Comparison of the mode shapes with Meyer et al. [11]’s FE head-neck model

4. Discussion

5. Conclusions

1) The knowledge of how and why the modal responses of the human head change is very important in the study of head injury. This study employs both the traditional and the complex modal analyses of a detailed finite element (FE) model of human head-neck system. It is conducted with the goal of determining modal responses in terms of resonant frequencies and mode shapes as well as finding an explanation for huge variation in head’s resonant frequencies reported in literature.

2) Unlike most of the previous studies, this study compares both modal responses without ignoring modal validation in terms of mode shapes. These results are found to be within a reasonable range reported in literature. It is found that increasing displacement contour loops in the brain for higher frequency modes probably exhibit the shearing and twisting modes of the brain. Additional and rarely reported modal responses such as “mastication” mode of the mandible and flipping mode of nasal lateral cartilages are identified and this may bring interest to clinicians or surgeons who are specialized in rhinoplasty or temporomandibular joint disorder. This suggests a need for detailed modeling to identify all the additional frequencies of each individual part.

3) The current study also investigates the effects of damping on both modal responses and biomechanical responses. It is found that a damping factor of above 0.2 has an amplifying effect in reducing higher mode frequencies, whilst diminishing effect in lowering peak biomechanical responses, indicating the importance of identifying the appropriate optimized damping factor.