An availability model based on a three-stage failure process under age based replacement

Yang, Ruifeng; Kang, Jianshe; Zhang, Xinghui; Li, Haiping

Vibroengineering Procedia

Browse Procedia

Published: 03 November 2014

Check for updates

An availability model based on a three-stage failure process under age based replacement

Ruifeng Yang¹

Jianshe Kang²

Xinghui Zhang³

Haiping Li⁴

^{1, 2, 3, 4}Mechanical Engineering College, Shijiazhuang, China

Corresponding Author:

Ruifeng Yang

Cite the article Download PDF

Downloads 1317

Abstract

This paper proposes a joint optimal policy of inspection and age based replacement based on a three-stage failure process to jointly optimize the inspection and replacement intervals. The three-stage failure process divides the failure process of system into three stages: namely normal, minor defective and severe defective. When the minor defective stage is identified, the subsequent inspection interval is halved. Once identifying the severe defective stage, the maintenance action is carried out immediately. The system is replaced once it reaches the certain age. Finally, a numerical example is presented to demonstrate the efficiency of the proposed model.

1. Introduction

Nowadays CBM attracts more interest because of the efficiency of deriving the actual operating information by inspection which can help managers make scientific maintenance decisions. In industry, maintenance operators often inspect the system using the hand-held inspection tools with a planned interval. However, the determination of inspection interval is one of the key issues [1]. The delay-time concept, which assumes the state of the system before failure to be either normal or defective, has the obvious advantage for optimizing the inspection intervals because it can capture the relationship between the inspection interval and the number of failures [2].

However, the state of system may by described more than two before failure as the three color scheme is mostly used to divide the state before failure into green (normal), yellow (need attention), and red (need immediate attention) [3]. Therefore, Wang firstly extended the two-stage delay time to a three-stage failure process, where the traditional delay time stage is further divided into two stages: minor defective stage and severe defective stage [4]. Finally a case study is given to show that delaying maintenance at the minor defective stage is better than maintenance immediately. A preventive maintenance model with a two level inspection policy based on a three stage failure process is proposed by Wang et al. [5]. But as one of the most commonly used preventive maintenance and replacement policies, age based replacement policy is not considered in [4, 5]. According to age based replacement policy, the system is replaced upon failure or at fixed age, whichever occurs first [6, 7]. The joint policy of regular inspections and age based preventive replacement has been widely used in industrial applications, but joint optimization for inspection and replacement intervals based on the three-stage failure process has not been developed.

In this paper, a joint optimal policy of inspection and age based replacement based on a three-stage failure process is introduced. The system is replaced once it fails or reaches the certain age. When the severe defective stage is identified, repair will be carried out. However, when the minor defective stage is identified, we adopt delaying maintenance and halving the subsequent inspection interval.

2. Modelling assumptions and notation

The following modeling assumptions and notation are presented for model building.

1) A single component system is considered, which only subject to a single failure mode.

2) The failure process of the system is divided into three stages: normal stage $X_{1}$ , minor defective stage $X_{2}$ and severe defective stage $X_{3}$ . These three stages are assumed to be independent.

3) The system is subjected to inspection interval $t$ and age based replacement interval $T$ . The age based replacement interval is a multiple of the inspection interval as $T = N t$ for simplicity.

4) The inspection is assumed to be imperfect, which may miss the minor defective stage with a probability of (1 $- r$ ) but always can identify the severe defective stage.

5) When the system is identified in the minor defective stage, we adopt shortening the subsequent inspection interval to be half of the current interval. Once the system is found to be in the severe defective stage, it is always repaired immediately. Failure can be observed immediately and replacement is always carried out at once. Replacement renews the system once the age of system reaches certain age $T$ , which is an age limit of system.

6) Repair or replacement is regarded as renewing the system, though it may be the only option for a single component system.

The subsequent modeling will use the following notation:

$X_{n}$ – Random variable representing the duration of the $n$ th stage, $n =$ 1, 2 and 3, $t$ – Inspection interval, $T$ – Age based replacement interval, $T = N t$ ( $N > 1$ ), $T_{f}$ – Random failure time, $T_{p m}$ – Random time of an inspection renewal due to the minor defective stage identification by an inspection, $T_{p s}$ – Random time of an inspection renewal due to the severe defective stage identification by an inspection, $T_{r}$ – Age based replacement time, $f_{X_{1}} (x)$ – Probability density function (pdf) of $X_{1}$ , $f_{X_{1}} (y)$ , $F_{X_{2}} (y)$ – pdf and cumulative distribution function (cdf) of $X_{2}$ , $f_{X_{3}} (z)$ , $F_{X_{3}} (z)$ – pdf and cdf of $X_{3}$ ,

3. The proposed optimization model based on a three-stage failure process

The optimization model is formulated in this section to jointly optimize the inspection and replacement intervals. The objective is to derive the maximum long-run availability. There exist three different kinds of renewal scenarios, namely failure renewal, inspection renewal caused by the identification of severe defective stage and age based replacement renewal.

3.1. The expected renewal cycle downtime

3.1.1. The failure renewal scenarios

Failure renewal means the system fails in an inspection interval before identifying the severe defective stage or reaching the certain age $T$ . However, according to whether the minor defective stage is identified by an inspection, there are two different failure renewals.

1) The system fails in $T_{f}$ , $T_{f} \in ((i - 1) t, i t)$ before any defective stages are identified, as shown in Fig. 1. The probability of such an event is given as:

1

\begin{matrix} P ((i - 1) t < T_{f} < i t) \end{matrix}

= P ((j - 1) t < X_{1} < j t, (i - 1) t - X_{1} < X_{2} < i t - X_{1}, 0 < X_{3} < i t - X_{1} - X_{2})

= \sum_{j = 1}^{i} \int_{(j - 1) t}^{j t} \int_{λ ((i - 1) t - x)}^{i t - x} (1 - r)^{i - j} f_{X_{1}} (x) f_{X_{2}} (y) F_{X_{3}} (i t - x - y) d y d x,

where $i =$ 1, 2,…, $N$ . Here we define $λ (x) = x$ if $x \geq 0$ , otherwise $λ (x) = 0$ .

Fig. 1The system fails in ((i-1)t, it) before any defective stages are identified

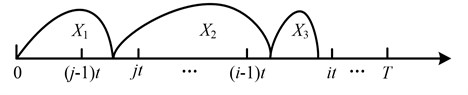
2) The system fails in $T_{f}$ , $T_{f} \in (i t + (k - 1) t / 2, i t + k t / 2)$ before identifying the severe defective stage by an inspection. However, the minor defective stage is identified at $i t$ and the subsequent inspection interval is halved, as depicted in Fig. 2. The probability of such a renewal is:

2

P (i t + (k - 1) t / 2 < T_{f} < i t + k t / 2)

= P (\begin{matrix} (j - 1) t < X_{1} < j t, i t + (k - 1) t / 2 - X_{1} < X_{2} < i t + k t / 2 - X_{1}, \\ 0 < X_{3} < i t + k t / 2 - X_{1} - X_{2}) \end{matrix})

= \sum_{j = 1}^{i} \int_{(j - 1) t}^{j t} f_{X_{1}} (x) \int_{i t + (k - 1) t / 2 - x}^{i t + k t / 2 - x} f_{X_{2}} (y) (1 - r)^{i - j} r F_{X_{3}} (i t + k t / 2 - x - y) d y d x .

Therefore, the expected downtime due to failure renewal can be derived as:

3

E D_{f} (t) = \sum_{i = 1}^{N} (D_{f} + (i - 1) D_{s}) P ((i - 1) t < T_{f} < i t)

+ \sum_{i = 1}^{N - 1} \sum_{k = 1}^{2 (N - i)} (D_{f} + (i + k - 1) D_{s}) P (i t + (k - 1) t / 2 < T_{f} < i t + k t / 2) .

Fig. 2The system fails in (it+(k-1)t/2, it+kt/2) after identifying minor defective stage at it

3.1.2. The inspection renewal scenarios

Inspection renewal occurs once the defective stage is identified. However, when the minor defective stage is identified, the subsequent inspection interval is halved.

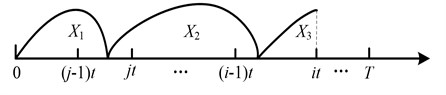
1) Fig. 3 shows the scenario that the system is renewed when the severe defective stage is found at $i t$ before any minor defective stage is identified. So the probability of such an inspection renewal is:

4

P (T_{p s} = i t) = P ((j - 1) t < X_{1} < j t, (i - 1) t - X_{1} < X_{2} < i t - X_{1}, X_{3} > i t - X_{1} - X_{2})

= \sum_{j = 1}^{i} \int_{(j - 1) t}^{j t} f_{X_{1}} (x) \int_{λ ((i - 1) t - x)}^{i t - x} f_{X_{2}} (y) (1 - r)^{i - j} (1 - F_{X_{3}} (i t - x - y)) d y d x .

Fig. 3The system renews at it before any minor defective stage is identified

2) Fig. 4 presents the scenario that the inspection renewal occurs at $i t + k t / 2$ when the minor and severe defective stages are identified at $i t$ and $i t + k t / 2$ respectively:

5

P (T_{p s} = i t + k t / 2)

= P (\begin{matrix} (j - 1) t < X_{1} < j t, i t + (k - 1) t / 2 - X_{1} < X_{2} < i t + k t / 2 - X_{1}, \\ X_{3} > i t + k t / 2 - X_{1} - X_{2} \end{matrix})

= \sum_{j = 1}^{i} \int_{(j - 1) t}^{j t} f_{X_{1}} (x) \int_{i t + (k - 1) t / 2 - x}^{i t + k t / 2 - x} f_{X_{2}} (y) (1 - r)^{i - j} r (1 - F_{X_{3}} (i t + k t / 2 - x - y)) d y d x .

Fig. 4The system renews at it+kt/2 after the minor defective stage is identified at it

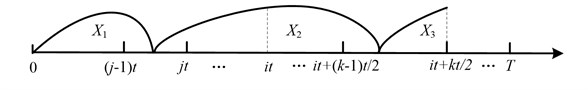
Then the expected downtime of an inspection renewal can be derived as:

6

E D_{s} (t) = \sum_{i = 1}^{N - 1} (D_{p s} + i D_{s}) P (T_{p s} = i t) + \sum_{i = 1}^{N - 1} \sum_{k = 1}^{2 (N - i) - 1} (D_{p s} + (i + k) D_{s}) P (T_{p s} = i t + k t / 2) .

3.1.3. The age based replacement renewal scenarios

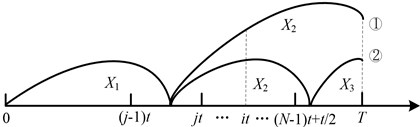
1) The age based replacement renewal is happened before any defective stage is identified. But there may exist three possible scenarios, see Fig. 5. The possibility of such a renewal is:

7

P (T_{r 1} = N t) = P (X_{1} > N t) + P ((j - 1) t < X_{1} < j t, X_{2} > N t - X_{1})

+ P ((j - 1) t < X_{1} < j t, (N - 1) t - X_{1} < X_{2} < N t - X_{1}, X_{3} > N t - X_{1} - X_{2})

= \int_{N t}^{\infty} f_{X_{1}} (x) d x + \sum_{j = 1}^{N} \int_{(j - 1) t}^{j t} (1 - r)^{N - j} f_{X_{1}} (x) (1 - F_{X_{2}} (N t - x)) d x

+ \sum_{j = 1}^{N} \int_{(j - 1) t}^{j t} (1 - r)^{N - j} f_{X_{1}} (x) \int_{(N - 1) t - x}^{N t - x} f_{X_{2}} (y) (1 - F_{X_{3}} (N t - x - y)) d y d x .

2) The system renews at age $T$ after the minor defective stage is found at $i t$ . There also exist two different scenarios, see Fig. 6:

8

P (T_{r 2} = N t) = P ((j - 1) t < X_{1} < j t, X_{2} > N t - X_{1})

+ P ((j - 1) t < X_{1} < j t, (N - 1) t + t / 2 - X_{1} < X_{2} < N t - X_{1}, X_{3} > N t - X_{1} - X_{2})

= \sum_{j = 1}^{i} \int_{(j - 1) t}^{j t} f_{X_{1}} (x) (1 - r)^{i - j} r (1 - F_{X_{2}} (N t - x)) d x

+ \sum_{j = 1}^{i} \int_{(j - 1) t}^{j t} f_{X_{1}} (x) (1 - r)^{i - j} r \int_{(N - 1) t + \frac{t}{2} - x}^{N t - x} f_{X_{2}} (y) (1 - F_{X_{3}} (N t - x - y)) d y d x .

The expected downtime of age based replacement renewal can be given as:

9

E D_{r} (t) = ((N - 1) D_{s} + D_{r}) P (T_{r 1} = N t) + \sum_{i = 1}^{N - 1} ((2 N - i - 1) D_{s} + D_{r}) P (T_{r 2} = N t) .

Fig. 5The system renews at age T before any defective stage is identified

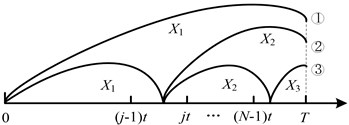
Fig. 6The system renews at age T after identifying the minor defective stage at it

3.2. The expected renewal cycle length

3.2.1. The failure renewal scenarios

The expected cycle length caused by failure renewal is expressed as:

10

E L_{f} (t) = \sum_{i = 1}^{N} \int_{0}^{t} ((i - 1) t + z) P ((i - 1) t + z < T_{f} < (i - 1) t + z + d z)

+ \sum_{i = 1}^{N - 1} \sum_{k = 1}^{2 (N - i)} \int_{0}^{\frac{t}{2}} (i t + \frac{(k - 1) t}{2} + z)

∙ P (i t + \frac{(k - 1) t}{2} + z < T_{f} < i t + \frac{(k - 1) t}{2} + z + d z) .

3.2.2. Inspection renewal scenarios

The expected renewal cycle downtime of inspection renewal is given as:

11

E L_{s} (t) = \sum_{i = 1}^{N - 1} i t P (T_{p s} = i t) + \sum_{i = 1}^{N - 1} \sum_{k = 1}^{2 (N - i) - 1} (i t + \frac{k t}{2}) P (T_{p s} = i t + \frac{k t}{2}) .

3.2.3. Age replacement renewal scenarios

The expected cycle length of age-based replacement renewal is given as:

12

E L_{r} (t) = N t P (T_{r 1} = N t) + \sum_{i = 1}^{N - 1} N t P (T_{r 2} = N t) .

3.3. The optimization model

Maximizing the availability is a main object of maintenance optimization. Based on the different expected renewal cycle downtime and length, the long run availability is given as:

13

A (T) = \frac{E L (T)}{E L (T) + E D (T)} .

4. Numerical example

In this section a numerical example is presented to demonstrate the efficiency of the proposed model and find the optimal inspection and replacement intervals. As the Weibull distribution is one of the most commonly used distributions in reliability [8], the three stages are assumed to follow Weibull distributions and the pdf of the $n$ th ( $n =$ 1, 2 and 3) stage is:

14

f_{X_{n}} (x) = a_{n} b_{n} (a_{n} x)^{b_{n} - 1} e^{- (a_{n} x)^{b_{n}}},

where $a_{n}$ , $b_{n}$ are scale parameter and shape parameter respectively. The distribution parameters are shown in Table 1.

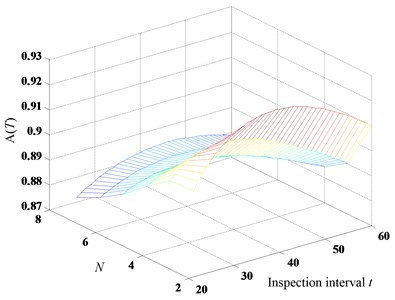
The downtime parameters are $D_{s} =$ 1, $D_{r} =$ 3, $D_{p m} =$ 5, $D_{p s} =$ 10, $D_{f} =$ 50, $r =$ 0.6. Depending on the given distribution and downtime parameters, we can determine the optimal decision variables and analyze the outputs of the proposed model. The result of the long run availability is presented in Fig. 7. The optimal intervals are $t^{*} =$ 38, $N^{*} =$ 2 with the maximum long run availability $A^{*} (T) =$ 0.9274.

Table 1Distribution parameters

$a_{1}$	0.016
$b_{1}$	1.14
$a_{2}$	0.018
$b_{2}$	1.78
$a_{3}$	0.0189
$b_{3}$	2.98

Fig. 7The long run availability

5. Conclusions

In this paper, a joint optimal policy of inspection and age based replacement for a single component based on a three-stage failure process is proposed aiming at jointly optimizing the inspection and replacement intervals. The system is replaced when it fails or reaches the age $T$ . Once the severe defective stage is identified, maintenance action is carried out. When the minor defective stage is identified, the subsequent inspection interval is halved. The optimal inspection and age replacement intervals are found in the numerical example.

References

Nicola R. P., Dekker R. Optimal maintenance of multi-component systems: a review. Complex system maintenance handbook. Amsterdam, Springer, 2008.

Search CrossRef
Wang W., Dragan B., Michael P. A multi-component and multi-failure mode inspection model based on the delay time concept. Reliability Engineering and System Safety, Vol. 95, 2010, p. 912-920.

Search CrossRef
Yang R. F., Kang J. S., Zhang X. H., Teng H. Z., Li H. P. Application of SPM to detect the wind turbine bearing fault. Journal of Electrical Engineering, Vol. 12, Issue 3, 2014, p. 1875-1880.

Search CrossRef
Wang W. An inspection model based on a three-stage failure process. Reliability Engineering and System Safety, Vol. 96, 2011, p. 838-848.

Search CrossRef
Wang W., Zhao F., Peng R. A preventive maintenance model with a two-level inspection policy based on a three-stage failure process. Reliability Engineering and System Safety, Vol. 121, 2014, p. 207-220.

Search CrossRef
Barlow R. E., Proschan F. Mathematical Theory of Reliability. Wiley, New York, 1965.

Search CrossRef
Jiao G., Zuo M. J. Comparison of maintenance policies in hazard rate order. 8th International Conference on Reliability, Maintainability and Safety, Chengdu, 2009, p. 224-227.

Search CrossRef
Murthy D. N. P., Xie M., Jiang R. Weibull models. Willey, New Jersey, 2004.

Search CrossRef

About this article

Received

Accepted

14 September 2014

Published

03 November 2014

Keywords

condition-based maintenance

inspection

three-stage failure process

age based replacement

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.