Abstract
A new feature extraction method based on WPD and Entropy is proposed in this paper. Firstly, WPD is utilized to decompose the signal into different frequency bands to obtain different frequency sub-signal. Secondly, root-mean-squire (RMS) value, kurtosis (K) and peak factor (PF) parameters are extracted from each sub-signal to obtain the fault feature vector. Thirdly the Entropy of each feature vector is calculated to realize the bearing fault diagnosis. Finally, experimental results indicate that the bearing fault diagnosis method proposed in this paper is effective.
1. Introduction
Rolling bearing is widely used in industry. It is a key component of aircraft engine, steam turbine, and so on. The fault of bearing may cause the crash of whole system. So the research of the bearing fault diagnosis is very significant. The bearing fault diagnosis method contains oil samples analysis, temperature analysis and vibration signal analysis. From the literature research [1], the vibration signal analysis method has advantage in bearing fault diagnosis. The fault feature vectors are extracted from the vibration signal which is processed by signal process method, for further fault diagnosis. The universal vibration signal process method is Fourier transform [2-3]. Beacause the bearing vibration signal is complex and non-stationary, the frequency spectrum analysis can’t meet the requirements. So in recent years, a series of time-frequency analysis are applied in bearing fault diagnosis. Winger-Ville distribution has the inevitable cross term defects [4]. The Wavelet analysis can decompose the low frequency parts of signal into different frequency bands. However, the information of high frequency signal can’t be reflected. The Wavelet package decomposition [5], as a new time-frequency analysis method, not only can decompose the low frequency parts of the signal but also the high frequency, which can reflect the whole frequency bands of the signal.
Another challenge of bearing fault diagnosis is fault feature extraction. Time-domain features are widely applied in this field. These time-domain parameters which can reflect the characters of signal from different aspects are simple, effective, so three time-domain parameters of each sub-signal are extracted in this paper. The root mean value (RMS) can reflect the signal energy. The kurtosis reflects the signal distribution characters. The crest factor is sensitive to plus signal. As the bearing vibration signal is complex and non-stationary, these time-domain parameters can’t reflect the characteristic comprehensively. From the literature research we found that Shannon Entropy can be qualified in information measurement [6-7]. In this paper we introduce Entropy to quantify the vibration signal, the more complex the signal, the larger the Entropy. So in this paper, we proposed a feature extraction method based on wavelet package decomposition (WPD) and Entropy. As bearing breaks down, the time-domain parameters of the fault signal, changes. So the Entropy of different time-domain parameters can reflect the bearing fault effectively.
This paper is organized as follows. In the section 2 we introduced the fault feature extraction method proposed in this paper. In this section the theory of WPD and Entropy are also introduced. In section 3 we introduced a bearing fault diagnosis case study. The fault feature extracted method is verified by the experiment.
2. Bearing diagnosis method based on WPD-Entropy
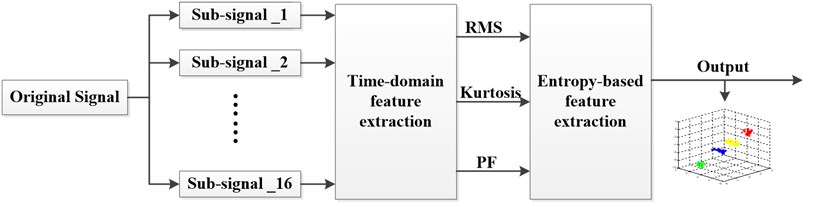
This paper proposed a new bearing fault extraction method based on WPD-Entropy. As the bearing vibration signal is nonlinear and non-stationary, we use wavelet package decomposition (WPD) to process this signal [8]. By conducting a 4 level WPD, the original signal is divided into 16 different frequency bands. Thus we can get 16 sub-signals. After that three time-domain parameters were extracted from these sub-signals. So we can get 48 fault features belonging to three different time-domain parameters. For each time-domain parameters we can get a fault feature vector which contains 16 elements. Next, we calculate the Entropy of each time-domain parameters. Thus, the three Entropy values construct the fault feature vector. The flow chart of the method proposed in this paper is shown in Fig. 1.
Fig. 1The flow chart of the bearing diagnosis method based on WPD-Entropy
2.1. Application of wavelet package on bearing vibration signal
Wavelet package Decomposition (WPD) is a new time-frequency analysis method which has the high frequency resolution in the low frequency and high time resolution in the high frequency. By projecting signal on a set of orthogonal wavelet basis function, WPD decomposes signal into low frequency part and high frequency part. WPD not only decomposes the low-frequency of the signal, but also can decompose the high frequency. So wavelet package decompose is a more precise time-frequency analysis method. The Wavelet package decomposition diagram is shown in Fig. 2.
Fig. 2Wavelet package decomposition diagram
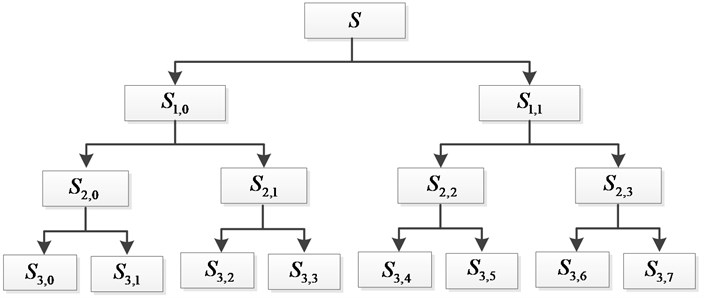
By decomposing the high frequency signal obtained from the wavelet decomposition, the wavelet package decomposes signal into ( is the decomposition level) decomposition level numbers of wavelet package space. The wavelet package decomposition algorithm is as follows:
The Wavelet package reconstruction algorithm is as follows:
where , are wavelet package decomposition coefficients; , are low pass and high pass filter of wavelet package decomposition respectively; , are low pass and high pass filter of wavelet package reconstruction respectively.
In this paper we utilize wavelet package decomposition to process the bearing vibration signal. We conduct 4-level wavelet package decomposition. Thus the original signal is decomposed into 16 frequency bands.
2.2. Entropy-based feature extraction
In this section, we introduce the Entropy-based feature extraction method. The bearing vibration signal is decomposed into 16 frequency bands. For each sub-signal we extracted three time-domain features. Thus we can get 16 values for each time-domain features. So for each time-domain feature, we can get a feature vector which contains 16 features of different sub-signal. After that, we calculate the Entropy of the three time-domain features by using the three feature vectors obtained from sub-signal. At last the bearing feature vector was extracted by using Entropy-based feature extraction method.
2.2.1. Time-domain features
The three time-domain features are root-mean-squire (RMS) value, kurtosis () and peak factor (PF). The formula of the features is as follows:
2.2.2. The theory of entropy
In 1948, C. E. Shannon introduced the concept of Entropy into information theory. The definition of Shannon Entropy is as follows:
where is random variables; is the probabilistic set of is a Boltzmann constant. In this paper we calculate the Entropy of three time-domain parameters. Take example for the RMS, we can get a RMS feature vector . Where is the probability of . Then the Entropy of RMS can be described as . Then the Entropy of three parameters can be calculated by the method above.
3. Case study of bearing fault diagnosis
In this section, we introduce a case study of bearing fault diagnosis based on WPD-Entropy proposed in this paper. The deep groove ball bearing is used in experiment. The geometric parameters of the bearing are shown in Table 1. We collected bearing vibration signal with 12000 samples per second in normal, outer ring fault, inner ring fault and rolling element fault state.
Table 1The geometric parameters of the bearing
Inside diameter | Outside diameter | Thickness | Ball diameter | Pitch diameter |
25 (mm) | 52 (mm) | 15 (mm) | 7.9 (mm) | 39 (mm) |
3.1. Application of WPD on bearing vibration signal process
In this paper, there are three fault bearing vibration signal and a normal signal. We conduct a 4 level WPD to decompose these signal into 16 different frequency bands.
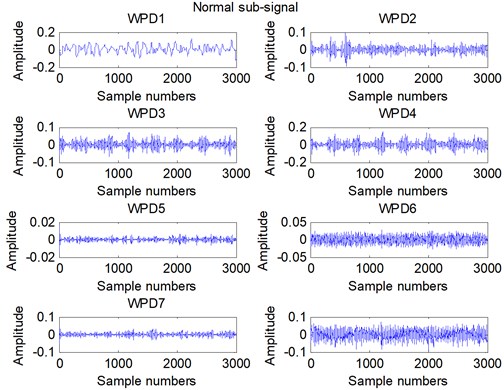
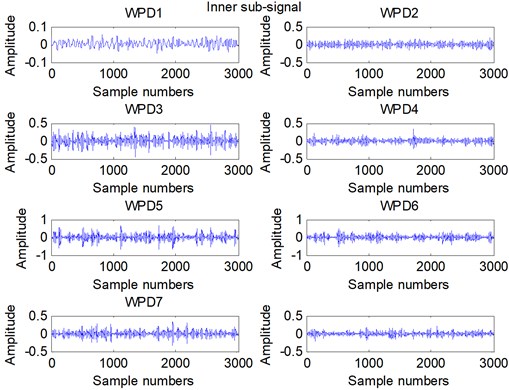
In this experiment, we collect 4 different fault signals. We collect normal, rolling element fault, Inner ring fault and Outer ring fault bearing vibration signals with sample frequency 12000 Hz. We decompose the bearing vibration signal into 16 sub-signals. The first ten sub-signals are shown in Fig. 3.
From the Fig. 3, we can see that the sub-signals of different fault are significantly different. We can distinguish the different fault from the shape of sub-signal. So the WPD can decompose the bearing signal and display the fault feature preliminarily.
3.2. Entropy based extraction
50 samples of each fault are selected and processed by the proposed method. After the signal is decomposed into different frequency bands, we extract three time-domain parameters of the sub-signals and calculate the Entropy of the three parameters to construct fault feature vector. The extracted fault features are shown in Fig. 4.
As is shown from the Fig. 4, the bearing faults are classified clearly. The different fault data samples are located in different locations in the feature space. So the fault feature extraction based on WPD-Entropy proposed in this paper can distinguish the bearing fault effectively.
Fig. 3Sub-signal obtained from WPD
a)
b)
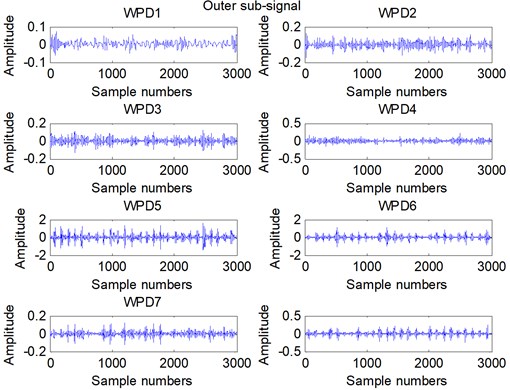
c)
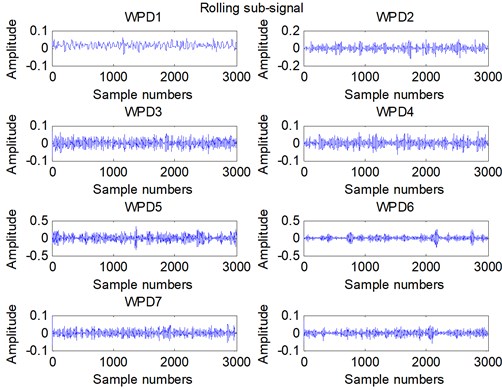
d)
Fig. 4Classification result of bearing fault
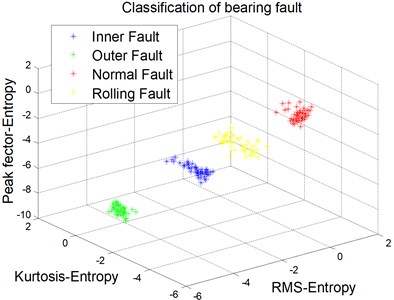
4. Conclusions
In this paper, we proposed the fault feature extraction method based on WPD-Entropy. The vibration signal is decomposed into 16 frequency bands. Then we calculate time-domain parameters of each sub-signal. After that, the Entropy of each parameter is calculated to construct the fault feature vector. The experiment results show that the WPD can decompose the complex signal and reflect the characters of signal in different frequency bands effectively. The fault feature extraction based on Entropy can distinguish different bearing fault signal effectively. Different fault vector are located in different locations. So, the WPD-Entropy based feature extraction method is effectively in bearing fault diagnosis.
References
-
Wu Lifeng, Zheng Xueyan, Guan Yong, Wang Guohui, Li Xiaojuan A survey of fault diagnosis technology for electronic circuit based on knowledge technology, Capital Normal University Beijing, Beijing, China.
-
Figueiredo A. C. A., Nave M. F. F., Contributors E. J. E. T. Time-frequency analysis of non-stationary signals in fusion plasmas using the Choi–Williams distribution. Nuclear Fusion, Vol. 44, Issue 10, 2004.
-
Feng Z., Liang M., Chu F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mechanical Systems and Signal Processing, Vol. 38, 2013, p. 165-205.
-
Xiao Siwen, Liao Chuanjun, Li Xuejun Applications of Wigner high-order spectra in feature extraction of acoustic emission signals. Engineering Sciences, Vol. 3, 2009, p. 59-65.
-
Sun Fang, Wei Zijie Rolling bearing fault diagnosis based on wavelet packet and RBF neural network. Control Conference, 2007, p. 451-455.
-
Li Jian-Lan, Huang Shu-Hong Fault diagnosis of a rotary machine based on information entropy and rough set. International Journal of Plant Engineering and Management, Vol. 4, 2007, p. 199-206.
-
Geng Jun-bao, Huang Shu-hong, Jin Jia-shan, Chen Fei, Liu Wei A method of rotating machinery fault diagnosis based on the close degree of information entropy. International Journal of Plant Engineering and Management, Vol. 3, 2006, p. 137-144.
-
Tong Yubing, Yang Dongkai, Zhang Qishan Wavelet Kernel support vector machines for sparse approximation. Journal of Electronics, Vol. 23, Issue 4, 2006, p. 539-542.
About this article
This research was supported by the National Natural Science Foundation of China (Grant No. 61074083, 50705005, and 51105019), and by the Technology Foundation Program of National Defense (Grant No. Z132013B002).
