Abstract
In order to realize fault diagnosis of the rolling bearing, a fast and effective method based on empirical wavelet transform (EWT) and extreme learning machine (ELM) is proposed in this paper. Bearing vibration signals, which contain a large amount of fault information, can be decomposed into multiple single components adaptively, from which the characteristic vectors suitable for diagnosis can be extracted. ELM has the advantages of fast learning speed and good generalization performance, which makes it possible to diagnose fault patterns of bearings easily. The case study based on experiment data proves the feasibility of this method.
1. Introduction
For many rotating machines, rolling bearings play an important role. Bearing fatigue can lead to failure of the inside and outside raceways and rolling elements, which can be characterized by vibration signals [1]. This paper presents an efficient fault diagnosis method based on empirical wavelet transform (EWT) and extreme learning machine (ELM).
Due to the complex working environment of the bearings, the vibration signals of the bearings are affected by the impact caused by the faults and the multi-carrier modulation occurs. The advanced diagnosis methods for rolling bearing faults are based on time-frequency domain decomposition of signals, such as short time Fourier transform (STFT), wavelet transform, empirical mode decomposition (EMD) and local mean decomposition (LMD). By combining the adaptability of dividing the signal spectrum in EMD into wavelet transform, a new method called empirical wavelet transform (EWT) changed the traditional spectrum division of binary wavelet. EWT is proved to be able to separate different modes, which is one of the most powerful time-frequency methods to deal with non-stationary data [2]. Thus, EWT is used to extract the sensitive information existing in vibration signals in this paper.
Extreme learning machine (ELM), an intelligent algorithm which performs well in regression and multi-classes classification problems, has attracted more and more researchers’ attention. Meanwhile, ELM has been proven to be more efficient and smarter than support vector machine (SVM) and BP neural network [3]. Thus, in this study, ELM is introduced to classify the fault states of the rolling bearing based on the features extracted through EWT.
This paper is organized as follows: Section 2 introduces EWT and ELM, Section 3 describes the case study performed to validate the method, and Section 4 presents the conclusions and related future works.
2. Methodology
2.1. Empirical wavelet transform
Empirical wavelet transform is a recently proposed method for adaptive detection of different members, which is similar with empirical mode decomposition method [4]. In frequency domain, an empirical wavelet refers to the process of building a set of wavelets, which is equivalent to build a set of band-pass filters. Inspired by EMD method, EWT method detects the filters’ supports based on the information existing in the original signal, which makes it possible of EWT to decompose the signals adaptably. These modes are amplitude modulated-frequency modulated (AM-FM) components that have compact support Fourier spectrum [5]. Therefore, detecting different modes is similar to splitting the Fourier spectrum and applying filtering according to the support. The purpose of EWT is to decompose the into mono-components , respectively:
where is defined as an AM-FM function which is denoted as:
Assuming that the Fourier support is segmented into contiguous segments. is denoted to be the limits between each segment (where 0 and ). Each segment is denoted as , and . Centered around each , a transition phase , is defined of width and . is properly chose to get a tight frame and is given in Eq. (3):
The empirical wavelets are defined as band-pass filters on each . For 0, the empirical scaling function and the empirical wavelets are defined by Eqs. (4), (5), respectively:
Commonly, is defined as [6].
The EWT can be defined as same as for the classic wavelet transform. The detail coefficients are given by inner products with the empirical wavelets:
and the approximation coefficients by inner product with the scaling function:
The reconstruction is obtained by:
where represents faltung. Moreover, the empirical mode is given as follows:
2.2. Extreme learning machine
ELM is a newly developed learning algorithm proposed by Huang et al. [7], which has faster learning speed and better generalization performance. ELM is a special kind of single hidden layer feed forward neural network, which only has one hidden node layer. It was extended to a general single hidden-layer feedforward neural network. Fig. 1 shows the basic structure of ELM.
Fig. 1Basic structure of ELM
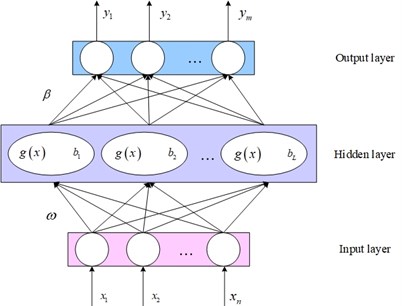
In Fig. 1, represents the input samples. represents the vector of link weights between all nodes in the input layer and hidden layer. represents the activation function of the hidden layer. represents the bias of neurons in the hidden layer. represents the vector of link weights between the th node in the hidden layer and all nodes in the output layer. represents the output of the network. , , represent the number of nodes in the input layer, hidden layer and the output layer, respectively. The mathematical model of ELM is denoted as:
The activation function utilized in this study is sigmoid function, which is denoted as:
2.3. Fault diagnosis procedure based on EWT and ELM
The proposed method has two steps. (1) Vibration signal decomposition utilizing EWT to obtain the components which contain the fault information, as well as eliminating noise existing in the original signal. (2) Fault diagnosis based on the ELM classification model, which takes the features consist of energy from the selected components as input. The process of the method is summarized in Fig. 2.
Fig. 2Process of the proposed method
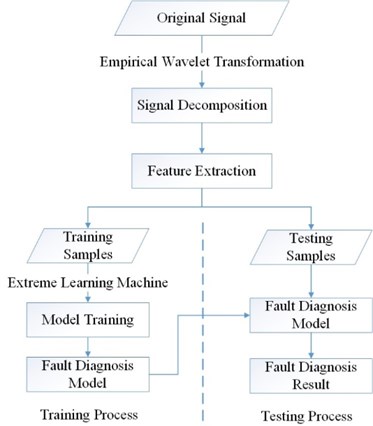
3. Validation
3.1. Introduction to validating data
In order to validate the practicability and high efficiency of the method, the experiment data of the Case Western Reserve University Bearing Data Center were used in the case study of this paper [8]. As shown in Fig. 3, the test stand consists of a motor (left), a torque transducer (center), a dynamometer (right), and control electronics (not shown). The test bearings support the motor shaft.
Motor bearings were seeded with faults using electro-discharge machining (EDM). Faults with a diameter of 0.007 inches were introduced separately at the inner raceway, rolling element and outer raceway. Vibration data was collected using accelerometers, which were attached to the housing with magnetic bases.
Fig. 3The test stand

3.2. Signal decomposition based on EWT
To acquire the fault feature vectors, the original vibration signals are decomposed into several components using EWT. Fig. 4 shows the decomposed components of the rolling bearing’s normal state and fault state.
EWT adaptively decomposes fault signals and normal signals into different components. As the figures show, the patterns of the components are obviously different in normal and fault states. Thus, the decomposing results could be used to classify the states of the rolling bearing. For the purpose of improving the performance of the fault diagnosis model, the energy and kurtosis index of the three most important components are extracted to form the feature vector. Table 1 shows some of the obtained feature vectors of the samples that belong to each fault state.
Fig. 4EWT result of: a) normal state, b) inner raceway fault state
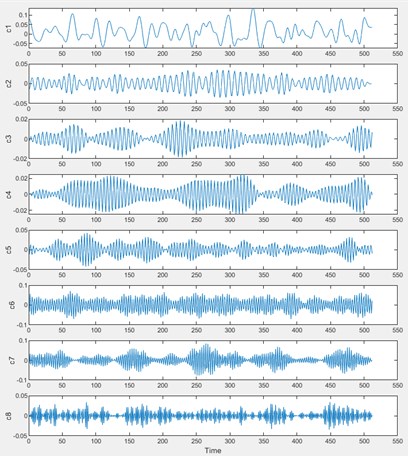
a)
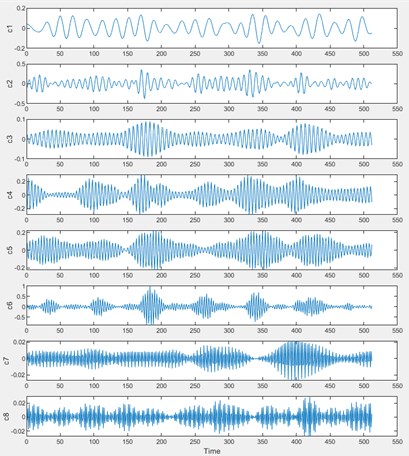
b)
Table 1Feature vectors obtained by EWT
Normal | Inner raceway fault | Rolling element fault | Outer raceway fault | |||||
1 | 1.905 | 1.729 | 3.023 | 3.951 | 2.543 | 2.036 | 4.463 | 5.470 |
2 | 0.331 | –0.024 | –0.023 | –0.070 | 0.000 | 0.000 | 0.022 | 0.000 |
3 | 2.679 | 2.822 | 5.573 | 5.292 | 2.605 | 2.466 | 6.831 | 8.360 |
4 | 0.362 | 0.413 | 0.178 | 0.229 | 0.068 | 0.036 | 0.027 | 0.020 |
5 | 0.476 | 0.485 | 0.197 | 0.417 | 0.185 | 0.044 | 0.384 | 0.412 |
6 | 0.786 | 0.649 | 0.948 | 0.845 | 0.978 | 0.998 | 0.923 | 0.911 |
3.3. Training of ELM model for fault diagnosis
Four states of the rolling bearing were considered, including normal state and three fault states. The vibration data in the four states were used for training the fault diagnose model based on extreme learning machine, 96 sets of data per state. In other words, the training dataset contained 384 sets of data.
3.4. Validation of the proposed method
For the purpose of validating the proposed method, 32 sets data under each state were selected to form the testing sample. Thus, the testing dataset consisted of 128 sets of data in total. The testing dataset was processed by the fault diagnosis model trained above. The corresponding labels of normal state and fault states were 1/2/3/4 respectively. The actual states of the rolling bearing are shown in Fig. 5(a), where the ordinate value indicates the state of the rolling bearing. The testing results are shown in Fig. 5(b).
The result shows that the fault diagnosis based on EWT-ELM method reaches the accuracy of 100 %, which indicates that the proposed is capable of distinguishing the states of the rolling bearing under different fault modes.
Fig. 5The actual state of: a) rolling bearing, b) testing result
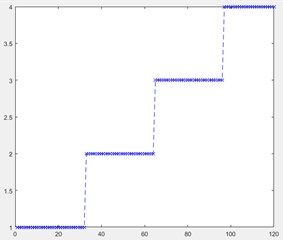
a)
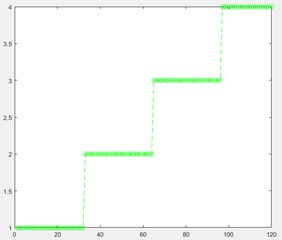
b)
4. Conclusions
Fault diagnosis for the rolling bearing based on empirical wavelet transform and extreme learning machine was performed in this study. EWT can decompose the original vibration signals adaptively and obtain appropriate features from non-stationary vibration signals. ELM model is an effective tool for fault classification. It can be seen from the validation results that this method is suitable for the diagnosis of the rolling bearing. Furthermore, additional fault modes should be taken into consideration to achieve a comprehensive performance on rolling bearing fault classification.
References
-
Al Ghamd A.-M., Mba D. A comparative experimental study on the use of acoustic emission and vibration analysis for bearing defect identification and estimation of defect size. Mechanical Systems and Signal Processing, Vol. 20, Issue 7, 2006, p. 1537-1571.
-
Huang N. E., Shen Z., et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings Mathematical Physical and Engineering Sciences, Vol. 454, 1971, p. 903-995.
-
Tian Y., Ma J., Lu C., Wang Z. Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine. Mechanism and Machine Theory, Vol. 90, 2015, p. 175-186.
-
Gills J. Empirical wavelet transform. IEEE Transactions on Signal Processing, Vol. 61, Issue 16, 2013, p. 3999-4010.
-
Daubechies I., Lu J., Wu H. T. Synchro squeezed wavelet transforms: An empirical mode decomposition-like tool. Applied and Computational Harmonic Analysis, Vol. 30, Issue 2, 2011, p. 243-261.
-
Daubechies I. Ten lectures on wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics, 1992.
-
Huang G. B., Zhu Q. Y., Siew C. K. Extreme learning machine: theory and applications. Neurocomputing, Vol. 70, Issue 1, 2006, p. 489-501.
-
Bearing Data Center, Case Western Reserve University, http://csegroups.case.edu/bearingdatacenter/home.
Cited by
About this article
This research was supported by the National Natural Science Foundation of China (Grant Nos. 51605014, 51105019 and 51575021), the Aviation Science Fund (Grant No. 20163351018), the Technology Foundation Program of National Defense (Grant No. Z132013B002)], and the Fundamental Research Funds for the Central Universities (Grant No. YWF-18-BJ-Y-159).
