Motor rolling bearing fault diagnosis based on MVMD energy entropy and GWO-SVM

2.1. Multivariate variational mode decomposition

The MVMD method extends VMD algorithm from one-dimensional to multidimensional, which provides great convenience for processing multi-variable or multi-channel data, and ensures component frequency consistency during multi-channel decomposition [13]. MVMD method for component method is based on the input data of all the channel between the common frequency component, in the process of signal decomposition is introduced into the variational model, construct a change model of the optimal solution of the problem, in this process, the channel mode of component and iterative update its center frequency and bandwidth, which can be adaptive to $k$ component of narrow band mode [18].

Given input multivariate signal $\mathbf{X}\left(t\right)$, MVMD can extract $K$ pre-defined multivariate modulated oscillation signals ${\mathbf{u}}_k\left(t\right)$ containing $C$ channel data [19]-[21]:

where ${\mathbf{u}}_k\left(t\right)=\left[u_1\left(t\right),u_1\left(t\right),\cdots ,u_c\left(t\right)\right]$, $\mathbf{X}\left(t\right)=\left[x_1\left(t\right),x_2\left(t\right),\cdots ,x_c\left(t\right)\right].$

To complete the iteration of MVMD algorithm, the following two conditions should be met:

1) The sum of bandwidth of the extracted modes is minimum;

2) The sum of the extracted modes can recover the original signal ${\mathbf{u}}_k\left(t\right)$.

The variational problem solved by MVMD can be expressed by the following equation:

where in the above formula, ${\partial }_t$ is the partial derivative of time. $u_{﹢}^{k,c}\left(t\right)$ is the vector expression of $u_{k,c}（t）$:

where in the above formula, $L\left(\left\{u_{k,c}\right\},\left\{{\omega }_k\right\},{\lambda }_C\left(t\right)\right)$ stands for augmented Lagrange function, $\alpha$ is the punishment factor. $\left\{u_{k,c}（t）\right\}$ is the set of multivariable modulated oscillating signals in channel $C$, ${\{\omega }_k\}$ is the central frequency set of $\left\{u_{k,c}（t）\right\}$ , the ${\lambda }_c\left(t\right)$ is the Lagrange multiplier. $〈·,·〉$ for inner product. For minimization problems related to pattern update, its equivalent optimization form is:

where in the above formula, $n$ is the number of iterations. This function is similar to the mode update of the original VMD in form, and the following mode update relation can be given by using Eq. (4):

where in the above formula, ${\widehat{x}}_c\left(\omega \right)$ and ${\widehat{\lambda }}_c\left(\omega \right)$ are the Fourier transform of the corresponding time domain signal. Simplification problem:

Let the first derivative of the above quadratic function Eq. (6) be 0, minimize the sum of $k$ quadratic functions, and then carry out algebraic operation, we can get:

where ${\omega }_k^{n+1}$ is the updated center frequency.

2.2. Energy entropy

The frequency distribution of motor bearing vibration signals in normal working state is different from that in different faults, that is, the energy distribution of vibration signals is different. Using the percentage of signal energy of each frequency band in the total energy and energy entropy (EE), the feature vector can be used to reflect the running state of the bearing [22].

After MVMD decomposition of bearing vibration signal, ${Mode}_k(k=\mathrm{1,2},\cdots ,K)$ can be obtained:

where $E_i(i=\mathrm{1,2},\cdots ,K)$ is energy, ${\stackrel{-}{E}}_i(i=\mathrm{1,2},\cdots ,K)$ is the energy percentage and $H_{En}$ is the energy entropy of each mode component.

The mode component obtained by decomposition contains different frequency components and has different energy characteristics, which constitutes the energy distribution of motor bearing vibration signal in the frequency domain. The motor bearing fault feature vector is constructed by it:

2.3. Grey wolf optimization

The GWO algorithm is a new meta-heuristic optimization algorithm proposed by Mirjalili S. et al. [23]. The algorithm has good convergence speed and optimization accuracy, and has been widely used in many fields. The grey wolf optimization algorithm simulates the hierarchy leadership mechanism of the social organization of the grey wolf population, including the group hunting behavior from hunting prey, circling prey to hunting, and obtains the position of the optimal solution through continuous iterative optimization. The GWO algorithm can imitate the wolf pack behavior process, which is mainly divided into three steps: encircle, hunt and attack. Inside the pack, there are four types of search individuals in descending order: $\alpha$, $\beta$, $\delta$ and $\omega$.

In this process, the species will circle its prey to find the best route to hunt. The location of target and optimal population in the encircling stage can be determined by Eq. (12-13) [23], [24]:

where the $t$ is the current number of iterations, $\mathbf{A}$, $\mathbf{C}$ and $\mathbf{D}$ are the coefficient vectors, ${\mathbf{X}}_p\left(t\right)$ is the target optimal solution vector (the location of prey), $\mathbf{X}\left(t\right)$ is the current position vector of a search individual, and $\mathbf{X}(t+1)$ is the next moving direction vector. $\mathbf{A}$ and $\mathbf{C}$ can be represented as follows [24]:

where the $M$ is the maximum number of iterations, a linearly decreases from 2 to 0 as the number of iterations $t$ increases, and ${\mathbf{r}}_1$ and ${\mathbf{r}}_2$ are the random vectors between [0, 1]. According to Eq. (15-16), the location of the points around the optimal solution can be searched by adjusting the size of the coefficient vectors of $\mathbf{A}$ and $\mathbf{C}$ to ensure the local optimization ability of the algorithm. ${\mathbf{r}}_1$ and ${\mathbf{r}}_2$ are random numbers between [0, 1], so the optimization population can find all the paths of the attacking target, while ensuring the global search ability of the algorithm.

When hunting and attacking prey, $\omega$ moves in the next step according to the signals sent by $\alpha$, $\beta$ and $\delta$ to judge whether it is close to the target or far away. The specific process can be expressed by Eq. (17-19) [23]-[25]:

where ${\mathbf{D}}_{\alpha }$, ${\mathbf{D}}_{\beta }$ and ${\mathbf{D}}_{\delta }$ are the direction vectors between $\alpha$, $\beta$, $\delta$ and $\omega$, respectively. The ${\mathbf{X}}_1$, ${\mathbf{X}}_2$ and ${\mathbf{X}}_3$ are respectively $\alpha$, $\beta$ and $\delta$ to determine the direction vector of $\omega$ next move.

2.4. GWO-SVM

The SVM has good performance for small sample classification learning. However, during network learning, the training network parameters need to be set, among which the penalty factor parameters ($c$) and kernel function parameters ($g$) in the network have a great influence on the classification results. The GWO algorithm realized the modeling of the whole iterative optimization process according to the hierarchical division of labor system and hunting behavior of wolves. In this paper, the GWO algorithm is applied to the measured energy entropy feature extraction value to optimize the parameters of network classification. Through different training samples of the input network, a group of appropriate $c$ and $g$ values are selected to better improve the network training performance and further improve the classification results.

3.1. Flow chart of experiment

The whole process of the experiment is shown in Fig. 1. Firstly, data sets of different working conditions of the motor rolling bearing are collected. Then MVMD decomposition is performed on the data set to obtain sub-band signals containing different characteristic information. The energy entropy of the decomposed sub-band signals was measured, and the energy features were classified by SVM classifier. The optimization algorithm GWO was used to optimize the parameters of the classification network to further improve the recognition accuracy. Finally, the recognition results were analyzed.

Fig. 1Motor rolling bearing fault diagnosis flow chart

3.2. Experimental data and simulation environment

The data set used in the experiment was obtained from the bearing failure simulation test bench in the laboratory of Case Western Reserve University, Fan end bearing model is SKF6205 deep groove ball bearing. Local damage of rolling bearing is single point damage by electro-discharge machining (EDM). Data of fault driving end of rolling element are selected. The rolling bearing equipment of the experimental motor is shown in Fig. 2, and its structural parameters are shown in Table 1. In the motor 0 HP/1797 r/min, 1 HP/1772 r/min, 2 HP/1750 r/min and 3 HP/1730 r/min four working conditions (data 1~data 4), take different training sample sets and test sample sets. The normal working state, inner ring fault, rolling element fault and outer ring fault are classified and identified. The specific sample set used in the experiment is shown in Table 2. The four groups of data correspond to four different working states of the motor rolling bearing.

Fig. 2Experimental data acquisition equipment for motor rolling bearing

Fig. 3 shows the time domain diagram of sensor vibration acceleration of data 1 under normal working state and three fault states. As can be seen from the figure, the amplitude of the collected signal under normal working condition is the smallest, and the amplitude of the inner ring is the largest. The time-domain signal diagram of the rolling element fault is close to that of the outer ring fault. It is easy to misdiagnose the fault category directly from the time domain signal diagram.

Fig. 3Working state of Data 1 motor

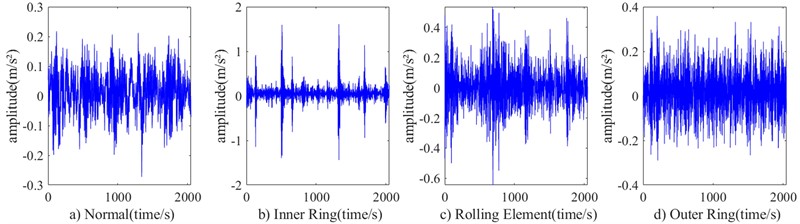
Fig. 4 shows the information features of different scales obtained by MVMD when MVMD decomposes the time-domain vibration signals in four working states of the motor in data 1. Fig. 4(a1)-(a4) is the decomposition time domain diagram under normal working condition, Fig. 4(b1)-(b4) is the decomposition time domain diagram under inner ring fault working condition, Fig. 4(c1)-(c4) is the decomposition time domain diagram under rolling element fault working condition, and Fig. 4(d1)-(d4) is the decomposition time domain diagram under outer ring fault working condition. The variation trend of different working states can be seen from the subgraphs of each time domain.

Fig. 4Data1 when K= 4, the four types of signals are decomposed by MVMD: a1)-a4) normal; b1)-b4) inner ring; c1)-c4) rolling element; d1)-d4) outer ring

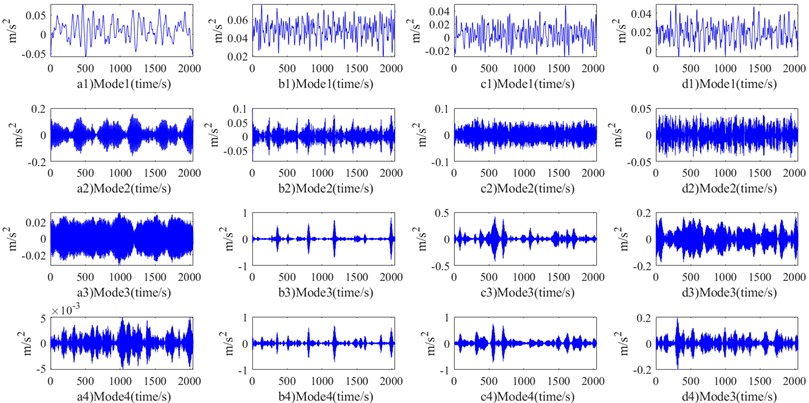
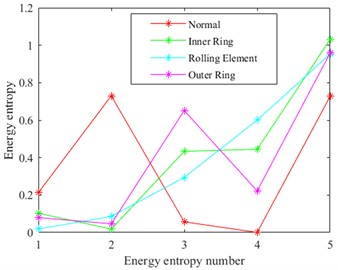
Fig. 5 shows the energy entropy measurement characteristic values of different scale information of MVMD decomposition. It can be seen from the characteristic values that the state modes of different motors rolling bearing work differently in the measurement values of different characteristic scale information. According to this feature, a SVM with good classification and separateness for small samples is used to classify the entropy eigenvalues of different states. Meanwhile, the optimization algorithm GWO is used to optimize the parameters of the identified and classified network, so as to further improve the classification ability of the network.

The simulation environment of this paper is the Inter (R) Core (TM) i5-8300H CPU @2.30GHz, memory 8.00GB 64-bit Windows 10 operating system for preliminary exploration. The simulation tool uses MATLAB R2020b version.

Fig. 5Energy entropy diagram of four working state signals of data1 decomposed by MVMD

3.3. The experimental results

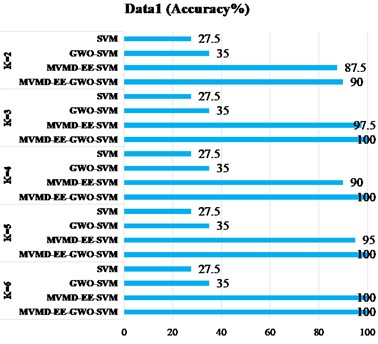
The Fig. 6 shows the result graph of recognition accuracy of four types of data sets under different feature extraction methods. The “Accuracy” in Fig. 6 represents the ratio of all predicted sample labels to actual labels in four working states of the motor rolling bearing. The closer the ratio is to 100 %, it indicates that the proposed prediction model is closer to our expectation. The subgraph (a) in Fig. 6 compares the four schemes respectively. The use “SVM” to classify directly; The “GWO-SVM” means classification of SVM network optimized by GWO; The “MVMD-EE-SVM” is used to indicate that vibration signals are decomposed first, and then classified after energy entropy measurement. The “MVMD-EE-GWO-SVM” is used to mean that vibration signals are first decomposed, then measured by energy entropy, and then GWO is used to optimize SVM classification. In the subgraphs (b) to (d) of Fig. 6, the above four schemes were used for experimental analysis of the other three sets of data. In the experiment, we analyzed the prior parameter $K$ value, which has a great influence on MVMD. The following conclusions can be drawn from the identification results: 1) Classify data in different states directly from time-domain signals, and the recognition and classification effect are poor. 2) By measuring the energy entropy characteristics of time-domain signals, the identification accuracy has been significantly improved, indicating that energy entropy can well represent the time-domain signal characteristics of mechanical vibration; 3) The four types of data are analyzed for different parameter $K$ values. According to the results, there are a small number of mismarks in the classification results of the eigenvalues measured by energy entropy, and the classification performance of the classifier is also an important index affecting the classification results. By optimizing the SVM network by GWO, the classification accuracy can reach 100 %. It provides higher feasibility for practical application.

In Table 3 to Table 6, we conducted statistical analysis on the feature extraction time and total time of four types of states in different data sets under different prior $K$ values. The unit of time given is seconds. The statistical mean and standard deviation are the results after 5 experiments. It can be intuitively seen that in all data sets, the total time of feature extraction increases with the increase of prior parameter $K$. Among the four types of states, the longest time for comprehensive feature extraction is the rolling element fault, and the shortest is the outer ring fault. This indicates that the sensitivity of the outer circle fault diagnosis is faster. From Table 3 to Table 6, we can see that different training samples and test samples are respectively used for analysis of the four data sets. Combined with the recognition results in Fig. 6, we give the optimal prior parameter $K$ is 3 in Table 3, in data 1. Feature extraction takes 3.04 s. The optimal prior parameter $K$ in Table 4 and Table 5 is 6 in data sets 2 and 3. The total feature extraction time is 17.20 s and 23.15 s, respectively. The optimal prior parameter $K$ in Table 6 is 5, which is in data 4. The total feature extraction time takes 17.77 s. Table 7 shows the recognition results under different states when the extracted eigenvalues of energy entropy are directly classified in different data sets with different $K$ values. Table 7 lists the comparison results of predicted value labels and actual value labels of different test samples under four working conditions of motor rolling bearing. It can be seen from the results that among the four types of states, the sensitivity of the recognition effect of rolling element is the lowest. In Table 7, we also give the optimal prior parameter $K$ values in the 4 groups of data sets. From the classification and recognition results, to the influence of eigenvalues on the classification results, the construction of classifier network is also a key part to be considered in the diagnostic pattern system. In addition, to considering the classification performance of the recognition classification network, we also need to improve the performance of the sensitivity of the diagnostic mode system, that is, we need to consider the action time of the diagnostic system. The less time it takes to diagnose, the less likely there is to be economic loss and other damage caused by the failure of rotating machinery.

Fig. 6Different scheme identification results: a) data 1; b) data 2; c) data 3; d) data 4

a)

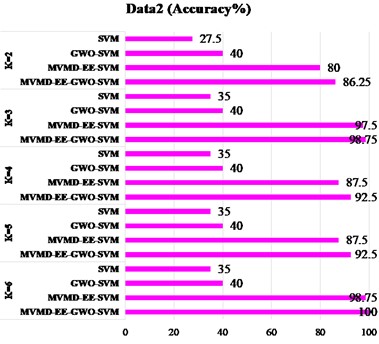
b)

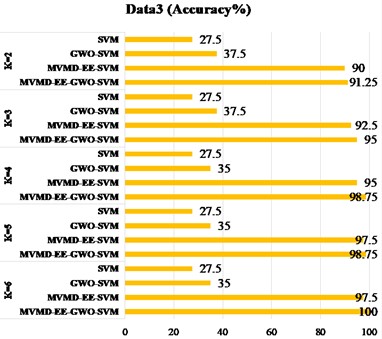
c)

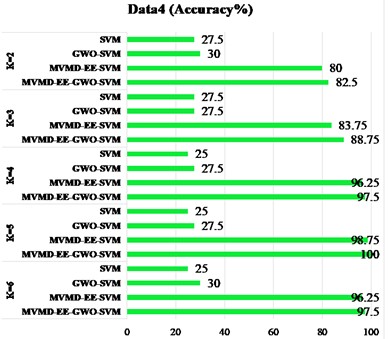
d)